如何用Python画各种著名数学图案

 

编译团队：Aileen  徐凌霄

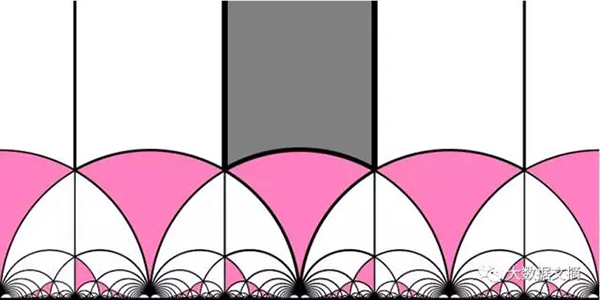
用Python绘制著名的数学图片或动画，展示数学中的算法魅力。

Mandelbrot 集

代码：46 lines (34 sloc) 1.01 KB

'''  
A fast Mandelbrot set wallpaper renderer 
 
  
reddit discussion: https://www.reddit.com/r/math/comments/2abwyt/smooth_colour_mandelbrot/  
'''  
import numpy as np  
from PIL import Image  
from numba import jit 
 
  
MAXITERS = 200 
RADIUS = 100 
 
  
@jit 
def color(z, i):  
v = np.log2(i + 1 - np.log2(np.log2(abs(z)))) / 5  
if v < 1.0: 
return v**4, v**2.5, v 
else:  
v = max(0, 2-v)  
return v, v**1.5, v**3 
 
  
@jit 
def iterate(c): 
z = 0j  
for i in range(MAXITERS):  
if z.real*z.real + z.imag*z.imag > RADIUS:  
return color(z, i) 
zz = z*z + c  
return 0, 0 ,0 
 
  
def main(xmin, xmax, ymin, ymax, width, height):  
x = np.linspace(xmin, xmax, width) 
y = np.linspace(ymax, ymin, height) 
z = x[None, :] + y[:, None]*1j 
red, green, blue = np.asarray(np.frompyfunc(iterate, 1, 3)(z)).astype(np.float) 
img = np.dstack((red, green, blue))  
Image.fromarray(np.uint8(img*255)).save('mandelbrot.png') 
 
  
if __name__ == '__main__':  
main(-2.1, 0.8, -1.16, 1.16, 1200, 960) 

多米诺洗牌算法

代码链接：https://github.com/neozhaoliang/pywonderland/tree/master/src/domino

正二十面体万花筒

代码：53 lines (40 sloc) 1.24 KB

''' 
A kaleidoscope pattern with icosahedral symmetry. 
''' 
import numpy as np 
from PIL import Image 
from matplotlib.colors import hsv_to_rgb 
 
  
def Klein(z): 
'''Klein's j-function'''  
return 1728 * (z * (z**10 + 11 * z**5 - 1))**5 / \ 
(-(z**20 + 1) + 228 * (z**15 - z**5) - 494 * z**10)**3 
 
  
def RiemannSphere(z):  
''' 
    map the complex plane to Riemann's sphere via stereographic projection 
    ''' 
t = 1 + z.real*z.real + z.imag*z.imag 
return 2*z.real/t, 2*z.imag/t, 2/t-1 
 
  
def Mobius(z): 
''' 
    distort the result image by a mobius transformation 
    ''' 
return (z - 20)/(3*z + 1j) 
 
  
def main(imgsize): 
x = np.linspace(-6, 6, imgsize))
y = np.linspace(6, -6, imgsize) 
z = x[None, :] + y[:, None]*1j 
z = RiemannSphere(Klein(Mobius(Klein(z)))) 
 
  
# define colors in hsv space 
H = np.sin(z[0]*np.pi)**2 
S = np.cos(z[1]*np.pi)**2 
V = abs(np.sin(z[2]*np.pi) * np.cos(z[2]*np.pi))**0.2 
HSV = np.dstack((H, S, V)) 
 
  
# transform to rgb space 
img = hsv_to_rgb(HSV)  
Image.fromarray(np.uint8(img*255)).save('kaleidoscope.png') 
 
  
if __name__ == '__main__':  
import time  
start = time.time()  
main(imgsize=800) 
end = time.time() 
print('runtime: {:3f} seconds'.format(end - 

Newton 迭代分形

代码：46 lines (35 sloc) 1.05 KB

import numpy as np 
import matplotlib.pyplot as plt 
from numba import jit 
 
  
# define functions manually, do not use numpy's poly1d funciton! 
@jit('complex64(complex64)', nopython=True)  
def f(z):  
# z*z*z is faster than z**3 
return z*z*z - 1 
 
  
@jit('complex64(complex64)', nopython=True) 
def df(z):  
return 3*z*z 
 
  
@jit('float64(complex64)', nopython=True)  
def iterate(z):  
num = 0  
while abs(f(z)) > 1e-4:  
w = z - f(z)/df(z)  
num += np.exp(-1/abs(w-z)) 
z = w 
return num 
 
  
def render(imgsize):  
x = np.linspace(-1, 1, imgsize)  
y = np.linspace(1, -1, imgsize)  
z = x[None, :] + y[:, None] * 1j  
img = np.frompyfunc(iterate, 1, 1)(z).astype(np.float) 
fig = plt.figure(figsize=(imgsize/100.0, imgsize/100.0), dpi=100) 
ax = fig.add_axes([0, 0, 1, 1], aspect=1) 
ax.axis('off') 
ax.imshow(img, cmap='hot'))
fig.savefig('newton.png') 
 
  
if __name__ == '__main__': 
import time  
start = time.time() 
render(imgsize=400) 
end = time.time()  
print('runtime: {:03f} seconds'.format(end  

李代数E8 的根系

代码链接：https://github.com/neozhaoliang/pywonderland/blob/master/src/misc/e8.py

模群的基本域

代码链接：

https://github.com/neozhaoliang/pywonderland/blob/master/src/misc/modulargroup.py

彭罗斯铺砌

代码链接：

https://github.com/neozhaoliang/pywonderland/blob/master/src/misc/penrose.py

Wilson 算法

代码链接：https://github.com/neozhaoliang/pywonderland/tree/master/src/wilson

反应扩散方程模拟

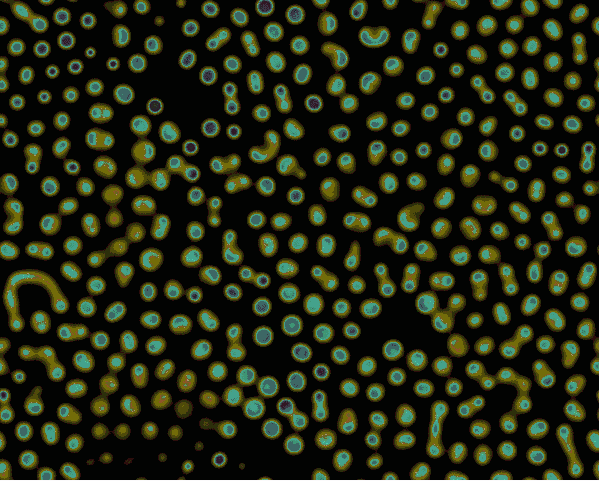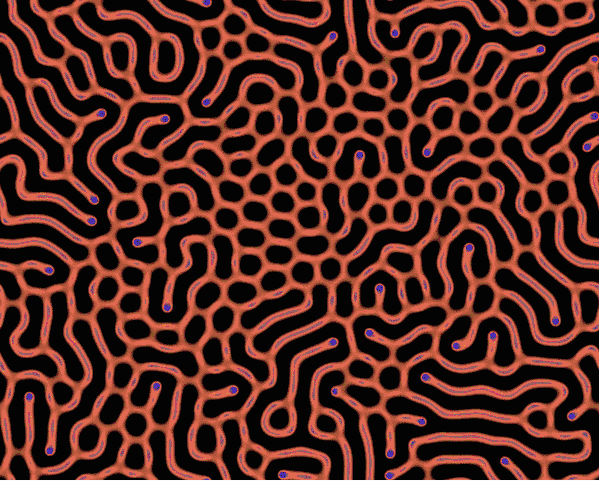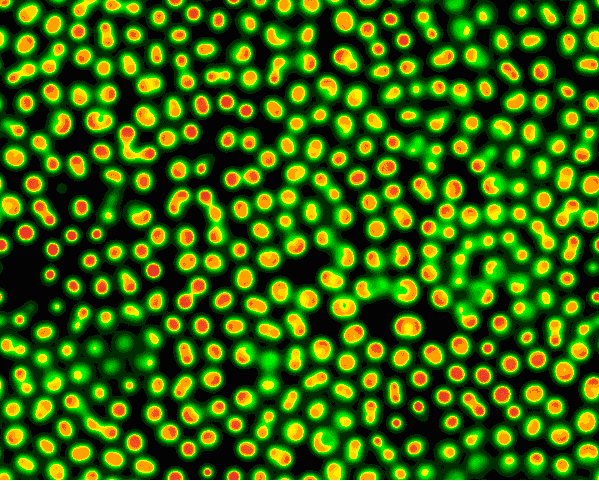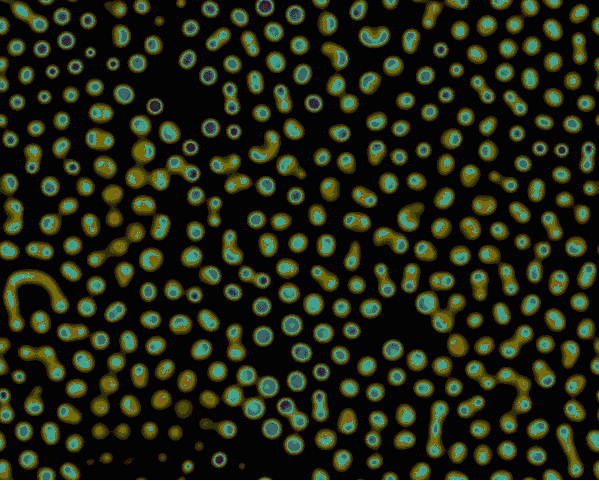
代码链接：https://github.com/neozhaoliang/pywonderland/tree/master/src/grayscott

120 胞腔

 

# pylint: disable=unused-import 
# pylint: disable=undefined-variable 
  
from itertools import combinations, product 
import numpy as np  
from vapory import * 
 
 
class Penrose(object): 
  
GRIDS = [np.exp(2j * np.pi * i / 5) for i in range(5)] 
  
def __init__(self, num_lines, shift, thin_color, fat_color, **config):  
self.num_lines = num_lines 
self.shift = shift 
self.thin_color = thin_color 
self.fat_color = fat_color 
selfself.objs = self.compute_pov_objs(**config) 
 
 
def compute_pov_objs(self, **config): 
objects_pool = [] 
  
for rhombi, color in self.tile(): 
p1, p2, p3, p4 = rhombi 
polygon = Polygon(5, p1, p2, p3, p4, p1,  
Texture(Pigment('color', color), config['default'])) 
objects_pool.append(polygon) 
  
for p, q in zip(rhombi, [p2, p3, p4, p1]): 
cylinder = Cylinder(p, q, config['edge_thickness'], config['edge_texture']) 
objects_pool.append(cylinder) 
  
for point in rhombi:  
x, y = point  
sphere = Sphere((x, y, 0), config['vertex_size'], config['vertex_texture']) 
objects_pool.append(sphere) 
  
return Object(Union(*objects_pool)) 
 
  
def rhombus(self, r, s, kr, ks): 
if (s - r)**2 % 5 == 1: 
color = self.thin_color 
else: 
color = self.fat_color 
  
point = (Penrose.GRIDS[r] * (ks - self.shift[s]) 
- Penrose.GRIDS[s] * (kr - self.shift[r])) *1j / Penrose.GRIDS[s-r].imag 
index = [np.ceil((point/grid).real + shift) 
for grid, shift in zip(Penrose.GRIDS, self.shift)] 
  
vertices = [] 
for index[r], index[s] in [(kr, ks), (kr+1, ks), (kr+1, ks+1), (kr, ks+1)]: 
vertices.append(np.dot(index, Penrose.GRIDS)) 
  
vertices_real = [(z.real, z.imag) for z in vertices] 
return vertices_real, color 
 
  
def tile(self): 
for r, s in combinations(range(5), 2): 
for kr, ks in product(range(-self.num_lines, self.num_lines+1), repeat=2): 
yield self.rhombus(r, s, kr, ks) 
 
  
def put_objs(self, *args): 
return Object(self.objs, *args) 

原文：https://github.com/neozhaoliang/pywonderland/blob/master/README.md

【本文是51CTO专栏机构大数据文摘的原创译文，微信公众号“大数据文摘（ id: BigDataDigest）”】

     

 

戳这里，看该作者更多好文