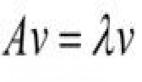机器学习的数学 之python矩阵运算

[[188138]]

本文提纲

1. 什么是矩阵

2. 矩阵在现实应用场景

3. 矩阵表示

4. 矩阵运算

5. 理解矩阵乘法

一、 什么是矩阵

一个 m × n 的矩阵是一个由 m 行 n 列元素排列成的矩形阵列。以下是一个由 6 个数字元素构成的 2 行 3 列的矩阵：

矩阵属于线性代数数学分支。线性代数是关于向量空间和线性映射的一个数学分支。它包括对线、面和子空间的研究，同时也涉及到所有的向量空间的一般性质。表面上，排成矩形的数字就是个矩阵。实际，矩阵是有限维线性空间的线性变换的表示形式。它代表着空间到空间的映射。

二、 矩阵在现实应用场景

在程序中，配合矩阵模拟真实数据，并可以实现如下功能：二维图形变换、人脸变换、人脸识别、信息转换等。比如一张图片，简单的黑白图只有黑色和白色构成，是不是可以有 1 0 两个数值的二维矩阵来表示呢?自然，尤其在图像处理里面，图像信息是用二维矩阵数据。

矩阵分析，是一种方便的计算工具，可以以简单的形式表达复杂的信息。

三、 矩阵表达式

我们选择 Python 作为代码演示案例。利用的是 NumPy 库。什么是 NumPy?

NumPy 是一个基础科学的计算包，包含：

• 一个强大的N维数组对象
• sophisticated (broadcasting) functions
• tools for integrating C/C++ and Fortran code
• 有用的线性代数、傅立叶转换和随机数生成函数

在代码中，导入 numpy 函数。

比如下面展示 1 × 2 和 2 × 2 的矩阵。调用 shape 方法，可获取矩阵的大小。同样，numpy 方便了我们很多操作。可以直接创建全 0 矩阵、全 1 矩阵和单元矩阵。代码 matrix_exp.py 如下：

# -*- coding: utf-8 -*- 
 
# 导入 numpy 函数，以 np 开头 
import numpy as np 
 
if __name__ == '__main__': 
    mat1 = np.array([1, 3]) 
    mat1 = np.mat(mat1)  # 相当于 np.mat([1,3])， mat 函数将目标数据的类型转换为矩阵（matrix） 
    print mat1 
    # 1 行 2 列的矩阵（也称 1 * 2 矩阵） 
    # ==> [[1 3]] 
 
    print 
 
    mat2 = np.array([[1, 3], [3, 4]]) 
    mat2 = np.mat(mat2) 
    print mat2 
    # 2 * 2 矩阵 
    # ==> [[1 3] 
    # ==>  [3 4]] 
 
    # 获取矩阵的大小 
    print mat1.shape 
    print mat2.shape 
 
    print 
 
    mat3 = np.zeros((2, 3))  # 2 * 3 的全 0 矩阵 
    mat4 = np.ones((3, 2))   # 3 * 2 的全 1 矩阵 
    mat5 = np.identity(3)    # 3 * 3 的单元矩阵 
    mat6 = np.eye(3, 3, 0)   # eye(N, M=None, k=0, dtype=float) 对角线是 1 其余值为 0 的矩阵, k 指定对角线的位置 
    print mat3 
    print mat4 
    print mat5 
    print mat6 

右键，Run 可得到下面结果：

[[1 3]] 
[[1 3] 
 [3 4]] 
(1, 2) 
(2, 2) 
[[ 0.  0.  0.] 
 [ 0.  0.  0.]] 
[[ 1.  1.] 
 [ 1.  1.] 
 [ 1.  1.]] 
[[ 1.  0.  0.] 
 [ 0.  1.  0.] 
 [ 0.  0.  1.]] 
[[ 1.  0.  0.] 
 [ 0.  1.  0.] 
 [ 0.  0.  1.]] 

如上注解详细解释了方法的使用。

「提示」代码共享在 GitHub：https://github.com/JeffLi1993/robot-mumu

四、 矩阵运算

矩阵运算包括了加减乘除、转置、逆矩阵、行列式、矩阵的幂、伴随矩阵等。

矩阵加法、减法、数量乘法规则如下：(和向量的运算规则一样)

• -A = (-1)A
• A - B = A + (-B)
• 2A + 3B = (2A)+ (3B)

比如下面展示下 矩阵与矩阵相乘、矩阵求逆、转置矩阵及每行或每列求和的运算。代码 matrix_op.py 如下：

# -*- coding: utf-8 -*- 
 
# 导入 numpy 函数，以 np 开头 
import numpy as np 
 
if __name__ == '__main__': 
    # 矩阵相乘 
    mat1 = np.mat([1, 3]) 
    mat2 = np.mat([[3], [4]]) 
    mat3 = mat1 * mat2 
    print mat3 
    # 1 * 2 矩阵乘以 2 * 1 矩阵，得到 1 * 1 矩阵 
    # ==> [[15]] 
 
    print 
 
    # 矩阵求逆 
    mat4 = np.mat([[1, 0, 1], [0, 2, 1], [1, 1, 1]]) 
    mat5 = mat4.I  # I 对应 getI(self) ，返回可逆矩阵的逆 
    print mat5 
    # 矩阵的逆 
    # ==> [[-1. -1.  2.] 
    # ==>  [-1.  0.  1.] 
    # ==>  [ 2.  1. -2.]] 
 
    print 
 
    # 转置矩阵 
    mat6 = np.mat([[1, 1, 1], [0, 2, 1], [1, 1, 1]]) 
    mat7 = mat6.T  # I 对应 getT(self) ，返回矩阵的转置矩阵 
    print mat7 
    # 矩阵的转置矩阵 
    # ==> [[1 0 1] 
    # ==>  [1 2 1] 
    # ==>  [1 1 1]] 
 
    print 
 
    # 矩阵每一列的和 
    sum1 = mat6.sum(axis=0) 
    print sum1 
    # 矩阵每一行的和 
    sum2 = mat6.sum(axis=1) 
    print sum2 
    # 矩阵所有行列的总和 
    sum3 = sum(mat6[1, :]) 
    print sum3 
 
    print 
 
    # 矩阵与数组之间的转换 
    mat8 = np.mat([[1, 2, 3]]) 
    arr1 = np.array(mat8)  # 矩阵转换成数组 
    print arr1 
    arr2 = [1, 2, 3] 
    mat9 = np.mat(arr2)  # 数组转换成矩阵 
    print mat9 

右键，Run 可得到下面结果：

[[15]]  
[[-1. -1. 2.]  
[-1. 0. 1.]  
[ 2. 1. -2.]]  
[[1 0 1]  
[1 2 1]  
[1 1 1]]  
[[2 4 3]]  
[[3]  
[3]  
[3]]  
[[0 2 1]]  
[[1 2 3]]  
[[1 2 3]] 

五、 理解矩阵和向量乘法

从解多元方程组可以看出

【本文为51CTO专栏作者“李强强”的原创稿件，转载请通过51CTO联系作者获取授权】

戳这里，看该作者更多好文