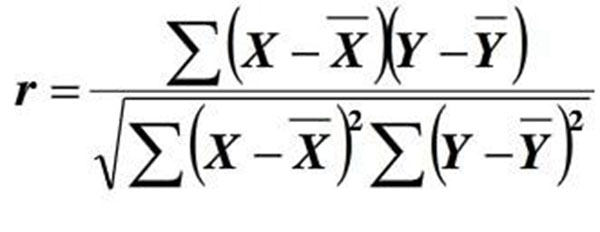很多时候我们走的走的就会忘记当初为什么而出发。
我们有的时候在拿到数据以后不知道该怎么进行分析,该去分析什么,其实这些在我们以前的统计学中都学过。
不管是用Python还是R,其实和用Excel一样,只不过现在之所以用Python、R是因为大数据时代么,数据太多,Excel的处理能力跟不上,但是这些都只是一个工具而已,核心还是围绕统计学不变的。
今天就来聊聊我们该从哪些方向去分析(描述)数据。
01 总规模度量:
总量指标又称统计绝对数,是反映某一数据的整体规模大小,总量多少的指标。他是对原始数据经管分组和汇总以后得到的各项总计数字,是统计整理阶段的直接成功。
比如泰坦尼克号数据中总共有891条乘客数据,其中有342是幸存者。
02 相对度量:
相对指标是说明现象之间数量对比关系的指标,由两个有联系的指标数值对比而求得,其结果表现为相对数,相对数的重要特点就是把两个具体的数值概括为一个抽象的数.
比如:泰坦尼克号数据中我们可以把存者数据和所有乘客数据的相比概括为为幸存率这么一个数。
相对数有有单位和无单位两种表现形式,在相对指标中,大多数都是以无单位的形式表示的,无单位是一种抽象化的数值,常以系数、倍数、百分数等表示;而有单位主要是用来表现强度相对指标的数值,比如人口密度:“人/平方公里”。
03 集中趋势的度量:
集中趋势是通过指标反映某一现象在一定时间段内所达到的一般水平。用平均指标来表示。平均指标分为数值平均和位置平均。
比如:泰坦尼克号数据中平均年龄和平均票价。
1、数值平均是统计数列中所有变量值平均的结果。有普通平均数和加权平均数两种。
2、位置平均时基于某种特殊位置上或者是普遍出现的标志值作为整体一般水平的代表值。有众数、中位数两种。
众数是被研究总体中出现次数最多的变量值,他是总体中最普遍的值,因此可以用来代表一般水平。如果数据可以分为多组,则为每组找出一个众数。注意:众数只有在总体内单位充分多时才有意义。
中位数是将总体中各单位标志值按大小顺序排列,处于中间位置的变量值就是中位数。因为处于中间位置,有一半变量值大于该值,一半小于该值,所以可以用这样的中等水平来表示整体的一般水平。
04 离散程度的度量:
变异指标是用来表示总体分布的变异情况和离散程度的指标,通过变异程度也可以看出平均值指标的代表性程度,如果离散程度小,说明大部分数据都是挨着的,则平均值可以很好的反映整体情况的一般水平,反之相反。
全距(又称极差)、方差、标准差等几个指标是用来衡量数值的分散性和变异性。
1、全距(极差):平均数让我们有办法确定一批数据的中心,但是无法知道数据的变动情况,所以引入全距,全距的计算方法是用数据集中***数(上界)减去数据集中最小数(下届)。
全距存在的问题:
- 容易受异常值影响。
- 全距只表示了数据的宽度,但是没有描述清楚数据上下界之间的分布形态。
2、对于***种问题我们引入四分位距的概念。四分位数将一些数值从小到大排列,然后一分为四,最小的四分位数为下四分位数,***的四分位数为上四分位数,中间的四分位数为中位数。
3、对于问题2我们引入了方差和标准差两个概念来度量数据的分散性。
- 方差是每个数值与均值距离的平方的平均值,方差越小说明各数值与均值之间的差距越小,数值越稳定。
- 标准差是方差的开方。表示数值与均值距离的平均值。
05 偏态与峰度的度量:
1、偏度是用来衡量统计分布的不对称程度或偏斜程度的指标,值越大,偏斜成度越大;值越小,偏斜成度越小。
2、峰度又称峰态系数。表征概率密度分布曲线在平均值处峰值高低的特征数。直观看来,峰度反映了峰部的尖度。值越大,越尖。
06 相关性度量:
上面提到的几个维度是对数据整体的情况进行描述,但是我们有的时候想看一下数据整体内的变量之间存在什么关系,一个变化时会引起另一个怎么变化,我们把用来反映这种关系的指标叫做相关系数。
(相关系数计算公式)
- 关于相关系数需要注意几点:
- 相关系数r的范围为:[-1,1]。
- r的绝对值越大,表示相关性越强。
r的正负代表相关性方向,正代表正相关,负代表负相关。