一、前言
用过暴力破解工具 hashcat 的都知道,这款软件的强大之处在于它能充分利用 GPU 计算,比起 CPU 要快很多。所以在破解诸如 WiFi 握手包、数据库中的口令 Hash 值时,能大幅提高计算效率。
当然 GPU 仍属于通用硬件,显然还不是最优化的。要是为特定的算法打造特定的硬件,效率更是高出几个量级。比特币矿机就是很好的例子。
硬件仍在不断进步,系统安全等级若不提高,暴力破解将会越来越容易。因此,一种能抵抗「硬件破解」的 Hash 算法,显得很有必要。
二、时间成本
在探讨如何对抗硬件之前,先来讲解过去是如何对抗「暴力破解」的。
一些经典的 Hash 算法,例如 MD5、SHA256 等,计算速度是非常快的。如果口令 Hash 用了这类函数,将来攻击者跑字典时,可达到非常高的速度。那些强度不高的口令,很容易被破解。
为了缓解这种状况,密码学家引入了「拉伸」的概念:反复 Hash 多次,从而增加计算时间。
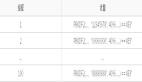
例如 PBKDF2 算法就运用了这种思想。它的原理很简单,对指定函数 F 反复进行 N 次:
- function PBKDF2(F, ..., N)
- ...
- for i = 0 to N
- ...
- x = F(x, ...)
- ...
- ...
- return x
这样就能灵活设定 Hash 的时间成本了。例如设定 10000,对开发者来说,只是多了几十毫秒的计算;但对于攻击者,破解速度就降低了一万倍!
1. 时间成本局限性
PBKDF2 确实有很大的效果,但对于硬件破解,却无任何对抗措施。
因为 PBKDF2 只是对原函数简单封装,多执行几次而已。如果原函数不能对抗硬件,那么套一层 PBKDF2 同样也不能。
例如 WiFi 的 WPA2 协议,就是让 HMAC-SHA1 重复执行 4096 次:
- DK = PBKDF2(HMAC−SHA1, Password, SSID, 4096, ...)
虽然相比单次 Hash 要慢上几千倍,但这并不妨碍硬件破解。
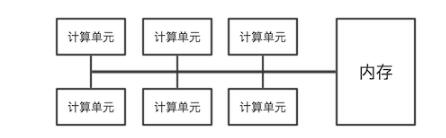
硬件依然可发挥其「高并发」优势,让每个线程分别计算不同口令的 PBKDF2:
虽然耗时确实增加了很多倍,但并没有影响到硬件的发挥。同样的破解,效率仍然远高于 CPU。
所以,时间成本并不能抵抗「硬件破解」。
2. 空间成本
单论计算性能,硬件是非常逆天的,但再综合一些其他因素,或许就未必那么强大了。
假如某个硬件可开启 100 个线程同时破解,但总内存却只有 100M —— 这显然是个很大的短板。
如果有种 PBKDF 算法空间复杂度为 2M,那将会有一半的线程,因内存不足而无法运行!
若再极端些,将空间复杂度提高到 100M,那么整个硬件只能开启 1 个线程,99% 的算力都无法得到发挥!
这样,即使硬件的计算性能再强劲,也终将卡在内存这个瓶颈上。
不过,怎样才能让算法消耗这么多内存,同时又不能被轻易绕过?这里举个简单的例子:
- function MemoryHard(..., M)
- int space[M]
- for i = 0 .. 10000
- x = Hash(x, ...)
- space[int(x) % M] ^= int(x)
- return Hash(space)
当然这个例子是随意写的,并不严谨。但主要思想是:
- 引入了空间成本 M,并申请相应的内存
- 利用经典 Hash 函数的结果,作为数组索引,对内存进行读写
- 每次内存读写,都会影响到最终结果
由于 Hash 函数的结果是不可预测的,因此事先无法知道哪些位置会被访问。只有准备充足的内存,才能达到 O(1) 的访问速度。
攻击者要想达到同样的速度,就不得不花费同样多的内存!
3. 时空权衡
通常硬件的「计算资源」要比「存储资源」充足得多,因此可考虑「时间换空间」的策略 —— 使用更复杂的存储管理机制,从而减少空间分配,这样就能开启更多的线程。
比如牺牲 40% 的速度,换取 50% 的空间:
由于空间成本是之前的一半,因此可多启动一倍的线程。算上折损,最终速度仍增加了 20%。
当然,如果 性能折损比例 > 空间压缩比例,这个方案就没有意义了。
4. 访问瓶颈
事实上,内存除了容量外,访问频率也是有限制的。
就内存本身而言,每秒读写次数是有上限的。其次,计算单元和内存之间的交互,更是一大瓶颈。
像 MD5、SHA256 这类 Hash 函数,空间复杂度非常低。硬件破解时,每个计算单元光靠自身的寄存器以及高速缓存,就差不多够用了,很少需要访问内存。
但对于 Memory-Hard 函数,就没那么顺利了。它不仅很占内存,而且还十分频繁地「随机访问」内存,因此很难命中高速缓存。这使得每次访问,几乎都会和内存进行交互,从而占用大量带宽。
如果有多个计算单元频繁访问,那么内存带宽就会成为瓶颈。这样,也能起到抑制并发的效果!
例如 bcrypt 算法就运用了类似思想,它在计算过程中频繁访问 4KB 的内存空间,从而消耗带宽资源。
不过随着硬件发展,bcrypt 的优势也在逐渐降低。为了能更灵活地设定内存大小,scrypt 算法出现了 —— 它既有时间成本,还有空间成本,这样就能更持久地对抗。
当然,空间成本也不是绝对有效的。如果攻击者不惜代价,制造出存储「容量」和「带宽」都很充足的硬件设备,那么仍能高效地进行破解。
三、并行维度
十几年来,内存容量翻了好几翻,但 CPU 主频却没有很大提升。由于受到物理因素的制约,主频已很难提升,只能朝着多核发展。
然而像 PBKDF2 这样的算法,却只能使用单线程计算 —— 因为它每次 Hash 都依赖上一次的 Hash 结果。这种串行的模式,是无法拆解成多个任务的,也就无法享受多线程的优势。
这就意味着 —— 时间成本,终将达到一个瓶颈!
对此,多线程真的无能为力吗?
尽管单次 PBKDF 不能被拆解,但可以要求多次 PBKDF,并且互相没有依赖。这样多线程就能派上用场了。
例如我们对 PBKDF 进行封装,要求执行 4 次完全独立的计算,最后再将结果融合到一起:
- function Parall(Password, Salt, ...)
- -- 该部分可被并行 --
- for i = 0 .. 4
- DK[i] = PBKDF(Password, Salt + i, ...)
- ------------------
- return Hash(DK)
这样,我们即可开启 4 个线程,同时计算这 4 个 PBKDF。
现在就能用 1 秒的时间,获得之前 4 秒的强度!攻击者破解时,成本就增加了 4 倍。
如今主流的口令 Hash 函数都支持「并行维度」。例如 scrypt 以及更先进的 argon2,都可通过参数 p 设定。
1. 线程开销
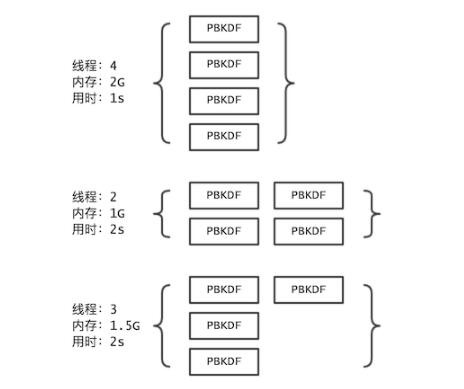
现实中,「线程数」未必要和「并行维度」一样多,因为还得考虑「空间成本」。
假设上述的 PBKDF 空间成本有 512MB,如果开启 4 个线程,就得占用 2GB 的内存!若用户只有 1.5 GB 的空闲内存,还不如只开 2 个线程,反而会更顺畅。
当然,也可以开 3 个线程,但这样会更快吗?显然不会!
因为 4 个任务分给 3 个线程,总有一个线程得做两份,所以最终用时并没有缩短。反而增加了线程创建、内存申请等开销。
这里有个 scrypt 算法在线演示:https://etherdream.github.io/webscrypt/example/basic/
大家可体会下 时空成本(N)、并行维度(P)、线程数(Thread)对计算的影响。
四、小结
到此,我们讲解了 3 个对抗破解的因素:
- 时间成本(迭代次数)
- 空间成本(内存容量、带宽)
- 并行维度(多线程资源)
或许你已感悟到这其中的理念 —— 让 Hash 算法牵涉更多的硬件能力。这样,只有综合性能高的硬件,才能顺利运行;专为某个功能打造的硬件,就会出现瓶颈!
照这个思路,我们也可发挥想象:假如有个算法使用了不少条件分支指令,而 CPU 正好拥有强大的分支预测功能。这样该算法在 CPU 上运行时,就能获得很高的性能;而在其他精简过的硬件上,就没有这么好的效果了。
当然这里纯属想象,自创密码学算法是不推荐的。现实中还是得用更权威的算法,例如 argon2、scrypt 等。
五、应用
本文提到的对抗方案,都是从硬件消耗上进行的。不过,这样伤敌一千也会自损八百。
假如服务器每 Hash 一次口令,就得花 1 秒时间加 1GB 内存,那么一旦有几十个人同时访问,系统可能就支撑不住了。
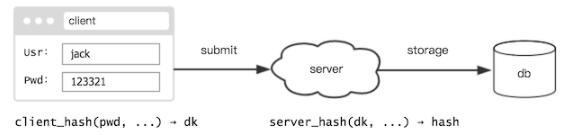
有什么办法,既能使用高成本的 Hash,又不耗费服务器资源?事实上,口令 Hash 完全可以在客户端计算:
- DK = Client_PBKDF(Password, Username, Cost ...)
因为口令与 DK 的对应关系是唯一的。账号注册时,提交的就是 DK;登录时,如果提交的 DK 相同,也就证明口令是相同的。
所以客户端无需提供原始口令,服务端也能认证,这就是「零知识证明」。使用这种方案,还能进一步减少口令泄露的环节,例如网络被窃听、服务端恶意程序等。
当然,服务端收到 DK 后,还不能立即存储。因为万一 DK 泄露了,攻击者还是能用它登上用户的账号 —— 尽管不知道口令。
因此,服务端需对 DK 再进行 Hash 处理。
不过这一次,只需快速的 Hash 函数即可。因为 DK 是无规律的数据(熵很高),无法通过跑字典还原,所以用简单的 Hash 就能保护。
这样,服务器只需极小的计算开销,就能实现高强度的口令安全了!
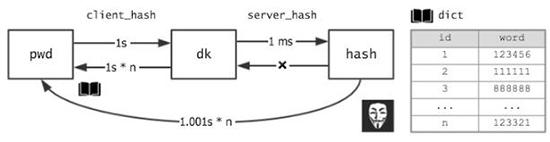
将来即使被拖库,攻击者也只能使用如下 Hash 函数跑字典:
- f(x) => server_hash( client_hash(x) )
因为其中用到了 client_hash,所以这个最终函数同样能对抗硬件破解!