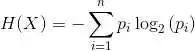决策树算法是一个强大的预测方法,它非常流行。因为它们的模型能够让新手轻而易举地理解得和专家一样好,所以它们比较流行。同时,最终生成的决策树能够解释做出特定预测的确切原因,这使它们在实际运用中倍受亲睐。
同时,决策树算法也为更高级的集成模型(如 bagging、随机森林及 gradient boosting)提供了基础。
在这篇教程中,你将会从零开始,学习如何用 Python 实现《Classification And Regression Tree algorithm》中所说的内容。
在学完该教程之后,你将会知道:
如何计算并评价数据集中地候选分割点(Candidate Split Point)
如何在决策树结构中排分配这些分割点
如何在实际问题中应用这些分类和回归算法
一、概要
本节简要介绍了关于分类及回归树(Classification and Regression Trees)算法的一些内容,并给出了将在本教程中使用的钞票数据集(Banknote Dataset)。
1.1 分类及回归树
分类及回归树(CART)是由 Leo Breiman 提出的一个术语,用来描述一种能被用于分类或者回归预测模型问题的回归树算法。
我们将在本教程中主要讨论 CART 在分类问题上的应用。
二叉树(Binary Tree)是 CART 模型的代表之一。这里所说的二叉树,与数据结构和算法里面所说的二叉树别无二致,没有什么特别之处(每个节点可以有 0、1 或 2 个子节点)。
每个节点代表在节点处有一个输入变量被传入,并根据某些变量被分类(我们假定该变量是数值型的)。树的叶节点(又叫做终端节点,Terminal Node)由输出变量构成,它被用于进行预测。
在树被创建完成之后,每个新的数据样本都将按照每个节点的分割条件,沿着该树从顶部往下,直到输出一个最终决策。
创建一个二元分类树实际上是一个分割输入空间的过程。递归二元分类(Recursive Binary Splitting)是一个被用于分割空间的贪心算法。这实际上是一个数值过程:当一系列的输入值被排列好后,它将尝试一系列的分割点,测试它们分类完后成本函数(Cost Function)的值。
有最优成本函数(通常是最小的成本函数,因为我们往往希望该值最小)的分割点将会被选择。根据贪心法(greedy approach)原则,所有的输入变量和所有可能的分割点都将被测试,并会基于它们成本函数的表现被评估。(译者注:下面简述对回归问题和分类问题常用的成本函数。)
- 回归问题:对落在分割点确定区域内所有的样本取误差平方和(Sum Squared Error)。
- 分类问题:一般采用基尼成本函数(Gini Cost Function),它能够表明被分割之后每个节点的纯净度(Node Purity)如何。其中,节点纯净度是一种表明每个节点分类后训练数据混杂程度的指标。
分割将一直进行,直到每个节点(分类后)都只含有最小数量的训练样本或者树的深度达到了最大值。
1.2 Banknote 数据集
Banknote 数据集,需要我们根据对纸币照片某些性质的分析,来预测该钞票的真伪。
该数据集中含有 1372 个样本,每个样本由 5 个数值型变量构成。这是一个二元分类问题。如下列举 5 个变量的含义及数据性质:
1. 图像经小波变换后的方差(Variance)(连续值)
2. 图像经小波变换后的偏度(Skewness)(连续值)
3. 图像经小波变换后的峰度(Kurtosis)(连续值)
4. 图像的熵(Entropy)(连续值)
5. 钞票所属类别(整数,离散值)
如下是数据集前五行数据的样本。
3.6216,8.6661,-2.8073,-0.44699,0
4.5459,8.1674,-2.4586,-1.4621,0
3.866,-2.6383,1.9242,0.10645,0
3.4566,9.5228,-4.0112,-3.5944,0
0.32924,-4.4552,4.5718,-0.9888,0
4.3684,9.6718,-3.9606,-3.1625,0
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
使用零规则算法(Zero Rule Algorithm)来预测最常出现类别的情况(译者注:也就是找到最常出现的一类样本,然后预测所有的样本都是这个类别),对该问的基准准确大概是 50%。
你可以在这里下载并了解更多关于这个数据集的内容:UCI Machine Learning Repository。
请下载该数据集,放到你当前的工作目录,并重命名该文件为 data_banknote_authentication.csv。
二、教程
本教程分为五大部分:
1. 对基尼系数(Gini Index)的介绍
2.(如何)创建分割点
3.(如何)生成树模型
4.(如何)利用模型进行预测
5. 对钞票数据集的案例研究
这些步骤能帮你打好基础,让你能够从零实现 CART 算法,并能将它应用到你子集的预测模型问题中。
2.1 基尼系数
基尼系数是一种评估数据集分割点优劣的成本函数。
数据集的分割点是关于输入中某个属性的分割。对数据集中某个样本而言,分割点会根据某阈值对该样本对应属性的值进行分类。他能根据训练集中出现的模式将数据分为两类。
基尼系数通过计算分割点创建的两个类别中数据类别的混杂程度,来表现分割点的好坏。一个完美的分割点对应的基尼系数为 0(译者注:即在一类中不会出现另一类的数据,每个类都是「纯」的),而最差的分割点的基尼系数则为 1.0(对于二分问题,每一类中出现另一类数据的比例都为 50%,也就是数据完全没能被根据类别不同区分开)。
下面我们通过一个具体的例子来说明如何计算基尼系数。
我们有两组数据,每组有两行。第一组数据中所有行都属于类别 0(Class 0),第二组数据中所有的行都属于类别 1(Class 1)。这是一个完美的分割点。
首先我们要按照下式计算每组数据中各类别数据的比例:
proportion = count(class_value) / count(rows)
- 1.
那么,对本例而言,相应的比例为:
group_1_class_0 = 2 / 2 = 1
group_1_class_1 = 0 / 2 = 0
group_2_class_0 = 0 / 2 = 0
group_2_class_1 = 2 / 2 = 1
- 1.
- 2.
- 3.
- 4.
基尼系数按照如下公式计算:
gini_index = sum(proportion * (1.0 - proportion))
- 1.
将本例中所有组、所有类数据的比例带入到上述公式:
gini_index = (group_1_class_0 * (1.0 - group_1_class_0)) +
(group_1_class_1 * (1.0 - group_1_class_1)) +
(group_2_class_0 * (1.0 - group_2_class_0)) +
(group_2_class_1 * (1.0 - group_2_class_1))
- 1.
- 2.
- 3.
- 4.
化简,得:
gini_index = 0 + 0 + 0 + 0 = 0
- 1.
如下是一个叫做 gini_index() 的函数,它能够计算给定数据的基尼系数(组、类别都以列表(list)的形式给出)。其中有些算法鲁棒性检测,能够避免对空组除以 0 的情况。
# Calculate the Gini index for a split dataset
def gini_index(groups, class_values):
gini = 0.0
for class_value in class_values:
for group in groups:
size = len(group)
if size == 0:
continue
proportion = [row[-1] for row in group].count(class_value) / float(size)
gini += (proportion * (1.0 - proportion))
return gini
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
我们可以根据上例来测试该函数的运行情况,也可以测试最差分割点的情况。完整的代码如下:
# Calculate the Gini index for a split dataset
def gini_index(groups, class_values):
gini = 0.0
for class_value in class_values:
for group in groups:
size = len(group)
if size == 0:
continue
proportion = [row[-1] for row in group].count(class_value) / float(size)
gini += (proportion * (1.0 - proportion))
return gini
# test Gini values
print(gini_index([[[1, 1], [1, 0]], [[1, 1], [1, 0]]], [0, 1]))
print(gini_index([[[1, 0], [1, 0]], [[1, 1], [1, 1]]], [0, 1]))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
运行该代码,将会打印两个基尼系数,其中第一个对应的是最差的情况为 1.0,第二个对应的是最好的情况为 0.0。
1.0
0.0
- 1.
- 2.
2.2 创建分割点
一个分割点由数据集中的一个属性和一个阈值构成。
我们可以将其总结为对给定的属性确定一个分割数据的阈值。这是一种行之有效的分类数据的方法。
创建分割点包括三个步骤,其中第一步已在计算基尼系数的部分讨论过。余下两部分分别为:
1. 分割数据集。
2. 评价所有(可行的)分割点。
我们具体看一下每个步骤。
2.2.1 分割数据集
分割数据集意味着我们给定数据集某属性(或其位于属性列表中的下表)及相应阈值的情况下,将数据集分为两个部分。
一旦数据被分为两部分,我们就可以使用基尼系数来评估该分割的成本函数。
分割数据集需要对每行数据进行迭代,根据每个数据点相应属性的值与阈值的大小情况将该数据点放到相应的部分(对应树结构中的左叉与右叉)。
如下是一个名为 test_split() 的函数,它能实现上述功能:
# Split a dataset based on an attribute and an attribute value
def test_split(index, value, dataset):
left, right = list(), list()
for row in dataset:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left, right
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
代码还是很简单的。
注意,在代码中,属性值大于或等于阈值的数据点被分类到了右组中。
2.2.2 评价所有分割点
在基尼函数 gini_index() 和分类函数 test_split() 的帮助下,我们可以开始进行评估分割点的流程。
对给定的数据集,对每一个属性,我们都要检查所有的可能的阈值使之作为候选分割点。然后,我们将根据这些分割点的成本(cost)对其进行评估,最终挑选出最优的分割点。
当最优分割点被找到之后,我们就能用它作为我们决策树中的一个节点。
而这也就是所谓的穷举型贪心算法。
在该例中,我们将使用一个词典来代表决策树中的一个节点,它能够按照变量名储存数据。当选择了最优分割点并使用它作为树的新节点时,我们存下对应属性的下标、对应分割值及根据分割值分割后的两部分数据。
分割后地每一组数据都是一个更小规模地数据集(可以继续进行分割操作),它实际上就是原始数据集中地数据按照分割点被分到了左叉或右叉的数据集。你可以想象我们可以进一步将每一组数据再分割,不断循环直到建构出整个决策树。
如下是一个名为 get_split() 的函数,它能实现上述的步骤。你会发现,它遍历了每一个属性(除了类别值)以及属性对应的每一个值,在每次迭代中它都会分割数据并评估该分割点。
当所有的检查完成后,最优的分割点将被记录并返回。
# Select the best split point for a dataset
def get_split(dataset):
class_values = list(set(row[-1] for row in dataset))
b_index, b_value, b_score, b_groups = 999, 999, 999, None
for index in range(len(dataset[0])-1):
for row in dataset:
groups = test_split(index, row[index], dataset)
gini = gini_index(groups, class_values)
if gini < b_score:
b_index, b_value, b_score, b_groups = index, row[index], gini, groups
return {'index':b_index, 'value':b_value, 'groups':b_groups}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
我们能在一个小型合成的数据集上来测试这个函数以及整个数据集分割的过程。
X1 X2 Y
2.771244718 1.784783929 0
1.728571309 1.169761413 0
3.678319846 2.81281357 0
3.961043357 2.61995032 0
2.999208922 2.209014212 0
7.497545867 3.162953546 1
9.00220326 3.339047188 1
7.444542326 0.476683375 1
10.12493903 3.234550982 1
6.642287351 3.319983761 1
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
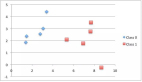
同时,我们可以使用不同颜色标记不同的类,将该数据集绘制出来。由图可知,我们可以从 X1 轴(即图中的 X 轴)上挑出一个值来分割该数据集。
范例所有的代码整合如下:
# Split a dataset based on an attribute and an attribute value
def test_split(index, value, dataset):
left, right = list(), list()
for row in dataset:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left, right
# Calculate the Gini index for a split dataset
def gini_index(groups, class_values):
gini = 0.0
for class_value in class_values:
for group in groups:
size = len(group)
if size == 0:
continue
proportion = [row[-1] for row in group].count(class_value) / float(size)
gini += (proportion * (1.0 - proportion))
return gini
# Select the best split point for a dataset
def get_split(dataset):
class_values = list(set(row[-1] for row in dataset))
b_index, b_value, b_score, b_groups = 999, 999, 999, None
for index in range(len(dataset[0])-1):
for row in dataset:
groups = test_split(index, row[index], dataset)
gini = gini_index(groups, class_values)
print('X%d < %.3f Gini=%.3f' % ((index+1), row[index], gini))
if gini < b_score:
b_index, b_value, b_score, b_groups = index, row[index], gini, groups
return {'index':b_index, 'value':b_value, 'groups':b_groups}
dataset = [[2.771244718,1.784783929,0],
[1.728571309,1.169761413,0],
[3.678319846,2.81281357,0],
[3.961043357,2.61995032,0],
[2.999208922,2.209014212,0],
[7.497545867,3.162953546,1],
[9.00220326,3.339047188,1],
[7.444542326,0.476683375,1],
[10.12493903,3.234550982,1],
[6.642287351,3.319983761,1]]
split = get_split(dataset)
print('Split: [X%d < %.3f]' % ((split['index']+1), split['value']))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
优化后的 get_split() 函数能够输出每个分割点及其对应的基尼系数。
运行如上的代码后,它将 print 所有的基尼系数及其选中的最优分割点。在此范例中,它选中了 X1<6.642 作为最终完美分割点(它对应的基尼系数为 0)。
X1 < 2.771 Gini=0.494
X1 < 1.729 Gini=0.500
X1 < 3.678 Gini=0.408
X1 < 3.961 Gini=0.278
X1 < 2.999 Gini=0.469
X1 < 7.498 Gini=0.408
X1 < 9.002 Gini=0.469
X1 < 7.445 Gini=0.278
X1 < 10.125 Gini=0.494
X1 < 6.642 Gini=0.000
X2 < 1.785 Gini=1.000
X2 < 1.170 Gini=0.494
X2 < 2.813 Gini=0.640
X2 < 2.620 Gini=0.819
X2 < 2.209 Gini=0.934
X2 < 3.163 Gini=0.278
X2 < 3.339 Gini=0.494
X2 < 0.477 Gini=0.500
X2 < 3.235 Gini=0.408
X2 < 3.320 Gini=0.469
Split: [X1 < 6.642]
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
既然我们现在已经能够找出数据集中最优的分割点,那我们现在就来看看我们能如何应用它来建立一个决策树。
2.3 生成树模型
创建树的根节点(root node)是比较方便的,可以调用 get_split() 函数并传入整个数据集即可达到此目的。但向树中增加更多的节点则比较有趣。
建立树结构主要分为三个步骤:
1. 创建终端节点
2. 递归地分割
3. 建构整棵树
2.3.1 创建终端节点
我们需要决定何时停止树的「增长」。
我们可以用两个条件进行控制:树的深度和每个节点分割后的数据点个数。
最大树深度:这代表了树中从根结点算起节点数目的上限。一旦树中的节点树达到了这一上界,则算法将会停止分割数据、增加新的节点。更神的树会更为复杂,也更有可能过拟合训练集。
最小节点记录数:这是某节点分割数据后分个部分数据个数的最小值。一旦达到或低于该最小值,则算法将会停止分割数据、增加新的节点。将数据集分为只有很少数据点的两个部分的分割节点被认为太具针对性,并很有可能过拟合训练集。
这两个方法基于用户给定的参数,参与到树模型的构建过程中。
此外,还有一个情况。算法有可能选择一个分割点,分割数据后所有的数据都被分割到同一组内(也就是左叉、右叉只有一个分支上有数据,另一个分支没有)。在这样的情况下,因为在树的另一个分叉没有数据,我们不能继续我们的分割与添加节点的工作。
基于上述内容,我们已经有一些停止树「增长」的判别机制。当树在某一结点停止增长的时候,该节点被称为终端节点,并被用来进行最终预测。
预测的过程是通过选择组表征值进行的。当遍历树进入到最终节点分割后的数据组中,算法将会选择该组中最普遍出现的值作为预测值。
如下是一个名为 to_terminal() 的函数,对每一组收据它都能选择一个表征值。他能够返回一系列数据点中最普遍出现的值。
# Create a terminal node value
def to_terminal(group):
outcomes = [row[-1] for row in group]
return max(set(outcomes), key=outcomes.count)
- 1.
- 2.
- 3.
- 4.
2.3.2 递归分割
在了解了如何及何时创建终端节点后,我们现在可以开始建立树模型了。
建立树地模型,需要我们对给定的数据集反复调用如上定义的 get_split() 函数,不断创建树中的节点。
在已有节点下加入的新节点叫做子节点。对树中的任意节点而言,它可能没有子节点(则该节点为终端节点)、一个子节点(则该节点能够直接进行预测)或两个子节点。在程序中,在表示某节点的字典中,我们将一棵树的两子节点命名为 left 和 right。
一旦一个节点被创建,我们就可以递归地对在该节点被分割得到的两个子数据集上调用相同的函数,来分割子数据集并创建新的节点。
如下是一个实现该递归过程的函数。它的输入参数包括:某一节点(node)、最大树深度(max_depth)、最小节点记录数(min_size)及当前树深度(depth)。
显然,一开始运行该函数时,根节点将被传入,当前深度为 1。函数的功能分为如下几步:
1. 首先,该节点分割的两部分数据将被提取出来以便使用,同时数据将被在节点中删除(随着分割工作的逐步进行,之前的节点不需要再使用相应的数据)。
2. 然后,我们将会检查该节点的左叉及右叉的数据集是否为空。如果是,则其将会创建一个终端节点。
3. 同时,我们会检查是否到达了最大深度。如果是,则其将会创建一个终端节点。
4. 接着,我们将对左子节点进一步操作。若该组数据个数小于阈值,则会创建一个终端节点并停止进一步操作。否则它将会以一种深度优先的方式创建并添加节点,直到该分叉达到底部。
5. 对右子节点同样进行上述操作,不断增加节点直到达到终端节点。
2.3.3 建构整棵树
我们将所有的内容整合到一起。
创建一棵树包括创建根节点及递归地调用 split() 函数来不断地分割数据以构建整棵树。
如下是实现上述功能的 bulid_tree() 函数的简化版本。
# Build a decision tree
def build_tree(train, max_depth, min_size):
root = get_split(dataset)
split(root, max_depth, min_size, 1)
return root
- 1.
- 2.
- 3.
- 4.
- 5.
我们可以在如上所述的合成数据集上测试整个过程。如下是完整的案例。
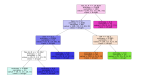
在其中还包括了一个 print_tree() 函数,它能够递归地一行一个地打印出决策树的节点。经过它打印的不是一个明显的树结构,但它能给我们关于树结构的大致印象,并能帮助决策。
# Split a dataset based on an attribute and an attribute value
def test_split(index, value, dataset):
left, right = list(), list()
for row in dataset:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left, right
# Calculate the Gini index for a split dataset
def gini_index(groups, class_values):
gini = 0.0
for class_value in class_values:
for group in groups:
size = len(group)
if size == 0:
continue
proportion = [row[-1] for row in group].count(class_value) / float(size)
gini += (proportion * (1.0 - proportion))
return gini
# Select the best split point for a dataset
def get_split(dataset):
class_values = list(set(row[-1] for row in dataset))
b_index, b_value, b_score, b_groups = 999, 999, 999, None
for index in range(len(dataset[0])-1):
for row in dataset:
groups = test_split(index, row[index], dataset)
gini = gini_index(groups, class_values)
if gini < b_score:
b_index, b_value, b_score, b_groups = index, row[index], gini, groups
return {'index':b_index, 'value':b_value, 'groups':b_groups}
# Create a terminal node value
def to_terminal(group):
outcomes = [row[-1] for row in group]
return max(set(outcomes), key=outcomes.count)
# Create child splits for a node or make terminal
def split(node, max_depth, min_size, depth):
left, right = node['groups']
del(node['groups'])
# check for a no split
if not left or not right:
node['left'] = node['right'] = to_terminal(left + right)
return
# check for max depth
if depth >= max_depth:
node['left'], node['right'] = to_terminal(left), to_terminal(right)
return
# process left child
if len(left) <= min_size:
node['left'] = to_terminal(left)
else:
node['left'] = get_split(left)
split(node['left'], max_depth, min_size, depth+1)
# process right child
if len(right) <= min_size:
node['right'] = to_terminal(right)
else:
node['right'] = get_split(right)
split(node['right'], max_depth, min_size, depth+1)
# Build a decision tree
def build_tree(train, max_depth, min_size):
root = get_split(dataset)
split(root, max_depth, min_size, 1)
return root
# Print a decision tree
def print_tree(node, depth=0):
if isinstance(node, dict):
print('%s[X%d < %.3f]' % ((depth*' ', (node['index']+1), node['value'])))
print_tree(node['left'], depth+1)
print_tree(node['right'], depth+1)
else:
print('%s[%s]' % ((depth*' ', node)))
dataset = [[2.771244718,1.784783929,0],
[1.728571309,1.169761413,0],
[3.678319846,2.81281357,0],
[3.961043357,2.61995032,0],
[2.999208922,2.209014212,0],
[7.497545867,3.162953546,1],
[9.00220326,3.339047188,1],
[7.444542326,0.476683375,1],
[10.12493903,3.234550982,1],
[6.642287351,3.319983761,1]]
tree = build_tree(dataset, 1, 1)
print_tree(tree)
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
- 68.
- 69.
- 70.
- 71.
- 72.
- 73.
- 74.
- 75.
- 76.
- 77.
- 78.
- 79.
- 80.
- 81.
- 82.
- 83.
- 84.
- 85.
- 86.
- 87.
- 88.
- 89.
- 90.
- 91.
在运行过程中,我们能修改树的最大深度,并在打印的树上观察其影响。
当最大深度为 1 时(即调用 build_tree() 函数时第二个参数),我们可以发现该树使用了我们之前发现的完美分割点(作为树的唯一分割点)。该树只有一个节点,也被称为决策树桩。
[X1 < 6.642]
[0]
[1]
- 1.
- 2.
- 3.
当最大深度加到 2 时,我们迫使输算法不需要分割的情况下强行分割。结果是,X1 属性在左右叉上被使用了两次来分割这个本已经完美分割的数据。
[X1 < 6.642]
[X1 < 2.771]
[0]
[0]
[X1 < 7.498]
[1]
[1]
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
最后,我们可以试试最大深度为 3 的情况:
[X1 < 6.642]
[X1 < 2.771]
[0]
[X1 < 2.771]
[0]
[0]
[X1 < 7.498]
[X1 < 7.445]
[1]
[1]
[X1 < 7.498]
[1]
[1]
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
这些测试表明,我们可以优化代码来避免不必要的分割。请参见延伸章节的相关内容。
现在我们已经可以(完整地)创建一棵决策树了,那么我们来看看如何用它来在新数据上做出预测吧。
2.4 利用模型进行预测
使用决策树模型进行决策,需要我们根据给出的数据遍历整棵决策树。
与前面相同,我们仍需要使用一个递归函数来实现该过程。其中,基于某分割点对给出数据的影响,相同的预测规则被应用到左子节点或右子节点上。
我们需要检查对某子节点而言,它是否是一个可以被作为预测结果返回的终端节点,又或是他是否含有下一层的分割节点需要被考虑。
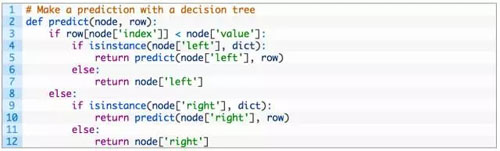
如下是实现上述过程的名为 predict() 函数,你可以看到它是如何处理给定节点的下标与数值的。
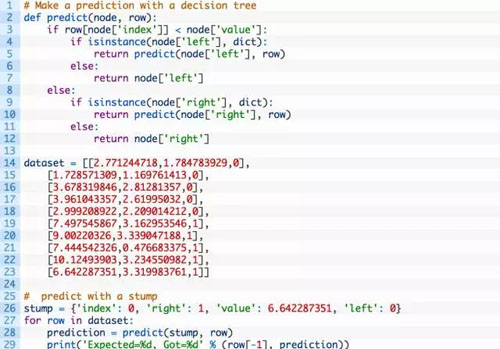
接着,我们使用合成的数据集来测试该函数。如下是一个使用仅有一个节点的硬编码树(即决策树桩)的案例。该案例中对数据集中的每个数据进行了预测。
运行该例子,它将按照预期打印出每个数据的预测结果。
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
现在,我们不仅掌握了如何创建一棵决策树,同时还知道如何用它进行预测。那么,我们就来试试在实际数据集上来应用该算法吧。
2.5 对钞票数据集的案例研究
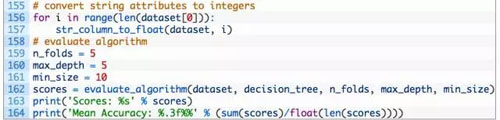
该节描述了在钞票数据集上使用了 CART 算法的流程。
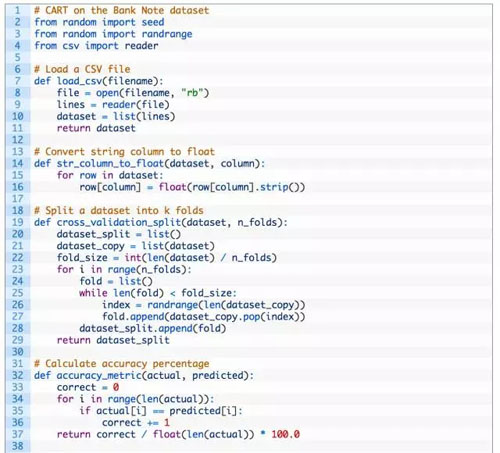
第一步是导入数据,并转换载入的数据到数值形式,使得我们能够用它来计算分割点。对此,我们使用了辅助函数 load_csv() 载入数据及 str_column_to_float() 以转换字符串数据到浮点数。
我们将会使用 5 折交叉验证法(5-fold cross validation)来评估该算法的表现。这也就意味着,对一个记录,将会有 1273/5=274.4 即 270 个数据点。我们将会使用辅助函数 evaluate_algorithm() 来评估算法在交叉验证集上的表现,用 accuracy_metric() 来计算预测的准确率。
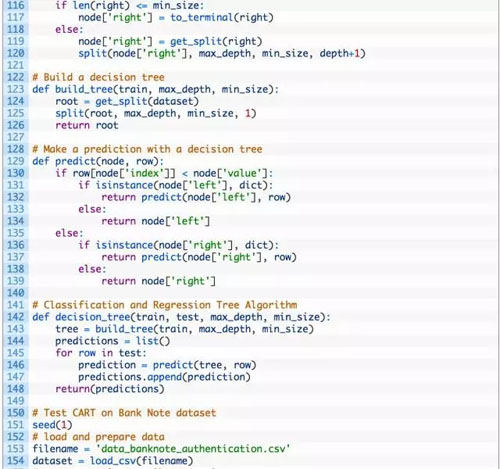
完成的代码如下:
上述使用的参数包括:max_depth 为 5,min_size 为 10。经过了一些实现后,我们确定了上述 CART 算法的使用的参数,但这不代表所使用的参数就是最优的。
运行该案例,它将会 print 出对每一部分数据的平均分类准确度及对所有部分数据的平均表现。
从数据中你可以发现,CART 算法选择的分类设置,达到了大约 83% 的平均分类准确率。其表现远远好于只有约 50% 正确率的零规则算法(Zero Rule algorithm)。
Scores: [83.57664233576642, 84.30656934306569, 85.76642335766424, 81.38686131386861, 81.75182481751825]
Mean Accuracy: 83.358%
三、延伸
本节列出了关于该节的延伸项目,你可以根据此进行探索。
1. 算法调参(Algorithm Tuning):在钞票数据集上使用的 CART 算法未被调参。你可以尝试不同的参数数值以获取更好的更优的结果。
2. 交叉熵(Cross Entropy):另一个用来评估分割点的成本函数是交叉熵函数(对数损失)。你能够尝试使用该成本函数作为替代。
3. 剪枝(Tree Pruning):另一个减少在训练过程中过拟合程度的重要方法是剪枝。你可以研究并尝试实现一些剪枝的方法。
4. 分类数据集(Categorical Dataset):在上述例子中,其树模型被设计用于解决数值型或有序数据。你可以尝试修改树模型(主要修改分割的属性,用等式而非排序的形式),使之能够应对分类型的数据。
5. 回归问题(Regression):可以通过使用不同的成本函数及不同的创建终端节点的方法,来让该模型能够解决一个回归问题。
6. 更多数据集:你可以尝试将该算法用于 UCI Machine Learning Repository 上其他的数据集。
【本文是51CTO专栏机构机器之心的原创文章,微信公众号“机器之心( id: almosthuman2014)”】