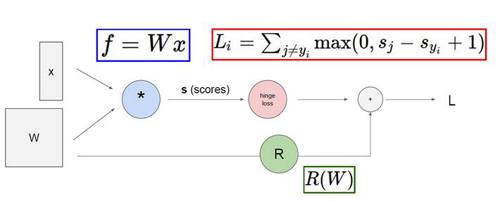
反向传播:
咱们在之前的课程讲了一系列的前向传播的知识点,前向传播也就是从输入到最终计算出LOSS值这一系列过程,那么这节课咱们要讲一个更重要的知识点也就是反向传播。反向传播最直观的意思就是说咱们要从LOSS值入手一步步的往回看,看什么呢?就是要看咱们的每一个权重参数对最终的LOSS值做了多大的贡献。
最简单的小例子
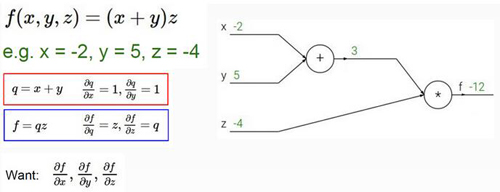
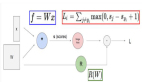
首先咱们用一个最简单的小例子来看一下反向传播是怎么一回事,如上图最终的LOSS值等于-12下面咱们就要算对于X,Y,Z三个输入来说分别对于LOSS值做了多大的贡献,首先咱们用q=x+y,f=qz分别表示中间的计算过程。那么咱们要算什么呢?反向传播最终要算的就是最终的LOSS值对X,Y,Z三个输入的偏导数,这个偏导数该怎么算呢?在这里我们遵循一个链式法则也就是对于输入来说他对于最终LOSS的贡献等于他前面传播下来的梯度再乘以自身的梯度。
链式法则
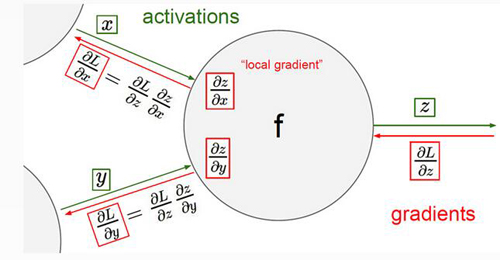
这里就是梯度传播的计算方式,我们要算X和Y对于最终LOSS的贡献(换句话说就是反向传播到X和Y的梯度的大小)要先算前面一层传播到X和Y的梯度再去计算X和Y自身的梯度。
稍难的例子
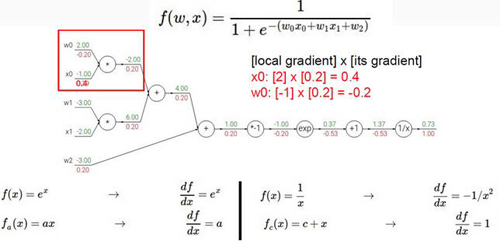
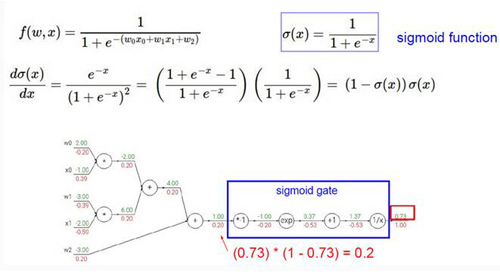
咱们再来看一个稍微难一些的例子,上图表示的是咱们之前说过的这个SIGMOID函数,咱们接下来要算的就是这个函数梯度传播的过程,导数计算的公式我已经写在图上了,咱们只需要根据导数的计算方式一步步的从最终的LOSS值往回算就可以了,下面浅红色的值就是梯度传播的值。
这里我们可以看到梯度传播可以是一步一步的传播也可以一步传播一整块,这一整块我们把它当做是一个整体,相应的就要计算这一整个块的梯度了,也就是直接对SIGMOID函数求导。
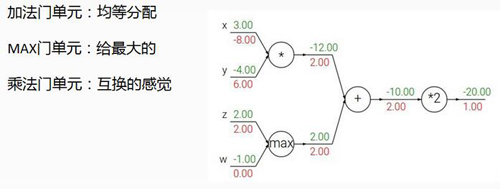
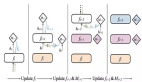
梯度传播的门
这里咱们所说的门就是一个单位区域,我们可以从图中看出来咱们在计算梯度传播的过程中无外乎就是这几种门的操作,每种门也都有它各自的特性,他们的特性是怎么得出的呢?这里就不带大家一步步算了,咱们可以动动笔算一下梯度的传播然后就知道为什么这些门有不同的特性了。
反向传播就先说到这里了,这里只是很简单的谈了一下反向传播具体的计算过程如果同学们还是不太理解建议看一下原始课程会有很详细的推导。
【本文是51CTO专栏作者唐宇迪的原创稿件,转载请注明出处】