我们的数字音频处理技术第三部分涵盖了信号调制内容,将解释如何进行调幅(Amplitude Modulation)、颤音效果(Tremolo Effect)和频率变化(Frequency Variation)。
调制
调幅
正如它的名字暗示的那样, 影响正弦信号的振幅变化依据传递的信息而不断改变。正弦波因为承载着大量的信息被称作载波(carrier)。这种调制技术被用于许多的商业广播和市民信息传输波段(AM)。
为何要使用调幅技术?
调制发射
假设信道是免费资源,有天线就可以发射和接收信号。这要求有效的电磁信号发射天线,它的大小和要被发射的信号的波长应该是同一数量级。很多信号,包括音频成分,通常在 100 赫兹或更低。对于这些信号,如果直接发射,我们就需要建立长达 300 公里的天线。如果通过信号调制将信息加载到 100MHz 的高频载波中,那么天线仅仅需要 1 米(横向长度)。
集中调制与多通道
假设多个信号占用一个通道,调制可以将不同的信号不同频域位置,以便接收者选择该特定信号。使用集中调制(“复用”)的应用有遥感探测数据、立体声调频收音机和长途电话等。
克服设备限制的调制
信号处理设备,比如过滤器、放大器,以及可以用它们简单组成的设备,它们的性能依赖于信号在频域中的境况以及高频率和低频信号的关系。调制可以用于传递信号到频域中的更容易满足设计需求的位置。调制也可以将“宽带信号“(高频和低频的比例很大的信号)转换成”窄带“信号。
音频特效
许多音频特效由于引人注目和处理信号的便捷性使用了调幅技术。我们可以说出很多,比如颤音、合唱、镶边等等。这种实用性就是我们关注它的原因。
颤音效果
颤音效果是调幅最简单的应用,为实现这样的效果,我们会用周期信号改变(乘)音频信号,使用正弦或其他。
- >> tremolo='tremolo.ogg';
- >> fs=44100;
- >> t=0:1/fs:10;
- >> wo=2*pi*440*t;
- >> wa=2*pi*1.2*t;
- >> audiowrite(tremolo, cos(wa).*cos(wo),fs);
Tremolo
这将创造一个正弦形状的信号,它的效果就像‘颤音’。
Tremolo Shape
在真实音频文件中的颤音
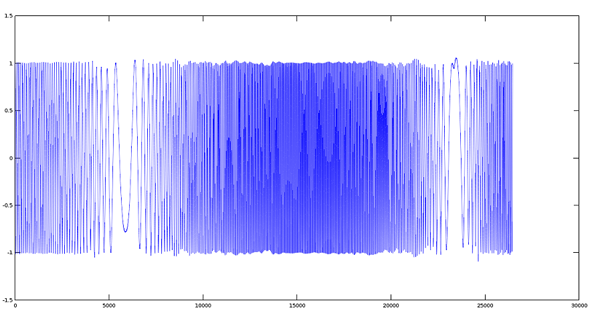
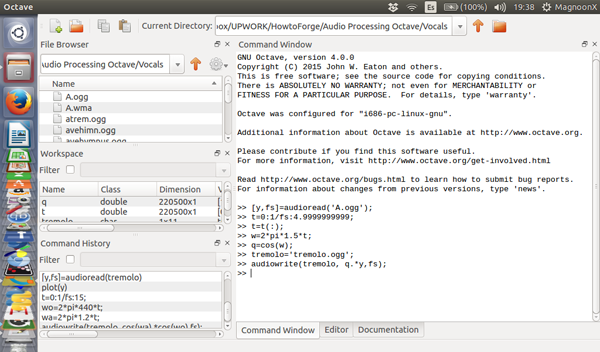
现在我们将展示真实世界中的颤音效果。首先,我们使用之前记录过男性发声 ‘A’ 的音频文件。这个信号图就像下面这样:
- >> [y,fs]=audioread('A.ogg');
- >> plot(y);
Vocal
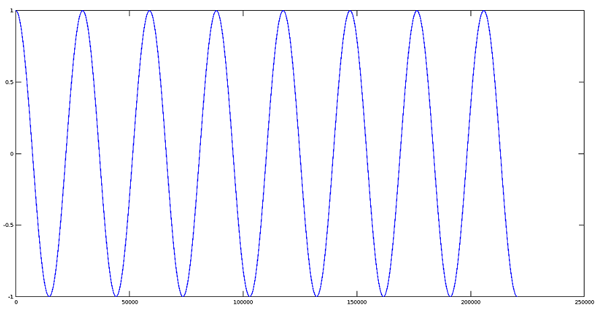
现在我们将创建一个完整的正弦信号,使用如下的参数:
- 增幅 = 1
- 频率= 1.5Hz
- 相位 = 0
- >> t=0:1/fs:4.99999999;
- >> t=t(:);
- >> w=2*pi*1.5*t;
- >> q=cos(w);
- >> plot(q);
注意: 当我们创建一组时间值时,默认情况下,它是以列的格式呈现,如, 1x220500 的值。为了乘以这样的值,必须将其变成行的形式(220500x1)。这就是 t=t(:) 命令的作用。
Sinusodial
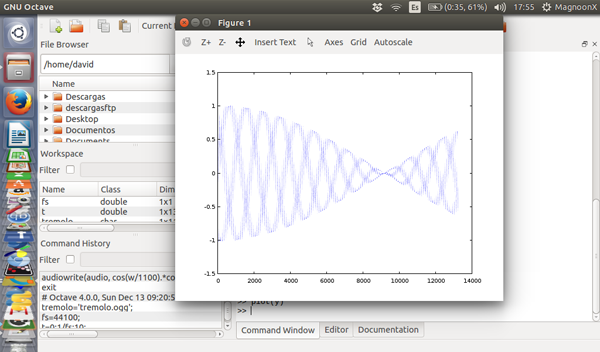
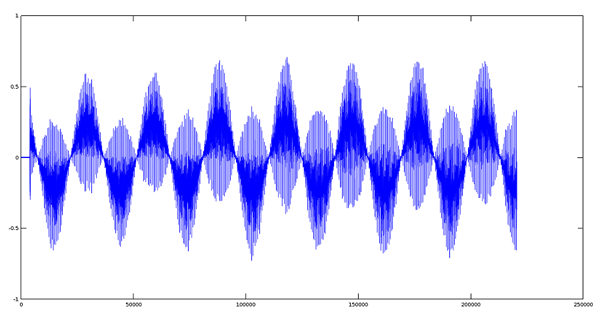
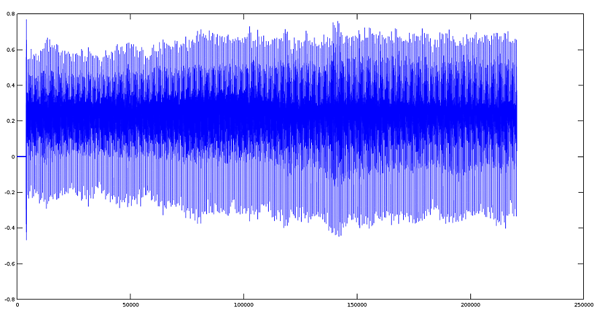
我们将创建第二份 ogg 音频格式的文件,它包含了如下的调制信号:
- >> tremolo='tremolo.ogg';
- >> audiowrite(tremolo, q.*y,fs);
Tremolo Signal
频率变化
我们可以改变频率实现一些有趣的音效,比如原音变形,电影音效,多人比赛。
正弦频率调制的影响
这是正弦调制频率变化的演示代码,根据方程:
- Y=Ac*Cos(wo*Cos(wo/k))
这里:
- Ac = 增幅
- wo = 基频
- k = 标量除数
- >> fm='fm.ogg';
- >> fs=44100;
- >> t=0:1/fs:10;
- >> w=2*pi*442*t;
- >> audiowrite(fm, cos(cos(w/1500).*w), fs);
- >> [y,fs]=audioread('fm.ogg');
- >> figure (); plot (y);
信号图:
你可以使用几乎任何类型的周期函数频率调制。本例中,我们仅仅用了一个正弦函数。请大胆的改变函数频率,用复合函数,甚至改变函数的类型。