毫无疑问机器学习是大数据分析不可或缺的一部分,在使用机器学习技术的时候工程师除了要选择合适的算法之外还需要选择合适的样本数据。那么工程师到底应该选择哪些样本数据、选择多少样本数据才最合适呢?来自于Google的软件工程师Malay Haldar最近发表了一篇题为《数据模型需要多少训练数据》的文章对此进行了介绍。
训练数据的质量和数量通常是决定一个模型性能的最关键因素。一旦训练数据准备好,其他的事情就顺理成章了。但是到底应该准备多少训练数据呢?答案是 这取决于要执行的任务,要满足的性能,所拥有的输入特征、训练数据中的噪音、提取特征中的噪音以及模型的复杂程度等因素。而找出这些变量之间相互关系的方 法就是在不同数据量的训练数据上训练模型并绘制学习曲线。但是这仅仅适合于已经有一定数量的训练数据的情况,如果是最开始的时候,或者说只有很少一点训练 数据的情况,那应该怎么办呢?
与死板地给出所谓精确的“正确”答案相比,更靠谱的方法是通过估算和具体的经验法则。例如本文将要介绍的实证方法:首先自动生成很多逻辑回归问题。 然后对生成的每一个问题,研究训练数据的数量与训练模型的性能之间的关系。***通过观察这两者在这一系列问题上的关系总结出一个简单的规则。
生成一系列逻辑回归问题并研究不同数据量的训练数据所造成的影响的代码可以从GitHub上获取。相关代码是基于Tensorflow实现的,运行这些代码不需要任何特殊的软件或者硬件,用户可以在自己的笔记本上运行整个实验。代码运行之后生成的图表如下:
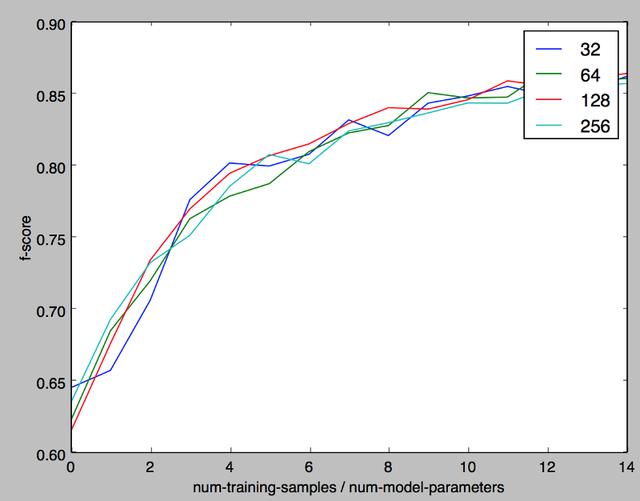
其 中,X轴是训练样本的数量与模型参数数量的比率。Y轴是训练模型的得分(f-score)。不同颜色的曲线表示不同参数数量的模型。例如,红色曲线代表模 型有128个参数,曲线的轨迹表明了随着训练样本从128 x 1到 128 x 2并不断增长的过程中该模型的得分变化。
通过该图表,我们能够发现模型得分并不会随着参数规模的变化而变化。但是这是针对线性模型而言,对于一些隐藏的非线性模型并不适合。当然,更大的模 型需要更多的训练数据,但是对于一个给定的训练模型数量与模型参数数量比率其性能是一样的。该图表还显示,当训练样本的数量与模型参数数量的比率达到 10:1之后,模型得分基本稳定在0.85,该比率便可以作为良好性能模型的一种定义。根据该图表我们可以总结出10X规则,也就是说一个优秀的性能模型 需要训练数据的数量10倍于该模型中参数的数量。
10X规则将估计训练数据数量的问题转换成了需要知道模型参数数量的问题。对于逻辑回归这样的线性模型,参数的数量与输入特征的数量相等,因为模型会为每一个特征分派一个相关的参数。但是这样做可能会有一些问题:
特征可能是稀疏的,因而可能会无法直接计算出特征的数量。
由于正则化和特征选择技术,很多特征可能会被抛弃,因而与原始的特征数相比,真正输入到模型中的特征数会非常少。
避免这些问题的一种方法是:必须认识到估算特征的数量时并不是必须使用标记的数据,通过未标记的样本数据也能够实现目标。例如,对于一个给定的大文 本语料库,可以在标记数据进行训练之前通过生成单词频率的历史图表来理解特征空间,通过历史图表废弃长尾单词进而估计真正的特征数,然后应用10X规则来 估算模型需要的训练数据的数据量。
需要注意的是,神经网络构成的问题集与逻辑回归这样的线性模型并不相同。为了估算神经网络所需要的参数数量,你需要:
如果输入是稀疏的,那么需要计算嵌套层使用的参数的数量。参照word2vec的Tensorflow教程示例。
计算神经网络中边的数量
由于神经网络中参数之间的关系并不是线性的,所以本文基于逻辑回归所做的实证研究并不适合神经网络。但是在这种情况下,可以将10X规则作为训练数据所需数据量的下限。
尽管有上面的问题,根据Malay Haldar的经验,10X规则对于大部分问题还是适用的,包括浅神经网络。如果有疑问,可以在Tensorflow的代码中插入自己的模型和假设,然后运行代码进行验证研究。