在安全领域,“图分析”广泛应用在账户交易异常、不同事件关联等各种场景下。与其他机器学习算法类比较, 其特有的优点在于分析方法符合人的思维方式,分析过程能直观地可视化。
举例来说,下图是把瀚思某客户企业中几类安全事件 : 登陆、使用USB盘、检测到病毒、机器IP、 用户使用机器 - 综合到一起做关联分析。
图中“边”代表发生过事件;点(机器、用户、IP、病毒、USB盘五类之一) 的大小代表事件多少。一张图上我们可以快速定位爆发次数最多的病毒、哪些用户违规使用同台机器、哪些机器使用过同一个USB盘。

下图是另一类例子,瀚思帮银行客户做的交易异常分析:点大小与出度成正比, 颜色随着入度大小按蓝色⇒白色⇒红色方向变化。用金融术语来说:出度过大的叫火山,入度过大的叫黑洞。这类情况往往和诈骗洗钱相关。

但是,图一旦变大,分析过程会变慢,需要分析的边数量,即使最坏不会到全连通有向图中等于节点数N的N*(N-1)/2, 也往往远大于N。而且可视化因为屏幕大小和易读性的限制,不宜再把成千上万个节点和对应的边放到一张图上。
这种情况下,我们采用分而治之策略:利用实际经验中图的社区性特征,把图分割成若干个强联通的区域, 对每一个区域做分析和可视化。
好的图划分算法在实际应用中要额外有三个特征:
1、高速度,***能并行化或者能用GPU加速。
2、能处理小世界网络特征(也就是节点度数呈肥尾分布)。
3、对参数不敏感。
很多算法无法满足2和3,教科书中算法大多是把图均分,而且假设知道图要分为多少类。
根据前文所述,瀚思利用“图计算”在实际应用中,帮助客户解决了有关异常行为检测的工作。而本文将重点针对三类应用广泛、效率较高并可以应用于异常检测的图划分算法进行详述。
谱划分
谱划分算法:它是最早用于解决图划分的一类算法,其思想来源于谱图划分理论。 矩阵的谱就是它的特征值和特征向量。 求图划分准则的***解是一个NP难问题。 一个很好的求解方法是考虑问题的连续松弛形式,将原问题转换成求解Laplacian 矩阵的谱分解, 因此将这类方法统称为谱划分。
假定将每个数据样本看作图中的顶点V,根据样本间的相似度将 顶点间的边 E 赋权重值,便可得到一个基于相似度的无向加权图 G=(V,E). 相似矩阵通常用 W 或 A 表示,有时也称为亲和矩阵(Affinity Matrix), 往往是通过计算高斯核得到。
将相似度矩阵的每行元素相加,即得到对应点的度,以所有度值为对角元素构成的对角矩阵称为度矩阵,通常记为 D。定义好相似矩阵W及度矩阵D,便可得如下的 Laplacian 矩阵:
L=D - W
根据不同的准则函数及谱映射方法,谱划分算法发展了很多不同的具体实现方法,但都可以归纳为下面的三个主要步骤:
对于给定的图G=(V,E),计算图的 Laplacian 矩阵L;
对L矩阵进行特征值分解,取其前 k 个特征值对应的特征向量,构建特征向量矩阵Q;
利用K-means算法或其他经典聚类算法对矩阵Q进行划分,每一行代表一个样本点, 即原图的顶点所属的类别.
上述步骤只是谱划分的一个框架,在具体实现中,还存在着不同的划分准则,常见的有 Minimum Cut,Ratio Cut,Normalized Cut等。
谱划分算法,首先通过引入 Laplacian 矩阵,运用 Laplacian Eigenmap 进行降维,再对这些 低维数据利用聚类算法进行划分,使得运算量大大较少.下图是用谱划分算法实现的效果图:
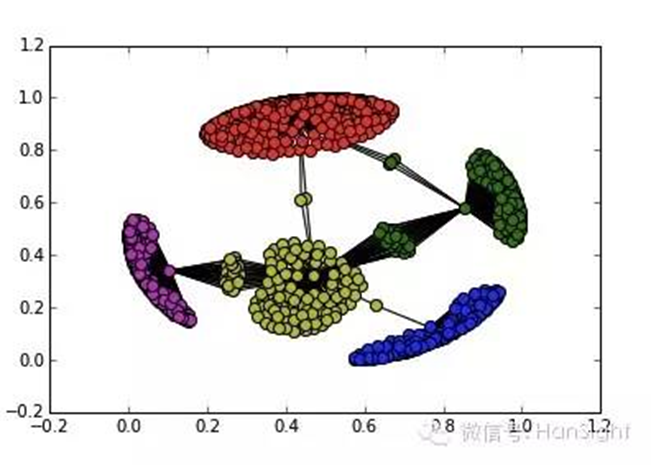
但谱划分算法也有一些不足之处:
1)构建特征向量矩阵Q无疑是该算法中最耗时间的, 在高维情况下, 不说求解特征向量就是求解特征值都非常困难;
2)需要借助先验知识定义递归终止条件,即不具备智能识别图类别总数的能力;
3)现实世界中的复杂网络图往往包含多个类,而递归的二分策略不能保证得到的划分是***的划分。
多层划分算法
第二类图划分算法,称为*多层划分(Multilevel Partitioning,1995,Karypis)*。
以高效及运算时间快著称,比谱划分算法快10%-50%, 计算千万数级的图,时间基本是以秒计算。其主要实现步骤通常分为图的 粗化阶段(Coarsening phase), 初始划分阶段(Initial partitioning phase)和细化阶段 (Uncoarsening phase)三个阶段。
简言之,如下图所示,该算法就是将原始图经粗化阶段一层一层压缩变“小”,得到顶点数目足够小的图, 再将这个数目足够小的图经过初始划分阶段和细化阶段一层一层还原变“大”,直到还原成原始图,完成划分。
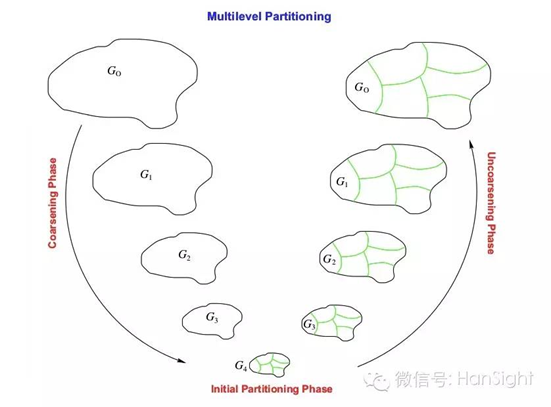
粗化阶段主要是为了减少原始图的复杂性,构建图的多级层次. 它对原始图的点和边进行压缩合并, 构造了一个层次化的较小的图序列, 最终将原始图压缩成一个顶点数目足够小的图。 这种压缩的思想(详见下图)可以形式化地定义为匹配 (Matching),图的匹配是指 边的集合,其中任意两条边都没有公共顶点。 在一个图的所有匹配中,所含匹配边数最多的匹配,称为这个图的***匹配.
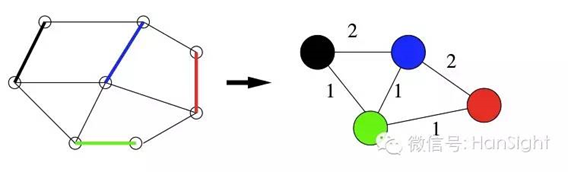
在整个粗化阶段,原始图的所有点以及权重都会累计,最终反应在最小规模图。 将最小规模图进行简单的划分,称为初始划分阶段,该阶段由于结点数目较少,运算非常快,基本不耗时。 也不是多层算法的核心部分,其算法与接下来的细化阶段算法联系比较相似,这里不再赘述.
细化阶段,也可称为图的还原优化阶段,该阶段按照粗化层次一层一层将图还原成原始图,并在还原过程中 利用某些精细的算法逐层优化,直到得到对原始图的划分.
这其中的常见的划分算法有谱二分法算法有Spectral Bisection(SB),Graph Growing Algorithm(GGP), Greedy Refinement(GR), Kernighan-Lin Refinement(KLR)等, 其中比较著名的是Kernighan-Lin划分算法。
*Kernighan-Lin划分算法*,简称KL算法,由Kernighan和Lin在1970年提出,是一个局部搜索优化算法, 优化的目标函数是连接不同类的边权之和最小。
举个简单的例子,如下图,紫色的点属于一类,黑色的点属于一类,KL算法是实现将下图(a)转换成下图(b)的过程。
如何实现将紫色类别中的点和黑色类别中的点进行交换,则是通过计算不同类别损失权重的差值来判断的, 即交换前的内外权重差(如下图(a)的数字所示)减去交换后的内外权重的值。当且仅当该值为正进行交换,否则拒绝交换。 重复以上步骤,直至该值为负。
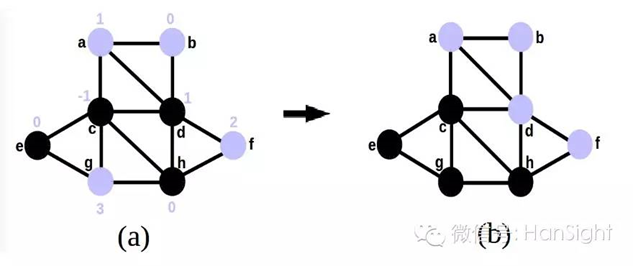
KL算法,较易理解,但得到的解往往是局部***。下图,是利用多层划分算法进行图划分的例子:
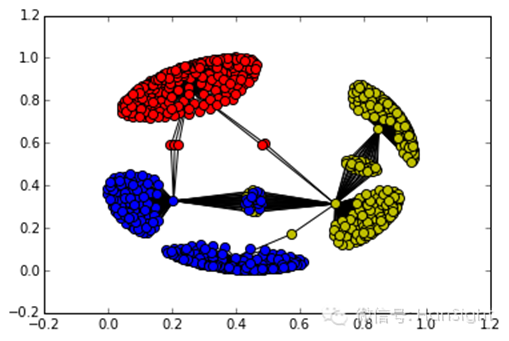
多层划分算法***的局限在于它***的局限性在于需要先验知识来产生一个较好的初始类。
MCL
***谈谈,Markov Cluster Algorithm(2000, Stijn van Dongen), 简称MCL算法,是一种快速可扩展的 无监督图形聚类算法,有时也可以用于图的划分,其思想非常简单,主要是基于 随机游走(Random walk) 和马尔科夫链 (Markov chain)。 先简单说一下这两个概念.
随机游走说的是,如果我们从图中的某一个点开始“瞎转”,那么很可能就会在某一个子图里面转悠,而不是在子图间来回游荡. 而随机游走的计算是通过 Markov链来实现的. Markov链指的是一个随机序列,该序列满足“无后效性”,即 将来的状态只依赖当前状态,而与过去的状态无关。
MCL算法的关键思想就是:”随机漫游者抵达稠密的类后,不会轻易的离开该类”. 前者是随机游走的过程,后者依据是 Markov链的“无后效性”。 MCL算法中随机漫游的过程,其实是一个不断修改转移概率矩阵的过程,该过程 重复执行扩展(Expansion)和膨胀(Inflation)两个操作。
扩展就是前面提到的马尔科夫链的转移矩阵的极限分布, 这个步骤不断地对转移概率矩阵进行自乘直到它不再改变为止。 目的是连接图的不同区域。膨胀是对每一个元素进行幂操作,再将每一列归一化,目的是为了强邻居的连接更强, 弱邻居的连接更弱,也就是让转移矩阵中概率大的概率更大,而小的更小。 这两个操作重复执行一直到概率转移矩阵收敛为止,得到最终的矩阵,根据最终的矩阵便可得结果。
MCL算法对无权图及有权图均试用,划分的子图个数无需事先设定,这是该算法的 ***优势; 划分的子图是非均匀的,试用于长尾分布的数据。 下图就是利用 MCL 进行图划分的结果:
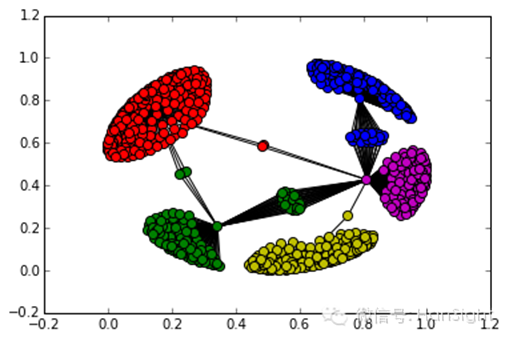
但是MCL算法对图的直径较大的情况不适用. (直径是指两个点之间的距离***值,距离是两个点之间的所有路的长度的最小值)