一、概述
蒙特卡罗方法是一种计算方法。原理是通过大量随机样本,去了解一个系统,进而得到所要计算的值。
它非常强大和灵活,又相当简单易懂,很容易实现。对于许多问题来说,它往往是最简单的计算方法,有时甚至是唯一可行的方法。
它诞生于上个世纪 40 年代美国的”曼哈顿计划”,名字来源于赌城蒙特卡罗,象征概率。
二、π的计算
***个例子是,如何用蒙特卡罗方法计算圆周率π。
正方形内部有一个相切的圆,它们的面积之比是π/4。
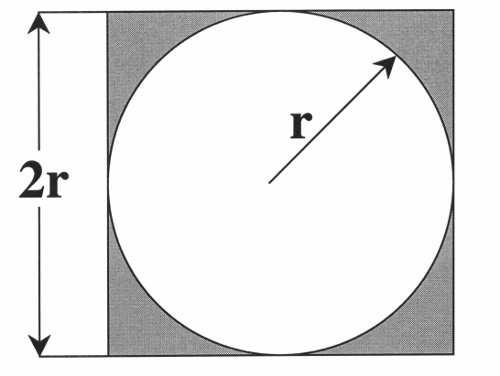
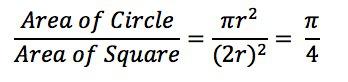
现在,在这个正方形内部,随机产生 10000 个点(即 10000 个坐标对 (x, y)),计算它们与中心点的距离,从而判断是否落在圆的内部。

如果这些点均匀分布,那么圆内的点应该占到所有点的 π/4,因此将这个比值乘以4,就是π的值。通过R语言脚本随机模拟 30000 个点,π的估算值与真实值相差 0.07%。
三、积分的计算
上面的方法加以推广,就可以计算任意一个积分的值。
比如,计算函数 y = x2 在 [0, 1] 区间的积分,就是求出下图红色部分的面积。
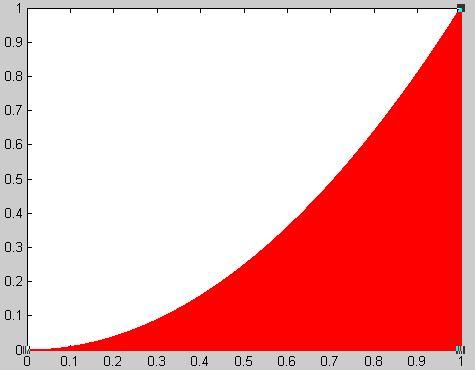
这个函数在 (1,1) 点的取值为1,所以整个红色区域在一个面积为 1 的正方形里面。在该正方形内部,产生大量随机点,可以计算出有多少点落在红色区域(判断条件 y < x2)。这个比重就是所要求的积分值。
用 Matlab 模拟 100 万个随机点,结果为 0.3328。
四、交通堵塞
蒙特卡罗方法不仅可以用于计算,还可以用于模拟系统内部的随机运动。下面的例子模拟单车道的交通堵塞。
根据 Nagel-Schreckenberg 模型,车辆的运动满足以下规则。
- 当前速度是 v 。
- 如果前面没车,它在下一秒的速度会提高到 v + 1 ,直到达到规定的***限速。
- 如果前面有车,距离为d,且 d < v,那么它在下一秒的速度会降低到 d – 1 。
- 此外,司机还会以概率 p 随机减速, 将下一秒的速度降低到 v – 1 。
在一条直线上,随机产生 100 个点,代表道路上的 100 辆车,另取概率 p 为 0.3 。

上图中,横轴代表距离(从左到右),纵轴代表时间(从上到下),因此每一行就表示下一秒的道路情况。
可以看到,该模型会随机产生交通拥堵(图形上黑色聚集的部分)。这就证明了,单车道即使没有任何原因,也会产生交通堵塞。
五、产品厚度
某产品由八个零件堆叠组成。也就是说,这八个零件的厚度总和,等于该产品的厚度。
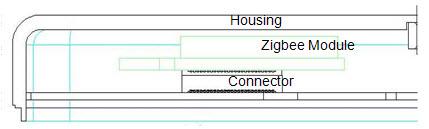
已知该产品的厚度,必须控制在 27mm 以内,但是每个零件有一定的概率,厚度会超出误差。请问有多大的概率,产品的厚度会超出 27mm?
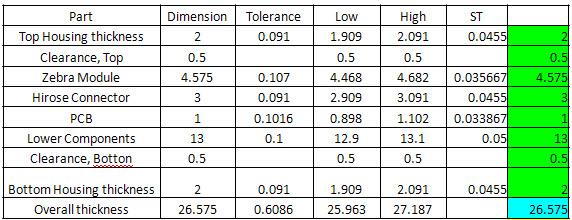
取 100000 个随机样本,每个样本有 8 个值,对应 8 个零件各自的厚度。计算发现,产品的合格率为 99.9979%,即百万分之 21 的概率,厚度会超出 27mm。
六、证券市场
证券市场有时交易活跃,有时交易冷清。下面是你对市场的预测。
- 如果交易冷清,你会以平均价 11 元,卖出 5 万股。
- 如果交易活跃,你会以平均价 8 元,卖出 10 万股。
- 如果交易温和,你会以平均价 10 元,卖出 7.5 万股。
已知你的成本在每股 5.5 元到 7.5 元之间,平均是 6.5 元。请问接下来的交易,你的净利润会是多少?
取 1000 个随机样本,每个样本有两个数值:一个是证券的成本(5.5 元到 7.5 元之间的均匀分布),另一个是当前市场状态(冷清、活跃、温和,各有三分之一可能)。
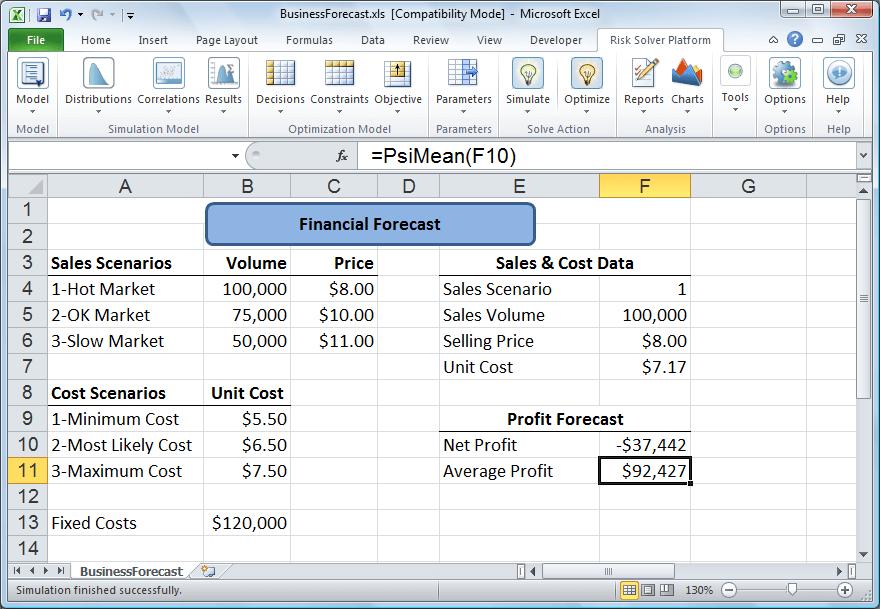
模拟计算得到,平均净利润为 92, 427 美元。