闲不多说。接下来,咱们立刻进入本文章的主题,排序算法。
众所周知,快速排序算法是排序算法中的重头戏。
因此,本文就从快速排序开始。
------------------------------------------------------
一、快速排序算法的基本特性
时间复杂度:O(n*lgn)
最坏:O(n^2)
空间复杂度:O(n*lgn)
不稳定。
快速排序是一种排序算法,对包含n个数的输入数组,平均时间为O(nlgn),最坏情况是O(n^2)。
通常是用于排序的***选择。因为,基于比较的排序,最快也只能达到O(nlgn)。
二、快速排序算法的描述
算法导论,第7章
快速排序时基于分治模式处理的,
对一个典型子数组A[p...r]排序的分治过程为三个步骤:
1.分解:
A[p..r]被划分为俩个(可能空)的子数组A[p ..q-1]和A[q+1 ..r],使得
A[p ..q-1] <= A[q] <= A[q+1 ..r]
2.解决:通过递归调用快速排序,对子数组A[p ..q-1]和A[q+1 ..r]排序。
3.合并。
三、快速排序算法
版本一:
QUICKSORT(A, p, r)
- if p < r
- then q ← PARTITION(A, p, r) //关键
- QUICKSORT(A, p, q - 1)
- QUICKSORT(A, q + 1, r)
数组划分
快速排序算法的关键是PARTITION过程,它对A[p..r]进行就地重排:
- PARTITION(A, p, r)
- x ← A[r]
- i ← p - 1
- for j ← p to r - 1
- do if A[j] ≤ x
- then i ← i + 1
- exchange A[i] <-> A[j]
- exchange A[i + 1] <-> A[r]
- return i + 1
ok,咱们来举一个具体而完整的例子。
来对以下数组,进行快速排序,
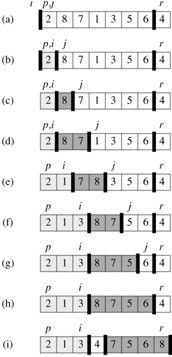
2 8 7 1 3 5 6 4(主元)
一、
i p/j
2 8 7 1 3 5 6 4(主元)
j指的2<=4,于是i++,i也指到2,2和2互换,原数组不变。
j后移,直到指向1..
二、
j(指向1)<=4,于是i++
i指向了8,所以8与1交换。
数组变成了:
i j
2 1 7 8 3 5 6 4
三、j后移,指向了3,3<=4,于是i++
i这是指向了7,于是7与3交换。
数组变成了:
i j
2 1 3 8 7 5 6 4
四、j继续后移,发现没有再比4小的数,所以,执行到了***一步,
即上述PARTITION(A, p, r)代码部分的 第7行。
因此,i后移一个单位,指向了8
i j
2 1 3 8 7 5 6 4
A[i + 1] <-> A[r],即8与4交换,所以,数组最终变成了如下形式,
2 1 3 4 7 5 6 8
ok,快速排序***趟完成。
4把整个数组分成了俩部分,2 1 3,7 5 6 8,再递归对这俩部分分别快速排序。
i p/j
2 1 3(主元)
2与2互换,不变,然后又是1与1互换,还是不变,***,3与3互换,不变,
最终,3把2 1 3,分成了俩部分,2 1,和3.
再对2 1,递归排序,最终结果成为了1 2 3.
7 5 6 8(主元),7、5、6、都比8小,所以***趟,还是7 5 6 8,
不过,此刻8把7 5 6 8,分成了 7 5 6,和8.[7 5 6->5 7 6->5 6 7]
再对7 5 6,递归排序,最终结果变成5 6 7 8。
ok,所有过程,全部分析完成。
***,看下我画的图:
快速排序算法版本二
不过,这个版本不再选取(如上***版本的)数组的***一个元素为主元,
而是选择,数组中的***个元素为主元。
- /**************************************************/
- /* 函数功能:快速排序算法 */
- /* 函数参数:结构类型table的指针变量tab */
- /* 整型变量left和right左右边界的下标 */
- /* 函数返回值:空 */
- /* 文件名:quicsort.c 函数名:quicksort () */
- /**************************************************/
- void quicksort(table *tab,int left,int right)
- {
- int i,j;
- if(left<right)
- {
- i=left;j=right;
- tab->r[0]=tab->r[i]; //准备以本次最左边的元素值为标准进行划分,先保存其值
- do
- {
- while(tab->r[j].key>tab->r[0].key&&i<j)
- j--; //从右向左找第1个小于标准值的位置j
- if(i<j) //找到了,位置为j
- {
- tab->r[i].key=tab->r[j].key;i++;
- } //将第j个元素置于左端并重置i
- while(tab->r[i].key<tab->r[0].key&&i<j)
- i++; //从左向右找第1个大于标准值的位置i
- if(i<j) //找到了,位置为i
- {
- tab->r[j].key=tab->r[i].key;j--;
- } //将第i个元素置于右端并重置j
- }while(i!=j);
- tab->r[i]=tab->r[0]; //将标准值放入它的最终位置,本次划分结束
- quicksort(tab,left,i-1); //对标准值左半部递归调用本函数
- quicksort(tab,i+1,right); //对标准值右半部递归调用本函数
- }
- }
----------------
ok,咱们,还是以上述相同的数组,应用此快排算法的版本二,来演示此排序过程:
这次,以数组中的***个元素2为主元。
2(主) 8 7 1 3 5 6 4
请细看:
2 8 7 1 3 5 6 4
i-> <-j
(找大) (找小)
一、j
j找***个小于2的元素1,1赋给(覆盖重置)i所指元素2
得到:
1 8 7 3 5 6 4
i j
二、i
i找到***个大于2的元素8,8赋给(覆盖重置)j所指元素(NULL<-8)
1 7 8 3 5 6 4
i <-j
三、j
j继续左移,在与i碰头之前,没有找到比2小的元素,结束。
***,主元2补上。
***趟快排结束之后,数组变成:
1 2 7 8 3 5 6 4
第二趟,
7 8 3 5 6 4
i-> <-j
(找大) (找小)
一、j
j找到4,比主元7小,4赋给7所处位置
得到:
4 8 3 5 6
i-> j
二、i
i找比7大的***个元素8,8覆盖j所指元素(NULL)
4 3 5 6 8
i j
4 6 3 5 8
i-> j
i与j碰头,结束。
第三趟:
4 6 3 5 7 8
......
以下,分析原理,一致,略过。
***的结果,如下图所示:
1 2 3 4 5 6 7 8
相信,经过以上内容的具体分析,你一定明了了。
***,贴一下我画的关于这个排序过程的图:
完。一月五日补充。
OK,上述俩种算法,明白一种即可。
-------------------------------------------------------------
五、快速排序的最坏情况和最快情况。
最坏情况发生在划分过程产生的俩个区域分别包含n-1个元素和一个0元素的时候,
即假设算法每一次递归调用过程中都出现了,这种划分不对称。那么划分的代价为O(n),
因为对一个大小为0的数组递归调用后,返回T(0)=O(1)。
估算法的运行时间可以递归的表示为:
T(n)=T(n-1)+T(0)+O(n)=T(n-1)+O(n).
可以证明为T(n)=O(n^2)。
因此,如果在算法的每一层递归上,划分都是***程度不对称的,那么算法的运行时间就是O(n^2)。
亦即,快速排序算法的最坏情况并不比插入排序的更好。
此外,当数组完全排好序之后,快速排序的运行时间为O(n^2)。
而在同样情况下,插入排序的运行时间为O(n)。
//注,请注意理解这句话。我们说一个排序的时间复杂度,是仅仅针对一个元素的。
//意思是,把一个元素进行插入排序,即把它插入到有序的序列里,花的时间为n。
再来证明,最快情况下,即PARTITION可能做的最平衡的划分中,得到的每个子问题都不能大于n/2.
因为其中一个子问题的大小为|_n/2_|。另一个子问题的大小为|-n/2-|-1.
在这种情况下,快速排序的速度要快得多。为,
T(n)<=2T(n/2)+O(n).可以证得,T(n)=O(nlgn)。
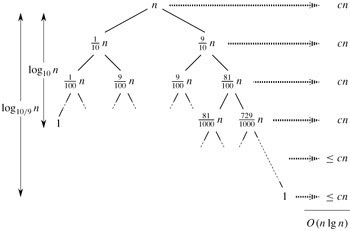
直观上,看,快速排序就是一颗递归数,其中,PARTITION总是产生9:1的划分,
总的运行时间为O(nlgn)。各结点中示出了子问题的规模。每一层的代价在右边显示。
每一层包含一个常数c。
=============================================
请各位自行,思考以下这个版本,对应于上文哪个版本?
- HOARE-PARTITION(A, p, r)
- x ← A[p]
- i ← p - 1
- j ← r + 1
- while TRUE
- do repeat j ← j - 1
- until A[j] ≤ x
- repeat i ← i + 1
- until A[i] ≥ x
- if i < j
- then exchange A[i] ↔ A[j]
- else return j
我常常思考,为什么有的人当时明明读懂明白了一个算法,
而一段时间过后,它又对此算法完全陌生而不了解了列?
我想,究其根本,还是没有彻底明白此快速排序算法的原理,与来龙去脉...
那作何改进列,只能找发明那个算法的原作者了,从原作者身上,再多挖掘点有用的东西出来。
=========================================
***,再给出一个快速排序算法的简洁示例:
Quicksort函数
- void quicksort(int l, int u)
- { int i, m;
- if (l >= u) return;
- swap(l, randint(l, u));
- m = l;
- for (i = l+1; i <= u; i++)
- if (x[i] < x[l])
- swap(++m, i);
- swap(l, m);
- quicksort(l, m-1);
- quicksort(m+1, u);
- }
如果函数的调用形式是quicksort(0, n-1),那么这段代码将对一个全局数组x[n]进行排序。
函数的两个参数分别是将要进行排序的子数组的下标:l是较低的下标,而u是较高的下标。
函数调用swap(i,j)将会交换x[i]与x[j]这两个元素。
***次交换操作将会按照均匀分布的方式在l和u之间随机地选择一个划分元素。