前言
之前,曾在本BLOG内写过一篇文章,快速排序算法普及教程,不少网友反映此文好懂。然,后来有网友algorithm__,指出,“快速排序算法怎么一步一步想到的列?就如一个P与NP问题。知道了解,证明不难。可不知道解之前,要一点一点、一步一步推导出来,好难阿?”
其实,这个问题,我也想过很多次了。之前,也曾在博客里多次提到过。那么,到底为什么,有不少人看了我写的快速排序算法,过了一段时间后,又不清楚快排是怎么一回事了列?
“很大一部分原因,就是只知其表,不知其里,只知其用,不知其本质。很多东西,都是可以从本质看本质的。而大部分人没有做到这一点。从而看了又忘,忘了再看,如此,在对知识的一次一次重复记忆中,始终未能透析本质,从而,形成不好的循环。
所以,归根究底,学一个东西,不但要运用自如,还要通晓其原理,来龙去脉与本质。正如侯捷先生所言,只知一个东西的用法,却不知其原理,实在不算高明。你提出的问题,非常好。我会再写一篇文章,彻底阐述快速排序算法是如何设计的,以及怎么一步一步来的。”
ok,那么现在,我就来彻底分析下此快速排序算法,希望能让读者真正理解此算法,通晓其来龙去脉,明白其内部原理。本文着重分析快速排序算法的过程来源及其时间复杂度。
一、快速排序最初的版本
快速排序的算法思想(此时,还不叫做快速排序)最初是由,一个名叫C.A.R.Hoare提出的,他给出的算法思想描述的具体版本,如下:
HOARE-PARTITION(A, p, r)
- x ← A[p]
- i ← p - 1
- j ← r + 1
- while TRUE
- do repeat j ← j - 1
- until A[j] ≤ x
- repeat i ← i + 1
- until A[i] ≥ x
- if i < j
- then exchange A[i] ↔ A[j]
- else return j
后来,此版本又有不少的类似变种。下面,会具体分析。
二、Hoare版本的具体分析
Hoare在算法导论第7章***的思考题7-1有所阐述。
在上面,我们已经知道,Hoare的快速排序版本可以通过前后俩个指针,分别指向首尾,分别比较而进行排序。
下面,分析一下此版本:
I、 俩个指针,i指向序列的首部,j指着尾部,即i=1,j=n,取数组中***个元素ki为主元,即key<-ki(赋值)。
II、赋值操作(注,以下“->”,表示的是赋值):
j(找小),从右至左,不断--,直到遇到***个比key小的元素kj,ki<-kj。
i(找大),从左至右,不断++,直到遇到***个比key大的元素ki,kj<-ki。
III、按上述方式不断进行,直到i,j碰头,ki=key,***趟排序完成接下来重复II步骤,递归进行。
当过程HOARE-PARTITION结束后,A[p..j](此处在算法导论中文版第二版中出现了印刷错误,被印成了A[p..r])中的每个元素都小于或等于A[j+1..r]每一个元素。HOARE-PARTITION与下文将要介绍的标准PARTITION划分方法不同,HOARE-PARTITION总是将主元值放入两个划分A[p..j]和A[j+1..r]中的某一个之中。因为p<<j<<r,故这种划分总是会结束的。
接下来,咱们来看下上述HOARE-PARTITION划分方法在数组A=[13,19,9,5,12,8,7,4,11,2,6,21]上的运行过程,如下:
i(找大) (找小)j
13 19 9 5 12 8 7 4 11 2 6 21
i j
13 19 9 5 12 8 7 4 11 2 6 21
i j
6 19 9 5 12 8 7 4 11 2 13 21
j i
6 2 9 5 12 8 7 4 11 19 13 21
i j
6 2 9 5 12 8 7 4 11 19 13 21
i j
4 2 9 5 12 8 7 6 11 19 13 21
ij
4 2 5 9 12 8 7 6 11 19 13 21
.....
2 4 5 6 7 8 9 11 12 13 19 21
三、Hoare变种版本
I、取俩个指针i,j,开始时,i=2,j=n,且我们确定,最终完成排序时,左边子序列的数<=右边子序列。
II、矫正位置,不断交换
i-->(i从左至右,右移,找比***个元素要大的)
通过比较ki与k1,如果Ri在分划之后最终要成为左边子序列的一部分,
则i++,且不断i++,直到遇到一个该属于右边子序列Ri(较大)为止。
<--j(j从右至左,左移,找比***个元素要小的)
类似的,j--,直到遇到一个该属于左边子序列的较小元素Rj(较小)为止,
如此,当i<j时,交换Ri与Rj,即摆正位置麻,把较小的放左边,较大的放右边。
III、然后以同样的方式处理划分的记录,直到i与j碰头为止。这样,不断的通过交换Ri,Rj摆正位置,最终完成整个序列的排序。
举个例子,如下(2为主元):
i-> <-j(找小)
2 8 7 1 3 5 6 4
j所指元素4,大于2,所以,j--,
i <--j
2 8 7 1 3 5 6 4
此过程中,若j 没有遇到比2小的元素,则j 不断--,直到j 指向了1,
i j
2 8 7 1 3 5 6 4
此刻,8与1互换,
i j
2 1 7 8 3 5 6 4
此刻,i 所指元素1,小于2,所以i不动,,j 继续--,始终没有遇到再比2小的元素,最终停至7。
i j
2 1 7 8 3 5 6 4
***,i 所指元素1,与数列中***个元素k1,即2交换,
i
[1] 2 [7 8 3 5 6 4]
这样,2就把整个序列,排成了2个部分,接下来,再对剩余待排序的数递归进行第二趟、第三趟排序....。
由以上的过程,还是可以大致看出此算法的拙陋之处的。如一,在上述***步过程中,j没有找到比2小的元素时,需不断的前移,j--。二,当i所指元素交换 后,无法确保此刻i所指的元素就一定小于2,即i指针,还有可能继续停留在原处,不能移动。如此停留,势必应该会耗费不少时间。
后来,进一步,sedgewick因其排序速率较快,便称之为"快速排序",快速排序也因此而诞生了。并最终一举成名,成为了二十世纪最伟大的10大算法之一。
OK,接下来,咱们来看Hoare的变种版本算法。如下,对序列3 8 7 1 2 5 6 4,进行排序:
1、j--,直到遇到了序列中***个比key值3小的元素2,把2赋给ki,j 此刻指向了空元素。
i j
3 8 7 1 2 5 6 4
i j
=> 2 8 7 1 5 6 4
2、i++,指向8,把8重置给j 所指元素空白处,i 所指元素又为空:
i j
2 8 7 1 5 6 4
i j
=> 2 7 1 8 5 6 4
3、j继续--,遇到了1,还是比3(事先保存的key值)小,1赋给i所指空白处:
i j
2 7 1 8 5 6 4
=> 2 1 7 8 5 6 4
4、同理,i 又继续++,遇到了7,比key大,7赋给j所指空白处,此后,i,j碰头。***趟结束:
i j
2 1 7 8 5 6 4
i j
=> 2 1 7 8 5 6 4
5、***,事先保存的key,即3赋给ki,即i所指空白处,得:
[2 1] 3 [7 8 5 6 4]
所以,整趟下来,便是这样:
3 8 7 1 2 5 6 4
2 8 7 1 3 5 6 4
2 3 7 1 8 5 6 4
2 1 7 3 8 5 6 4
2 1 3 7 8 5 6 4
2 1 3 7 8 5 6 4
后续补充:
如果待排序的序列是逆序数列列?ok,为了说明的在清楚点,再举个例子,对序列 9 8 7 6 5 4 3 2 1排序:
9 8 7 6 5 4 3 2 1 //9为主元
1 8 7 6 5 4 3 2 //j从右向左找小,找到1,赋给***个
1 8 7 6 5 4 3 2 //i从左向右找大,没有找到,直到与j碰头
1 8 7 6 5 4 3 2 9 //***,填上9.
如上,当数组已经是逆序排列好的话,我们很容易就能知道,此时数组排序需要O(N^2)的时间复杂度。稍后下文,会具体分析快速排序的时间复杂度。
***,写程序实现此算法,如下,相信,不用我过多解释了:
- int partition(int data[],int lo,int hi) //引自whatever。
- {
- int key=data[lo];
- int l=lo;
- int h=hi;
- while(l<h)
- {
- while(key<=data[h] && l<h) h--; //高位找小,找到了,就把它弄到前面去
- data[l]=data[h];
- while(data[l]<=key && l<h) l++; //低位找大,找到了,就把它弄到后面去
- data[h]=data[l];
- } //如此,小的在前,大的在后,一分为二
- data[l]=key;
- return l;
- }
后续补充:举个例子,如下(只说明了***趟排序):
3 8 7 1 2 5 6 4
2 8 7 1 5 6 4
2 7 1 8 5 6 4
2 1 7 8 5 6 4
2 1 7 8 5 6 4
2 1 3 7 8 5 6 4 //***补上,关键字3
看到这,不知各位读者,有没有想到我上一篇文章里头的那快速排序的第二个版本?对,上述程序,即那篇文章里头的第二个版本。我把程序揪出来,你一看,就明白了:
- void quicksort(table *tab,int left,int right)
- {
- int i,j;
- if(left<right)
- {
- i=left;j=right;
- tab->r[0]=tab->r[i]; //准备以本次最左边的元素值为标准进行划分,先保存其值
- do
- {
- while(tab->r[j].key>tab->r[0].key&&i<j)
- j--; //从右向左找第1个小于标准值的位置j
- if(i<j) //找到了,位置为j
- {
- tab->r[i].key=tab->r[j].key;i++;
- } //将第j个元素置于左端并重置i
- while(tab->r[i].key<tab->r[0].key&&i<j)
- i++; //从左向右找第1个大于标准值的位置i
- if(i<j) //找到了,位置为i
- {
- tab->r[j].key=tab->r[i].key;j--;
- } //将第i个元素置于右端并重置j
- }while(i!=j);
- tab->r[i]=tab->r[0]; //将标准值放入它的最终位置,本次划分结束
- quicksort(tab,left,i-1); //对标准值左半部递归调用本函数
- quicksort(tab,i+1,right); //对标准值右半部递归调用本函数
- }
- }
我想,至此,已经讲的足够明白了。如果,你还不懂的话,好吧,伸出你的手指,数数吧....ok,再问读者一个问题:像这种i从左至右找大,找到***个比 key大(数组中***个元素置为key),便重置kj,j从右向左找小,找到***个比key小的元素,则重置ki,当然此过程中,i,j都在不断的变化, 通过++,或--,指向着不同的元素。
你是否联想到了,现实生活中,有什么样的情形,与此快速排序算法思想相似?ok,等你想到了,再告诉我,亦不迟。:D。
四、快速排序的优化版本
再到后来,N.Lomuto又提出了一种新的版本,此版本即为快速排序算法中阐述的***个版本,即优化了PARTITION程序,它现在写在了 算法导论 一书上,
快速排序算法的关键是PARTITION过程,它对A[p..r]进行就地重排:
PARTITION(A, p, r)
- x ← A[r] //以***一个元素,A[r]为主元
- i ← p - 1
- for j ← p to r - 1 //注,j从p指向的是r-1,不是r。
- do if A[j] ≤ x
- then i ← i + 1
- exchange A[i] <-> A[j]
- exchange A[i + 1] <-> A[r]
- return i + 1
然后,对整个数组进行递归排序:
- QUICKSORT(A, p, r)
- if p < r
- then q ← PARTITION(A, p, r) //关键
- QUICKSORT(A, p, q - 1)
- QUICKSORT(A, q + 1, r)
举最开头的那个例子:2 8 7 1 3 5 6 4,不过与上不同的是:它不再以***个元素为主元,而是以***一个元素4为主元,且i,j俩指针都从头出发,j 一前,i 一后。i 指元素的前一个位置,j 指着待排序数列中的***个元素。
一、
i p/j-->
2 8 7 1 3 5 6 4(主元)
j 指的2<=4,于是i++,i 也指到2,2和2互换,原数组不变。
j 后移,直到指向1..
二、
j(指向1)<=4,于是i++,i指向了8,
i j
2 8 7 1 3 5 6 4
所以8与1交换,数组变成了:
i j
2 1 7 8 3 5 6 4
三、j 后移,指向了3,3<=4,于是i++
i 这时指向了7,
i j
2 1 7 8 3 5 6 4
于是7与3交换,数组变成了:
i j
2 1 3 8 7 5 6 4
四、j 继续后移,发现没有再比4小的数,所以,执行到了***一步,
即上述PARTITION(A, p, r)代码部分的 第7行。
因此,i后移一个单位,指向了8
i j
2 1 3 8 7 5 6 4
A[i + 1] <-> A[r],即8与4交换,所以,数组最终变成了如下形式,
2 1 3 4 7 5 6 8
ok,快速排序***趟完成。接下来的过程,略。不过,有个问题,你能发现此版本与上述版本的优化之处么?
五、快速排序的深入分析
咱们,再具体分析下上述的优化版本,
- PARTITION(A, p, r)
- x ← A[r]
- i ← p - 1
- for j ← p to r - 1
- do if A[j] ≤ x
- then i ← i + 1
- exchange A[i] <-> A[j]
- exchange A[i + 1] <-> A[r]
- return i + 1
咱们以下数组进行排序,每一步的变化过程是:
i p/j
2 8 7 1 3 5 6 4(主元)
i j
2 1 7 8 3 5 6 4
i j
2 1 3 8 7 5 6 4
i
2 1 3 4 7 5 6 8
由上述过程,可看出,j扫描了整个数组一遍,只要一旦遇到比4小的元素,i 就++,然后,kj、ki交换。那么,为什么当j找到比4小的元素后,i 要++列? 你想麻,如果i始终停在原地不动,与kj 每次交换的ki不就是同一个元素了么?如此,还谈什么排序?。
所以,j在前面开路,i跟在j后,j只要遇到比4小的元素,i 就向前前进一步,然后把j找到的比4小的元素,赋给i,然后,j才再前进。
打个比喻就是,你可以这么认为,i所经过的每一步,都必须是比4小的元素,否则,i就不能继续前行。好比j 是先行者,为i 开路搭桥,把小的元素作为跳板放到i 跟前,为其铺路前行啊。
于此,j扫描到***,也已经完全排查出了比4小的元素,只有***一个主元4,则交给i处理,因为***一步,exchange A[i + 1] <-> A[r]。这样,不但完全确保了只要是比4小的元素,都被交换到了数组的前面,且j之前未处理的比较大的元素则被交换到了后面,而且还是O(N)的时间复杂度,你不得不佩服此算法设计的巧妙。
这样,我就有一个问题了,上述的PARTITION(A, p, r)版本,可不可以改成这样咧?
望读者思考:
- PARTITION(A, p, r) //请读者思考版本。
- x ← A[r]
- i ← p - 1
- for j ← p to r //让j 从p指向了***一个元素r
- do if A[j] ≤ x
- then i ← i + 1
- exchange A[i] <-> A[j]
- exchange A[i + 1] <-> A[r] //去掉此***的步骤
- return i //返回 i,不再返回 i+1.
六、Hoare变种版本与优化后版本的比较
现在,咱们来讨论一个问题,快速排序中,其中对于序列的划分,我们可以看到,已经有以上俩个版本,那么这俩个版本孰优孰劣列?ok,不急,咱们来比较下:
为了看着方便,再贴一下各自的算法,
Hoare变种版本:
HOARE-PARTITION(A, p, r)
- x ← A[p] //以***个元素为主元
- i ← p - 1
- j ← r + 1
- while TRUE
- do repeat j ← j - 1
- until A[j] ≤ x
- repeat i ← i + 1
- until A[i] ≥ x
- if i < j
- then exchange A[i] ↔ A[j]
- else return j
优化后的算法导论上的版本:
- PARTITION(A, p, r)
- x ← A[r] //以***一个元素,A[r]为主元
- i ← p - 1
- for j ← p to r - 1
- do if A[j] ≤ x
- then i ← i + 1
- exchange A[i] <-> A[j]
- exchange A[i + 1] <-> A[r]
- return i + 1
咱们,先举上述说明Hoare版本的这个例子,对序列3 8 7 1 2 5 6 4,进行排序:
Hoare变种版本(以3为主元,红体为主元):
3 8 7 1 2 5 6 4
2 8 7 1 5 6 4 //交换1次,比较4次
2 7 1 8 5 6 4 //交换1次,比较1次
2 1 7 8 5 6 4 //交换1次,比较1次
2 1 7 8 5 6 4 //交换1次,比较0次
2 1 3 7 8 5 6 4 //总计交换4次,比较6次。
//移动了元素3、8、7、1、2.移动范围为:2+3+1+2+4=12.
优化版本(以4为主元):
3 8 7 1 2 5 6 4 //3与3交换,不用移动元素,比较1次
3 1 7 8 2 5 6 4 //交换1次,比较3次
3 1 2 8 7 5 6 4 //交换1次,比较1次
3 1 2 4 7 5 6 8 //交换1次,比较2次。
//即完成,总计交换4次,比较7次。
//移动了元素8、7、1、2、4.移动范围为:6+2+2+2+4=16.
再举一个例子:对序列2 8 7 1 3 5 6 4排序:
Hoare变种版本:
2 8 7 1 3 5 6 4
1 8 7 3 5 6 4 //交换1次,比较5次
1 7 8 3 5 6 4 //交换1次,比较1次
1 2 7 8 3 5 6 4 //交换0次,比较1次。2填上,完成,总计交换2次,比较7次。
优化版本:
2 8 7 1 3 5 6 4 //2与2交换,比较1次
2 1 7 8 3 5 6 4 //交换1次,比较3次
2 1 3 8 7 5 6 4 //交换1次,比较1次
2 1 3 4 7 5 6 8 //交换1次,比较2次。完成,总计交换4次,比较7次。
各位,已经看出来了,这俩个例子说明不了任何问题。到底哪个版本效率更高,还有待进一步验证或者数学证明。ok,等我日后发现更有利的证据再来论证下。
七、快速排序算法的时间复杂度
ok,我想你已经完全理解了此快速排序,那么,我想你应该也能很快的判断出:快速排序算法的平均时间复杂度,即为O(nlgn)。为什么列?因为你 看,j,i扫描一遍数组,花费用时多少?对了,扫描一遍,当然是O(n)了,那样,扫描多少遍列,lgn到n遍,最快lgn,最慢n遍。且可证得,快速排序的平均时间复杂度即为O(n*lgn)。
PARTITION可能做的最平衡的划分中,得到的每个子问题都不能大于n/2.
因为其中一个子问题的大小为|_n/2_|。另一个子问题的大小为|-n/2-|-1.
在这种情况下,快速排序的速度要快得多。为:
T(n)<=2T(n/2)+O(n).可以证得,T(n)=O(nlgn)。
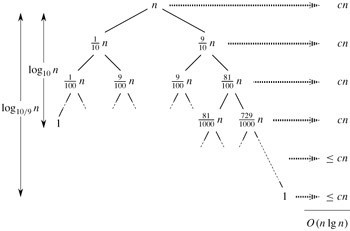
以下给出一个递归树的简单证明:
在分治算法中的三个步骤中, 我们假设分解和合并过程所用的时间分别为D(n), C(n), 设T(n)为处理一个规模为n的序列所消耗的时间为子序列个数,每一个子序列是原序列的1/b,α为把每个问题分解成α个子问题, 则所消耗的时间为:
O(1) 如果n<=c
T(n) =
αT(n/b) + D(n) + C(n)
在快速排序中,α 是为2的, b也为2, 则分解(就是取参照点,可以认为是1), 合并(把数组合并,为n), 因此D(n) + C(n) 是一个线性时间O(n).这样时间就变成了:
T(n) = 2T(n/2) + O(n).
如上图所示,在每个层的时间复杂度为: O(n),一共有Lgn层,每一层上都是cn, 所以共消耗时间为cn*lgn; 则总时间:
cn*lg2n+cn = cn(1+lgn) 即O(nlgn)。
关于T(n)<=2T(n/2)+O(n)=>T(n)=O(nlgn)的严格数学证明,可参考算法导论 第四章 递归式。
而后,我想问读者一个问题,由此快速排序算法的时间复杂度,你想到了什么,是否想到了归并排序的时间复杂度,是否想到了二分查找,是否想到了一课n个结点的红黑树的高度lgn,是否想到了......
八、由快速排序所想到的
上述提到的东西,很早以前就想过了。此刻,我倒是想到了前几天看到的一个荷兰国旗问题。当时,和algorithm__、gnuhpc简单讨论过这个问题。现在,我也来具体解决下此问题:
问题描述:
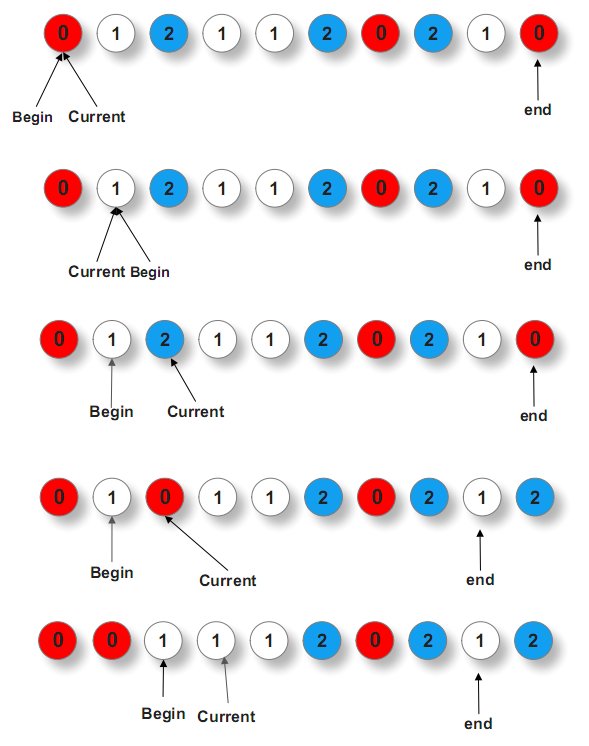
我们将乱序的红白蓝三色小球排列成有序的红白蓝三色的同颜色在一起的小球组。这个问题之所以叫荷兰国旗,是因为我们可以将红白蓝三色小球想象成条状物,有序排列后正好组成荷兰国旗。如下图所示:
这个问题,类似快排中partition过程。不过,要用三个指针,一前begin,一中current,一后end,俩俩交换。
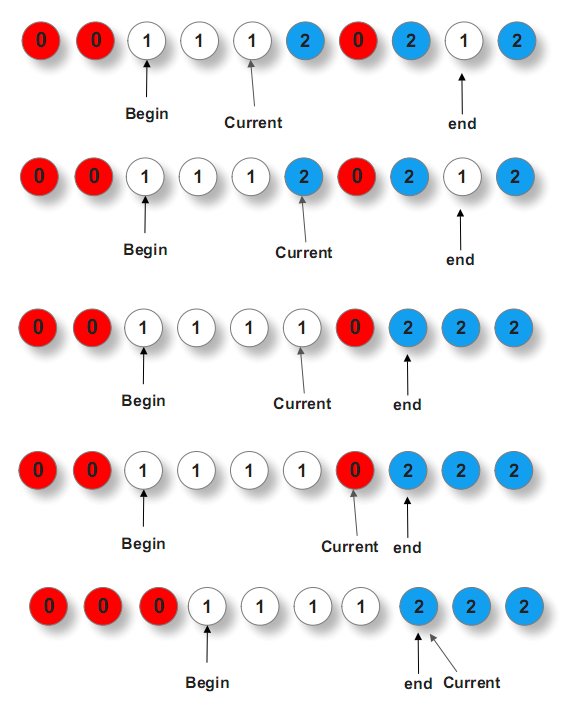
1、current遍历,整个数组序列,current指1不动,
2、current指0,与begin交换,而后current++,begin++,
3、current指2,与end交换,而后,current不动,end--。
为什么,第三步,current指2,与end交换之后,current不动了列,对的,正如algorithm__所说:current之所以与 begin交换后,current++、begin++,是因为此无后顾之忧。而current与end交换后,current不动,end--,是因有 后顾之忧。
为什么啊,因为你想想啊,你最终的目的无非就是为了让0、1、2有序排列,试想,如果第三步,current与end交换之前,万一end之前指的是0, 而current交换之后,current此刻指的是0了,此时,current能动么?不能动啊,指的是0,还得与begin交换列。
ok,说这么多,你可能不甚明了,直接引用下gnuhpc的图,就一目了然了:
本程序主体的代码是:
- //引用自gnuhpc
- while( current<=end )
- {
- if( array[current] ==0 )
- {
- swap(array[current],array[begin]);
- current++;
- begin++;
- }
- else if( array[current] == 1 )
- {
- current++;
- }
- else //When array[current] =2
- {
- swap(array[current],array[end]);
- end--;
- }
- }
看似,此问题与本文关系不大,但是,一来因其余本文中快速排序partition的过程类似,二来因为此问题引发了一段小小的思考,并最终成就了本文。差点忘了,还没回答本文开头提出的问题。所以,快速排序算法是如何想到的,如何一步一步发明的列?答案很简单:多观察,多思考。
ok,测试一下,看看你平时有没有多观察、多思考的习惯:我不知道是否有人真正思考过冒泡排序,如果思考过了,你是否想过,怎样改进冒泡排序列?ok,其它的,我就不多说了,只贴以下这张图:
本文完。
作者:July