浅谈机器学习中的线性回归

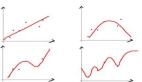
 Cost Function的用途：对假设的函数进行评价，cost function越小的函数，说明拟合训练数据拟合的越好；

    1、最小二乘法：

     何为最小二乘法，其实很简单。我们有很多的给定点，这时候我们需要找出一条线去拟合它，那么我先假设这个线的方程，然后把数据点代入假设的方程得到观测值，求使得实际值与观测值相减的平方和最小的参数。对变量求偏导联立便可求。

      比如测定一个刀具的磨损速度，也就是说，随着使用刀具的次数越多，刀具本身的厚度会逐渐减少，故刀具厚度与使用时间将成线性关系，假设符合f（t）=at + b（t代表时间，f(t)代表刀具本身厚度），a，b是待确定的常数，那么a、b如何确定呢？最理想的情形就是选取这样的a、b，能使直线y = at + b 所得到的值与实际中测量到的刀具厚度完全符合，但实际上这是不可能的，因为误差总是存在难以避免的。故因误差的存在，使得理论值与真实值存在偏差，为使偏差最小通过偏差的平方和最小确定系数a、b，从而确定两变量之间的函数关系f（t）= at + b。这种通过偏差的平方和为最小的条件来确定常数a、b的方法，即为最小二乘法。

    2、线性回归：

    回归在数学上来说是给定一个点集，能够用一条曲线去拟合之，如果这个曲线是一条直线，那就被称为线性回归，如果曲线是一条二次曲线，就被称为二次回归.

    在研究几个变量之间的关联关系，特别当因变量和自变量为线性关系时，它是一种特殊的线性模型。最简单的情形是一个自变量和一个因变量，且它们大体上有线性关系，这叫一元线性回归，即模型为Y=a+bX+ε，这里X是自变量，Y是因变量，ε是随机误差。随机误差一般都是服从均值为0的正态分布。

    所以可以认为线性回归就是给出一系列点用来拟合曲线  h（x）=θ+θ₁X(线性和非线性其实都一个意思，都是寻找合适的参数去满足已有数据的规律。可以通过最小二乘法)，当然多维的时候也是一样的，就是参数多了一点。

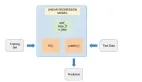
    3、对于线性回归问题的分析流程：

     给出一个函数模型，这个函数模型有很多个未知参数，然后我们代入很多观察数据，但是这样代入后的方程是很难解的，于是我们通过使用求解近似解，转化为求解误差最小化问题。列出误差项后，使用梯度下降或牛顿方法等求解最小值，确定未知参数。

      （1）  给出假设（hypotheses ：h and parameters ：θ）

            [[118565]]

     （2）根据给出的training set，学习求出θ。

           我们给出一个代价函数，其实就是最小二乘法：

          [[118566]]

    （3）找到一个θ使得J(θ)最小。

        我们要求J（Θ），但是我们不知道参数，而且总不能一个一个穷举出来看哪个最小。因此我们用到梯度下降法（gradient descent），找到θ 使得 J（θ）最小。

    4、梯度下降法（gradient descent）

     梯度下降算法是一种求局部***解的方法，对于F(x)，在a点的梯度是F(x)增长最快的方向，那么它的相反方向则是该点下降最快的方向，具体参考wikipedia。

     原理：将函数比作一座山，我们站在某个山坡上，往四周看，从哪个方向向下走一小步，能够下降的最快；

     注意：当变量之间大小相差很大时，应该先将他们做处理，使得他们的值在同一个范围，这样比较准确。

    1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。

    2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。

    描述一下梯度减少的过程，对于我们的函数J(θ)求偏导J： 

    Repeat  until convergence：{

     [[118567]]

    下面是更新的过程，也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

     [[118568]] 

    }

   5、局部加权线性回归：

     对于线性回归问题，一般使用最小二乘法还有牛顿法啦。使用最小二乘法只能说是***，但是并不能知道置信度。还有就是有时候使用线性回归可能导致模拟的曲线“欠拟合”，这种情况下

我们就使用局部加权线性回归，可以比较好的模拟曲线。 就是加个权值而已

                                      [[118569]]

重新构造新的代价函数j(x)

                                 [[118570]]。

我们从权值函数的表示就可以看出，离要求x远的点，权值越小，到***基本为0，也就是说，只有要求x周围的点起作用。 求法还是和上面一样的。

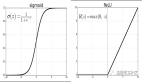
   6、Logistic/Sigmoid Regreesion Mode：

      通过使用一个特定函数，将线性回归问题转化为分类问题，即通过使用这个函数使得y的值在0--1范围之内。这个函数可以是Logistic/Sigmoid这样的。

 其实就是把线性回归的问题拿来做分类，将原来的值域映射到0到1之间。

原文链接：http://www.cnblogs.com/GuoJiaSheng/p/3928160.html