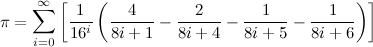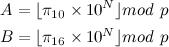查看下文之前,大家可以先想想。来看看 π 值计算世界纪录保持者 Mysticial 的回复。
问题(来自Ishan Sharma):
我曾试过用各种不同的方法,来做一个按序输出显示 π 值的程序。我试过泰勒级数法,但是它收敛地非常慢(这是之后,当我将我的结果和网上的值对比时发现的)。总之,我正试着找出更好的算法。
所以,当我在写这个程序时总遇到问题,不管使用什么算法,我都有一个困惑:我如何才能知道我计算的数字是正确的呢?
最高票数的回答(来自Mysticial):
由于我是计算 π 值的世界纪录保持者(10 万亿位),我来谈一下我的拙见:
除非你是想创造一个新的世界记录,否则通常的解决办法就是对比已知值验证计算值。所以,这很简单。
其实,我就有一个列出了数字片段的网页。它就是为了验证计算值。http://www.numberworld.org/digits/Pi/
但是,当你进入世界记录的范围,就没有已知值让你对比验证了。
通常,验证计算值的标准方法是用另一种算法再计算一次。所以,只要有一个计算错误,数字就不会相同。
这经常会花两倍多的时间(因为第二种算法一般会慢一点)。但这是验证计算值的唯一方法,只要你涉及了从没被计算过的未知领域或是一个新的世界记录,就只能这么做。
在超级计算机保持世界记录的时候,有两种不同的常见AGM算法:
它们都是时间复杂度为 O(N log(N)^2) 的算法,而且相当简单。但是,如今的算法有些不同了。在最近的3个世界记录中,我们只通过最快的公式(Chudnovsky 公式)进行一次运算,而不是两次。
这个算法比较难,但是它比AGM算法快很多。
然后我们用BBP公式进行数字提取,来验证这个二进制数字。
使用这个公式,你可以计算任何二进制数字,并且不用计算它之前的所有数字。因此,它用来验证最后少数的二进制计算值。所以,它比一个完整的计算要快得多。
它的优点是:
1.只需要进行一次复杂的运算。
它的缺点是:
- 需要实现Bailey–Borwein–Plouffe (BBP)公式。
- 需要多一步来验证:基数从二进制到十进制的转换。
我曾列出过一些细节来说明为什么验证最后几个数字就能证明所有数字都是正确的。但这是显而易见的,因为任何计算错误都会传递到最后一个数字。
现在,最后一步(验证转换)实际上是非常重要的。一位前世界纪录保持者曾呼吁我们不要这么做,因为,我一开始并没有给出它详细的过程。
所以,现在我把我博客的这个片段贴出来:
N = #所需的小数位数
p = 64位素数
用10进制算法计算A,用二进制算法算B。
如果 A=B,那么由于“极大可能性”,转换是正确的。
深入阅读,可查看我的这篇博文《Pi – 5 万亿位》。
原文链接: Stack Overflow 翻译: 伯乐在线 - colleen__chen