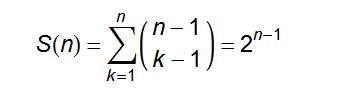对台阶步数问题的数学分析及更优解探索

问题

有这样一个关于台阶和步数的题目：

假设A上台阶，一次可以跨1层，2层，3层.. 或m层，问A上n层台阶，有多少种走法？其中，m和n都是正整数，并且 m <= n

对台阶步数问题提出简单分析，探索是否存在更优解的方案。

 

分析

这个问题等价于：

对于数n，有多少种方案让小于n的数相加等于n，且这些数中的***数不超过m(m<=n) 

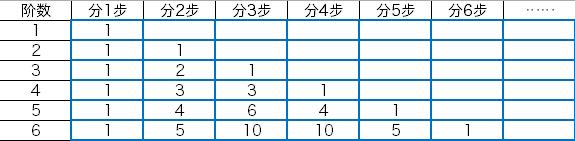
首先考虑m=n时情况

有多少种方案把n拆分成1...n份：

当n=2时，分1种{2}，分2种{1*2}

当n=3时，分1种{3}，分2种[1,2]的排列，分3种{1*3}

当n=4时，分1种{4}，分2种[1,3][2,2]的排列，分3种[1,1,2]的排列，分4种{1*4}

当n=5时，分1种{5}，分2种[1,4][2,3]的排列，分3种[1,1,3][1,2,2]的排列，分4种[1,1,1,2]的排列，分5种{1*5}

当n=6时，分1种{6}，分2种[1,5][2,4][3,3]的排列，分3种[1,1,4][1,2,3][2,2,2]的排列，分4种[1,1,1,3][1,1,2,2]的排列，分5种[1,1,1,1,2]的排列，分6种1*6

……

于是每一步分法都是一个将整数n的进行有序k分拆问题。

根据组合数学定理：正整数n的有序k分拆的个数等于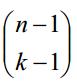。即(n-1)选(k-1)的组合数。

这正是杨辉三角的第n行第k项的通项：

于是，可以得到：

那么 k→1...n 总方案数(即为n从1拆分到n拆分的和的函数，用S(n)记号表示)

   （根据杨辉三角性质）

 

考虑1<m<n的情况：

(非常抱歉因疏于严谨上一版中该部分推测有误，经查证后给出准确方法。特别感谢 @张晋坤 @顾健 等同学的斧正。)

当m<n时，该问题可以描述为，设k施一个给定的正整数，设h_k(n)表示将正整数n拆分分部量只含1,2,3...k的有序分拆数。该问题符合广义斐波那契数定义，则h_k(n)满足：

当n<=k时，h_k(n)=2^n-1

当n>k>=2时，h_k(n)=h_k(n-1)+h_k(n-2)+...+h_k(n-k)

因为n<=k时，正整数n拆成分部量只含1,2..k的有序分拆数，就是n的有序分拆数，而n得有序分拆数就是2^n-1。

所以，根据定理写出了此迭代的循环版本，如下面的wideFib方法。 

总结

以上总结，可以用一分段函数来描述这个问题的通解： 

当m=n时复杂度为O(1)

当m<n时复杂度为O(nm+n)，虽然未能达到线性复杂度，但也能看出具有更小的常数阶。

所以有一定程度的优化改善。

 

示例

利用上面的结论，给出如下代码：

//java  
    
    static long stepsOfTerrace(int n, int m) {  
        if (m > n || n < 2)  
            throw new IllegalArgumentException();  
        if (m == n)  
            return (long) Math.pow(2, n - 1);  
        else if (m > 1)  
            return wideFib(n , m);  
        else 
            return n;  
    }  
 
    static long wideFib(int n, int k) {  
        long[] steps = new long[n];  
        for (int i = 1; i <= n - 1; i++) {  
            if (i <= k)    // hk(k)之前序列=2^n-1  
                steps[i] = (int) Math.pow(2, i - 1);  
            else    // 之后按照广义斐波那契计算  
                for (int j = i - 1; j >= i - k; j--)  
                    steps[i] += steps[j];  
        }  
        long sum = 0;  
        for (int i = n - k; i <= n - 1; i++)  
            sum += steps[i];  
        return sum;  
    }   

原文链接：http://my.oschina.net/spance/blog/229477