在本章中你将学到:
- 推荐系统是如何工作的?
- 社会化过滤是如何工作的?
- 如何计算物品之间的相似度?
- 曼哈顿距离,欧式距离和闵科夫斯基距离
- 皮尔森相关度
- 余弦相似度
- 实现Python版本的KNN算法
- 附加的数据集
2.1 我喜欢你喜欢的
我们将通过对推荐系统的研究来开始数据挖掘的探索之旅。如今推荐系统无处不在——从Amazon到last.fm的音乐和演唱会推荐:
在上面的Amazon的例子中,Amazon融合了两种的信息来进行推荐。***个是我看过的Gene Reeves翻译的《The Lotus Sutra》;第二个是看过《The Lotus Sutra》翻译版的人看还过其他的几个翻译。
在这章中,我们介绍的推荐方法叫协同过滤。之所以称为协同,是因为它产生的 推荐是基于其他人的结果——在效果上,其实就是人们一起协作而提出推荐。它是这么工作的:假设我的任务是给你推荐一本书,我在这个网站上搜索跟你在读书方 面有相似偏好的用户。一旦发现这样的用户我就可以把她喜欢的书推荐给你——有可能是Paolo Bacigalupi的《The Windup Girl》。
2.2 如何找到那些跟你相似的人
因此***步便是那些跟你相似的人。这里有一个简单的二维空间示例,假设用户在5***评分系统中对书进行打分——0星意味着这本书很差,5星则是非常 好。因为我们是在简单二维条件下,我们把评分限制在这两本书:Neal Stephenson的《Snow Crash》和Steig Larsson的《The Girl with the Dragon Tattoo》。
首先,下列表格列出了三个用户对这两本书的评分:
我想要给神秘的X女士推荐一本书,她给《Snow Crash》评了4星,同时给《The Girl with the Dragon Tattoo》评了2星。***个任务是找到与X女士最相似、或者最相近的人。我通过计算距离来实现。
曼哈顿距离
最容易的计算距离的方法叫曼哈顿距离或者出租车距离。在2D的例子中,每个人用点(x, y)来表示。我将为每个x和y添加下标用于标示不同的人,因此(x1, y1)可能是Amy,(x2, y2)可能是难以捉摸的X女士。曼哈顿距离的计算如下:
|x1 - x2| + |y1 - y2|
(即x的差的绝对值加上y的差的绝对值)。所以Amy和X女士的曼哈顿距离是4:
计算出X女士与所有三个人的距离如下:
Amy是最相近的匹配。我们查看她的历史评分,例如,她给Paolo Bacigalupi的《The Windup Girl》评了5星,我们就可以把这本书推荐给X女士。
#p#
欧式距离
曼哈顿距离的一个优点是计算速度快。如果我们想从Facebook上的一百万用户中找出与来自Kalamazoo小Danny最相似的人,速度快是优势。
勾股定理
你可能从以前的学习中想起勾股定理,这里,我们用直线距离代替曼哈顿距离来计算Amy与X女士的距离(原本是4),直线距离如图所示:
勾股定理告诉我们如何来计算这种直线距离。
直线c表示的距离称为欧式距离,公式如下:
回顾一下,x1,x2分别表示用户1和用户2对《Dragon Tattoo》的喜好;y1,y2表示是用户1和用户2对《Snow Crash》的喜好。
Amy对《Snow Crash》和《Dragon Tattoo》都评了5分;而X女士给《Dragon Tattoo》评了2分,对《Snow Crash》评了4分。因此这两人之间的欧氏距离为:
计算X女士和所有人的欧式距离如下:
扩展到N维
我们从一开始的两本书扩展到更复杂一点的情形。假设我们在一家提供在线音乐服务的公司工作,我们想通过乐队推荐系统来获得更好的用户体验。用户可以 在我们的1-5星系统中为乐队评分,他们可以给出半颗星的评分(比如,你可以给一个乐队评2.5星)。下面的图表展示了8个用户对8个乐队的评分:
表格里的连字符"-"表示对应的用户没有给相应的乐队评分。现在我们需要通过用户对共同的乐队的打分来计算他们之间的距离。比如,当我们在计算 Angelica和Bill之间的距离时,用到乐队有Blues Traveler , Broken Bells , Phoenix, Slightly Stoopid, and Vampire Weekend。所以计算的曼哈顿距离如下:
对于行"Manhattan Distance", ***一列只需要将列"Difference"求和即可:
(1.5+1.5+3+2+1) = 9计算欧式距离的过程类似,我们只用到他们共同评过分的那些乐队:
更详细的计算如下:
动手试试
题目1:计算上表中Hailey和Veronica的欧式距离?
题目2:计算上表中Hailey和Jordyn的欧式距离?
答案:
题目1:
题目2:
一个不足
当在使用这些距离的时候我们发现它存在一个不足:当我们计算Hailey和 Veronica之间的距离的时候,我们发现他们只共同给两个乐队(Norah Jones 和 The Strokes)评了分;但是,当我们计算Hailey 和 Jordyn的距离时,我们发现他们共同给5个乐队评了分。这样看起来似乎使得我们的距离度量方法出现偏斜,因为Hailey和 Veronica的距离是二维空间上计算的,而Hailey 和 Jordyn的距离是在五维空间。当没有缺失值的情况下,曼哈顿距离和欧氏距离都表现很好。处理空值在学术上是一个热门的研究方向。在本书的后面章节我们 将讨论如何来处理这个问题。现在我们只要意识到这一缺陷即可,我们还得继续我们的"***探索" —— 构建推荐系统。
推广/泛化
曼哈顿距离和欧式距离更一般的形式是闵可夫斯基距离(Minkowski Distance):
当:
- r = 1时,上式即为曼哈顿距离
- r = 2时,上式即为欧式距离
- r = 无穷大时,上式为确界距离
很多时候你会发现公式其实并不难理解。现在让我们来剖析它。当r=1,公式就简化成曼哈顿距离:
依然以贯穿本章的音乐为例,x和y代表两个人,d(x,y)表示他们之间的距离。n是x,y都评过分的乐队的数量。我们在前面已经做过计算:
列"Difference"代表评分差值的绝对值,这些绝对值加起来得到9。
当r=2,我们得到欧氏距离的公式:
需要注意的是:当r值越大,单个维度中,大的difference值对整体的difference值影响越大。
使用Python表示这些数据
Python中表示上述数据的方式很多,在这里我将用Python中的字典表示(也叫做散列表或者哈希表)
- users = {"Angelica": {"Blues Traveler": 3.5, "Broken Bells": 2.0, "Norah Jones": 4.5, "Phoenix": 5.0, "Slightly Stoopid": 1.5, "The Strokes": 2.5, "Vampire Weekend": 2.0},
- "Bill":{"Blues Traveler": 2.0, "Broken Bells": 3.5, "Deadmau5": 4.0, "Phoenix": 2.0, "Slightly Stoopid": 3.5, "Vampire Weekend": 3.0},
- "Chan": {"Blues Traveler": 5.0, "Broken Bells": 1.0, "Deadmau5": 1.0, "Norah Jones": 3.0, "Phoenix": 5, "Slightly Stoopid": 1.0},
- "Dan": {"Blues Traveler": 3.0, "Broken Bells": 4.0, "Deadmau5": 4.5, "Phoenix": 3.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 2.0},
- "Hailey": {"Broken Bells": 4.0, "Deadmau5": 1.0, "Norah Jones": 4.0, "The Strokes": 4.0, "Vampire Weekend": 1.0},
- "Jordyn": {"Broken Bells": 4.5, "Deadmau5": 4.0, "Norah Jones": 5.0, "Phoenix": 5.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 4.0},
- "Sam": {"Blues Traveler": 5.0, "Broken Bells": 2.0, "Norah Jones": 3.0, "Phoenix": 5.0, "Slightly Stoopid": 4.0, "The Strokes": 5.0},
- "Veronica": {"Blues Traveler": 3.0, "Norah Jones": 5.0, "Phoenix": 4.0, "Slightly Stoopid": 2.5, "The Strokes": 3.0}
- }
我们通过如下方式得到某个特定用户的评分:
- >>> users["Veronica"]
- {"Blues Traveler": 3.0, "Norah Jones": 5.0, "Phoenix": 4.0, "Slightly Stoopid": 2.5, "The Strokes": 3.0}
计算曼哈顿距离的代码
计算曼哈顿距离的代码如下:
- def manhattan(rating1, rating2):
- """Computes the Manhattan distance. Both rating1 and rating2 are dictionaries
- of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""
- distance = 0
- for key in rating1:
- if key in rating2:
- distance += abs(rating1[key] - rating2[key])
- return distance
为了测试这个函数:
- >>> manhattan(users['Hailey'], users['Veronica'])
- 2.0
- >>> manhattan(users['Hailey'], users['Jordyn'])
- 7.5
接下来构建一个函数找到最相似的那个人(其实它会返回一个按距离排序好的列表,最相似的人在列表的***个):
- def computeNearestNeighbor(username, users):
- """creates a sorted list of users based on their distance to username"""
- distances = []
- for user in users:
- if user != username:
- distance = manhattan(users[user], users[username])
- distances.append((distance, user))
- # sort based on distance -- closest first
- distances.sort()
- return distances
测试函数如下:
- >>> computeNearestNeighbor("Hailey", users)
- [(2.0, ''Veronica'), (4.0, 'Chan'),(4.0, 'Sam'), (4.5, 'Dan'), (5.0, 'Angelica'), (5.5, 'Bill'), (7.5, 'Jordyn')]
***,我们将把这些代码整合在一起成为一个完整的推荐系统。比如我想为Hailey生成推荐结果,我会找到跟他最相似的邻居——在本例中是 Veronica。接着我会找出Veronica打过分但是Hailey没有打过分的乐队,我们会假设Hailey会对该乐队的评分和Veronica对 该乐队的评分相同(至少是相似)。比如,Hailey没有给Phoenix评分,Veronica给Phoenix评了4分,所以我们将猜想Hailey 很有可能也喜欢这个乐队。下面是生成推荐结果的函数。
- def recommend(username, users):
- """Give list of recommendations"""
- # first find nearest neighbor
- nearest = computeNearestNeighbor(username, users)[0][24]
- recommendations = []
- # now find bands neighbor rated that user didn't
- neighborRatings = users[nearest]
- userRatings = users[username]
- for artist in neighborRatings:
- if not artist in userRatings:
- recommendations.append((artist, neighborRatings[artist]))
- # using the fn sorted for variety - sort is more efficient
- return sorted(recommendations, key=lambda artistTuple: artistTuple[1], reverse = True)
现在为Hailey生成推荐结果:
- >>> recommend('Hailey', users)
- [('Phoenix', 4.0), ('Blues Traveler', 3.0), ('Slightly Stoopid', 2.5)]
这跟我们的期望相符。正如我们上面所示,Hailey的最相似的邻居是Veronica,Veronica给Phoenix评了4分。我们再试试其他的:
- >>> recommend('Chan', users)
- [('The Strokes', 4.0), ('Vampire Weekend', 1.0)]
- >>> recommend('Sam', users)
- [('Deadmau5', 1.0)]
我们认为Chan喜欢The Strokes,同时预测Sam不喜欢Deadmau5.
- >>> recommend('Angelica', users)
- []
对Angelica来说,返回的空值意味着我们无法对她进行推荐。我们看看问题出在哪里:
- >>> computeNearestNeighbor('Angelica', users)
- [(3.5, 'Veronica'), (4.5, 'Chan'), (5.0, 'Hailey'), (8.0, 'Sam'), (9.0, 'Bill'), (9.0, 'Dan'), (9.5, 'Jordyn')]
Angelica的最近邻居是Veronica,他们的评分表如下:
我们看到Veronica评过的所有乐队Angelica也都有评过分。我们没有更新的评分的乐队了,因此就没有推荐结果。
我们将提出方法来改善该系统来避免这种情况的出现。
课后作业
- 实现闵可夫斯基距离函数
- 改变computeNearestNeighbor,使用闵可夫斯基作为距离计算函数。
埋怨用户
让我们看看用户评分的细节。我们可以看出当用户对乐队进行打分的时候,其打分行为差别很大:
Bill不喜欢走极端,他的评分都在2星到4星之间。Jordyn看起来喜欢所有的东西,他的评分都在4星到5星之间。Hailey的评分很极端,给出的不是1星就是4星.
这种情况下,我们应该如何比较用户,比如Hailey和Jordan?Hailey的4分相当于Jordyn的4分还是5分?我想应该是更像5分,这种差异会给推荐系统带来新的问题。
皮尔森相关系数
有一种解决此类问题的方法是使用皮尔森相关系数。首先,从一般性出发,考虑下面的数据(和前面用的数据不同):
这个例子在数据挖掘领域被称为“分数通胀”。Clara的***评分是4——她的所有评分都在4到5之间。如果我们将上表中的评分用图表示:
事实上这条直线暗示着Clara和Robert之间是兴趣是高度一致的。他们都觉得Phoenix是***的乐队,其次是Blues Traveler,接着是Norah Jones。
还不错的的一致性:
不是太好的一致性:
因此从图表中可以看出:一条直线表示高度相关。皮尔森相关系数是一种度量两个变量相关性的方法(在这个例子中,Ckara和Robert的相关 性)。它的取值范围在-1到1之间。1表明完全相关,-1表明完全负相关。一个比较直观的感觉:上图中,直线的皮尔森系数是1,我标着“还不错的的一致 性”皮尔森系数有0.91,“不是太好的一致性”的系数则为0.81,所以我们可以用这个去发现与我们兴趣最相似的人。
皮尔森相关系数的公式是:
除了看起来复杂,这个公式的另外一个问题是需要对数据进行多轮运算。庆幸的是,对我们做算法的人来说,该公式有另外一个近似的形式:
(记住我两段前说过的,不要跳过公式)这个公式,除了一看是看上去更加复杂,更重要的是,数值的不稳定性意味着小的误差可能会被近似后的公式放大。 但是这个变形有一个***的好处是我们可以通过对数据一轮的遍历就能实现它。首先,我们来剖析这个公式,并结合前几页讲到的例子:
我们先计算:
这是相似度计算公式分子的***部分,这里的x和y分别代表着Clara和Robert。
对于每一个乐队,我们把Clara和Robert的分数相乘,然后求和:
接着我们计算分子的另外一部分:
因此:
等于Clara所有评分的和,即22.5. 对于Robert,其评分的和为15,他们总共对5个乐队评分,即:
因此前文中的公式的分子为70 - 67.5=2.5.
现在我们开始计算分母:
首先:
前面我们已经计算过Clara的评分之和等于22.5,平方以后得506.25。然后除以共同评分的乐队数5,得到101.25。把以上结果整合到一起得到:
接着,按照同样的方法计算Robert:
把所以的计算整合到一起得到***的结果:
因此1意味着Clara和Robert是完全相关的。
课后作业
在进行下面的计算之前,我们先使用Python实现一下Pearson相似度算法:
- def pearson(rating1, rating2):
- sum_xy = 0
- sum_x = 0
- sum_y = 0
- sum_x2 = 0
- sum_y2 = 0 !
- n = 0
- for key in rating1: !
- if key in rating2:
- n += 1
- x = rating1[key]
- y = rating2[key]
- sum_xy += x * y
- sum_x += x
- sum_y += y
- sum_x2 += x**2
- sum_y2 += y**2
- # now compute denominator
- denominator = sqrt(sum_x2 - (sum_x**2) / n) * sqrt(sum_y2 -(sum_y**2) / n)
- if denominator == 0:
- return 0
- else:
- return (sum_xy - (sum_x * sum_y) / n) / denominator
***一个公式 —— 余弦相似度
我接着讲***一个公式——余弦相似度,它在文本挖掘中非常流行,同时在协同过滤中也被广泛采用。要知道我们什么时候会用到这个公式,我们先把我们的例子做一些小小的改
变。我们记录下每个人播放某首歌曲的次数,并且以此信息来作为我们推荐算法的基础信息。
肉眼观察上面的图表(或者用上面讲到的距离公式),在听音乐的习惯上,Ann要比Ben更像Sally。
问题出现哪里?
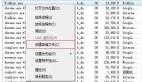
我是我iTunes中差不多有四千首歌曲,这里是播放量排名靠前的一些歌曲:
所以我的排名***的是Marcus Miller的Moonlight Sonata,总共播放25次,你有可能一次也没听过这首歌。实际上,很有可能这些排名靠前的歌曲你一首也没听过。此外,iTunes上面有超过1千5百 万首歌曲,我只有4000首。所以对某个人来说,他的数据是稀疏的,因为他只听了所有歌曲中极少的部分,每个人的播放数据是极度稀疏的。当我们在1千5百 万首歌曲里面对比两个人的音乐播放次数时,基本上他们都共同的播放的歌曲数为0。但是,当我们计算相似性的时候没法使到这种共享为0次的播放。
另外一个类似的情形是使用词计算文本之间的相似度。假设我们都喜欢一本书,比如Carey Rockwell的Tom Corbett Space Cadet:The Space Pioneers,我们想要找到类似的书本。其中一种可能的方法是使用词频。属性是某个词,属性的值是该词在书本中出现的频率。所以《The Space Pioneers 》中6.13%的词是the,0.89%是Tom,0.25%是space。我可以用这些词汇频率来计算这本书与其他书的相似度。但是,数据稀疏性问题在 这里出现了,这本书中总共有6629个不重复的词汇,而英文中有超过一百万个英文单词。所以如果我们的属性是英语单词,在《The Space Pioneers》中或者其他书本中将会有相对少的非零属性值。问题再次出现,任何相似性度量不应该依赖共有的零值。
余弦相似度忽略了0与0的匹配,其定义如下:
其中"."表示向量x和向量y的内积,"||x||"表示向量x的长度,即:
用一个例子来表示:
两个向量为:
x=(4.75, 4.5, 5, 4.25, 4) y=(4, 3, 5, 2, 1)因此:
内积为:
x⋅y = (4.75 × 4)+ (4.5 × 3)+ (5 × 5)+ (4.25 × 2)+ (4 ×1) = 70因此,余弦相似度为:
余弦相似度中,1表示完全正相关,-1表示完全负相关,因此0.935表示正相关性很高。
练习:
计算Angelica和Veronica的余弦相似度。