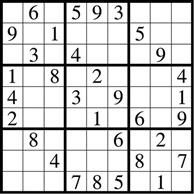
数独(Sudoku)是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫内的数字均含1-9,不重复。 每一道合格的数独谜题都有且仅有唯一答案,推理方法也以此为基础,任何无解或多解的题目都是不合格的。
如下图所示,就是一个数独的题目
关于数独的详细介绍,参看“百度百科——数独”
数独的基本解法就是利用规则的摒弃法
一些定义
每一行称为数独的行,每一列称为数独的列,每一个小九宫格称为数独的宫。数独的基本规则就是每一行、每一列、每一宫中,1-9这9个数字都只出现一次。
用(行,列)表示上图的单元格,例如(1,1)表示第一行第一列的单元格,(2,4)表示第二行第四列的单元格
如上图,每个空白单元格中能填的数字都是有限制的。
例如:(1,1)就只能填7和8;而(6,4),只能填8;
那些只能填一个数字的空白单元格,我们称之为唯一数单元格,上图中(6,4)就是唯一数单元格
解题的顺序,就是从唯一数单元格开始,由于唯一数单元格只能填一个数,故先在这个单元格里填数。在这个单元格里填数,由于规则的定义,那么这个单元格所在的行、所在的列、所在的宫的其他单元格就不能再填这个数了。这些单元格能填的数的可能性就少了。有可能会产生新的唯一数单元格。
在相当的一些的数独题目中,从唯一数单元格开始填数,不停的在唯一数单元格填数就可以把数独解出来。
如果在解题的过程中,发现某些空白单元格没有数字能填这样的单元格称之为无解单元格,那就说明:要么这个数独没有解;要么之前的解题过程有问题,需要返回检查之前的解题过程查看。
但是还有不少的数独的题目,在解题的过程中,在还有空白单元格的情况下,却找不到唯一数单元格,也就是意味着每个空白单元格中能填的数字至少有2个。我们称之为无唯一数单元格的状况
这个时候怎么办?我们找到其中一个可能数最少的空白单元格(这个没有定论,可以是可能数最少的空白单元格;也可以是第一个空白单元格;也可以是可能数最多的空白单元格,选哪个空白单元格对后面的解题是否有影响,没有证明过,不好妄下定论。凭感觉选可能数最少的空白单元格是最好的选择),由于能填的数字不止一个,先把当前的状态保存起来,再在能选的数字中选择一个数字填写(从小到大选择),然后继续求解下去。如果能解出最后的结果,说明当前的选择是正确的;如果后面的求解过程有问题,说明当前的数字的选择有问题,那么再挑选另一个数填写,继续求解。如果,所有的选择都求不出最后的结果,还是说明:要么这个数独没有解;要么之前的解题过程有问题,需要返回检查之前的解题过程查看。如此反复,直到求出最终的答案。
会有种极端的情况(可能性不大)。那就是在当前的空白单元格的所有可能的数字都选择了一遍,都没有解。而之前又没有出现无唯一数单元格的状况。那就说明这个数独根本就没有解
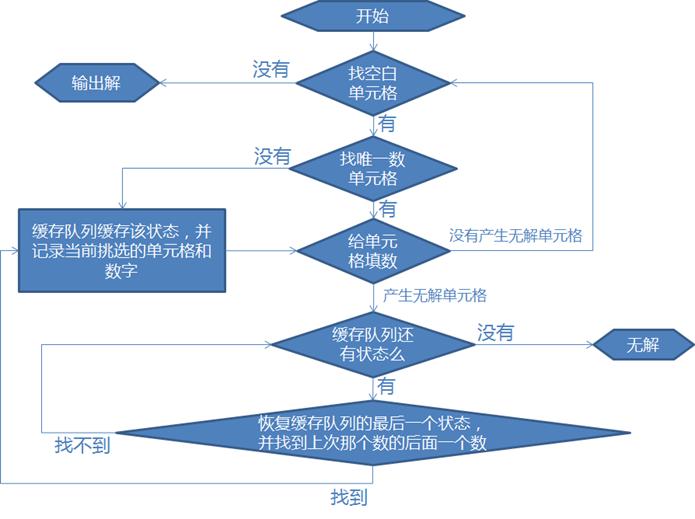
下图是数独求解的流程图
下面谈谈该算法的具体实现
1、数独状态的表示
用计算机来求解数独。基本的一点就是如何表示数独的状态。
用整形一维数组来表示数独的状态
用Num(80)表示数独的状态(数组的下标从0开始),数独是一个二维表格,而数组是一维数组。那么就存在一维和二维之间的转换
一维数组的下标Index(小标从0开始)和二维下标X、Y(下标从0开始)之间的转换公式
- 一维到二维的转换
- X=Int(Index/9)
- Y=Index mod 9
- 二维到一维的转换
- Index=X*9+Y
数组中的每个整数表示数独对应的单元格的状态
正数表示空白单元格能填的数的组合,用二进制表示。用位来表示该单元格是否能填相应的数字,1表示能填,0表示不能填。
如文章开始的数独的单元格(1,1)可能填7和8,则第7位和第8位上是1(位数是从后往前数),其余位都是0,用整数表示就是Num(0)=0110000002=192
每在单元格中填一个数字,则把相应的行、列、宫中其余的单元格把该数字去掉。
我们可以充分利用位运算来简化去数字的过程。如:要把单元格去掉7这个数字的可能。首先7对应的二进制位0010000002,取其反数得到1101111112,再和目标单元格的数值进行AND的位运算,来实现去除该单元格7这个数字的可能性(由于位运算的便捷,不需要考虑该单元格是否原本包含7这个数字的可能性)。
如:(1,1)=0110000002 AND 1101111112=0100000002,去除7这个可能性,只剩8这个可能性了,也就是成为唯一数单元格
再比如:(1,9)=0100000102 AND 1101111112=0100000102,原本单元格就没有7这个可能性,执行位运算后,还是原来的可能性,没有发生变化。
负数表示该单元格已经确定的数,例如:(1,2)=-6,表示该单元格已近填了数字6
0表示该单元格既没有填确定的数字,也没有可填数的可能性。也就是上文说的无解单元格
为了算法中计算的方便,事先把这些二进制数都缓存起来,用一个一维的数组表示
用数组V来表示各个位对应的数字
- V(0)=0000000012=1
- V(1)=0000000102=2
- V(2)=0000001002=4
- V(3)=0000010002=8
- V(4)=0000100002=16
- V(5)=0001000002=32
- V(6)=0010000002=64
- V(7)=0100000002=128
- V(8)=1000000002=256
- V(9)=1111111112=511
数字7对应的二进制数为V(6)=0010000002=64,7的反数为V(9)-V(6)=1101111112=447
每个单元格初始的值都是V(9)=1111111112=511
2、如何获得一个单元格的可填数的个数
由于是用二进制来表示单元格的状态,那么可填数的个数就是该数字中1的个数。我们之前有一个很方便的方法快速计算一个数中1的个数,参看算法的强大——快速计算一个正二进制整数中包含多少个1。
3、状态的缓存
依据之前的说法,在碰到无唯一数单元格的情况时,要把当前的状态缓存起来。考虑到实际情况,从算法的角度上来说,用栈(先进后出)这个数据结构来实现比较合适。可以自己写一个栈的实现。但是,目前很多的编程语言都实现了基本的数据结构,提供了基本的数据结构的类和方法供我们调用。
以Visual Studio为例,它有Stack这个类,实现了栈的基本操作。有两个栈的方法:Push(压栈)——把数据写到栈里面;Pop(出栈)——把数据从栈里提出来,并删除栈中的数据。
4、代码说明
基本的变量
- Private _Num(80) As Integer
- Private _V(9) As Integer
- Private _S As System.Text.StringBuilder
- Private _HasString As Boolean
_Num数组表示数独的状态;_V数组是辅助数组,缓存常用的二进制数
_S是一个文本对象,保存数独求解的过程;_HasString是个开关变量,表示是否记录求解过程;这两个变量是辅助变量,仅仅起到记录的作用。
类的初始化
- Public Sub New(Optional ByVal HasString As Boolean = True)
- Dim I As Integer
- _V(0) = 1
- For I = 1 To 8
- _V(I) = _V(I - 1) * 2
- Next
- _V(9) = 511
- For I = 0 To 80
- _Num(I) = _V(9)
- Next
- _S = New System.Text.StringBuilder
- _HasString = HasString
- End Sub
代码的前半段生成V这个数组,_V(9)=511。后半段,初始化数独数组。由于是空白数独数组,故每个单元格的值都是_V(9)
在给定的单元格里移除某个数字的可能性代码
- Private Function RemoveNum(ByVal Row As Integer, ByVal Col As Integer, ByVal Num2 As Integer) As Integer
- Dim Index As Integer = Row * 9 + Col
- If _Num(Index) > 0 Then _Num(Index) = _Num(Index) And Num2
- Return _Num(Index)
- End Function
3个参数,Row表示行,Col表示列(都是下标从0开始),Num2表示要去除的数的反码,以二进制表示。
例如:在(1,1)这个单元格去除7这个可能性,则调用RemoveNum(0,0,1101111112)
返回值是该单元格的状态值,如果返回0,表示该单元就成了无解单元格,要后面的代码做适当的处理
在给定的单元格填某个数的代码
- Private Function SetNumPri(ByVal Row As Integer, ByVal Col As Integer, ByVal Num As Integer) As Boolean
- If (_V(Num) And _Num(Row * 9 + Col)) = 0 Then Return False
- _Num(Row * 9 + Col) = -(Num + 1)
- Num = _V(9) - _V(Num)
- Dim I As Integer, J As Integer
- For I = 0 To 8
- If RemoveNum(I, Col, Num) = 0 Then Return False
- If RemoveNum(Row, I, Num) = 0 Then Return False
- Next
- Dim R1 As Integer = Int(Row / 3) * 3
- Dim C1 As Integer = Int(Col / 3) * 3
- For I = R1 To R1 + 2
- For J = C1 To C1 + 2
- If RemoveNum(I, J, Num) = 0 Then Return False
- Next
- Next
- Return True
- End Function
3个参数,Row表示行,Col表示列,Num表示要填充的数字(下标从0开始),这个方法是供类内部调用,从程序的角度来说,程序处理下标,从0开始比从1开始要来得简单。
例如:在(1,1)中填入数字7,则调用SetNumPri(0,0,6)
代码的第1行,先利用位运算判断当前单元格能否填制定的数字,不能填返回False
代码的第2行,设置当前单元格为指定数字,之前说了,用负数表示已填好的数字
代码的第3行,获得当前数字的反码,为后面去除该单元格所在的行、列、宫的其他单元格的该数字做准备
后面有两个循环,第一个循环去除行、列的其他单元格的该数字;第二个双循环去除宫的其他单元格的该数字。在调用RomoveNum方法时,若返回的是0,说明产生了无解单元格,那说明在这个单元格填该数字是不合理的,故返回False
当全部的代码都能顺利完成了,说明这个单元格填该数字是合理的,返回True
该方法的另一个重载形式
- Private Function SetNumPri(ByVal Index As Integer, ByVal Num2 As Integer) As Boolean
- Dim Row As Integer = Int(Index / 9)
- Dim Col As Integer = Index Mod 9
- Dim I As Integer
- For I = 0 To 8
- If _V(I) = Num2 Then Exit For
- Next
- Return SetNumPri(Row, Col, I)
- End Function
这也是一个供内部调用的方法,两个参数,Index是一维数组的下标;Num2是数字的二进制的形式。整个方法就是参数的转换,然后调用之前的方法
下面是两个供外面调用的方法
- Public Function SetNum(ByVal Row As Integer, ByVal Col As Integer, ByVal Num As Integer) As Boolean
- Return SetNumPri(Row - 1, Col - 1, Num - 1)
- End Function
- Public Function SetLine(ByVal Row As Integer, ByVal ParamArray Num() As Integer) As Boolean
- If Num.Length = 0 Then Return True
- Dim I As Integer
- For I = 0 To IIf(Num.Length - 1 > 8, 8, Num.Length - 1)
- If Num(I) > 0 AndAlso SetNumPri(Row - 1, I, Num(I) - 1) = False Then Return False
- Next
- Return True
- End Function
第一个方法是公开给外部调用的填数的方法。对外来说,从直观性上来说,下标是从1开始比较合适,但是内部的方法从0开始比较好。
如在(1,1)填7,调用SetNum(1,1,7),这个方法转而调用SetNumPri(0,0,6)
这个方法一般用在初始化数独时候调用
第二个方法也是公开给外部的方法,一次填写一行数的方法,如果是空白单元格,则用0替代
如本文开始的数独,填写第一行代码就是SetLine(1,0,6,0,5,9,3,0,0,0)
#p#
几个辅助方法
- Private Sub RestoreNum(ByVal L As List(Of Integer))
- Dim I As Integer
- For I = 0 To 80
- _Num(I) = L.Item(I)
- Next
- AppendString("Restore Matrix")
- End Sub
恢复L中的数据到数独数组中,L是之前缓存的数据。AppendString这个方法是将数据记录到文本对象
- Private Function Get1Count(ByVal Value As Integer) As Integer
- Dim C As Integer = 0
- Do While Value > 0
- Value = Value And (Value - 1)
- C += 1
- Loop
- Return C
- End Function
获得一个数中1的个数,也就是获得一个空白单元格的可填数的数目
例如:(1,1)=0110000002,Get1Count(0110000002)=2,说明(1,1)这个单元格能填2个数
- Private Function GetIndexOfNum(ByVal Num As Integer, ByVal Index As Integer) As Integer
- Dim I As Integer, K As Integer = 0
- For I = 0 To 8
- If (_V(I) And Num) <> 0 Then
- K += 1
- If K = Index Then Return I + 1
- End If
- Next
- Return -1
- End Function
获得指定数Num(二进制形式)的第Index个的可填数
还是以上面的为例,(1,1)=0110000002,
GetIndexOfNum(0110000002,1)=7,表示第1个可填数是7
GetIndexOfNum(0110000002,2)=8,表示第2个可填数是8
GetIndexOfNum(0110000002,3)=-1,表示没有第3个可填数
辅助记录函数
这些函数对求解算法没啥太大的帮助,仅仅是将求解的过程记录到文本中,以供日后研究参考
- Private Function ReturnNumString(ByVal Num As Integer) As String
- If Num < 0 Then Return "#" & (-Num) & " "
- Dim I As Integer, S As String = ""
- For I = 0 To 8
- If (_V(I) And Num) <> 0 Then S &= (I + 1)
- Next
- Return S.PadRight(10)
- End Function
返回一个数字的文本格式,如果是空白单元格,返回该单元格的所有可填数;如果是已填单元格,返回#+数字的字符串。返回的字符串经过对齐处理。
- Private Function ReturnMatrix() As String
- Dim I As Integer, J As Integer, S As String = ""
- For I = 0 To 8
- For J = 0 To 8
- S &= ReturnNumString(_Num(I * 9 + J))
- Next
- S &= vbNewLine
- Next
- Return S
- End Function
返回整个数独的状态文本
- Private Sub AppendString(ByVal Text As String, Optional ByVal AppendMatrix As Boolean = True)
- If _HasString = False Then Exit Sub
- _S.AppendLine(Text)
- _S.AppendLine()
- If AppendMatrix = True Then
- _S.AppendLine(ReturnMatrix)
- _S.AppendLine()
- End If
- End Sub
将文本添加到文本对象,并根据AppendMatrix参数来决定是否将整个数独的状态添加到文本对象
- Private Function IndexToXY(ByVal Index As Integer) As String
- Return (Int(Index / 9) + 1) & "-" & (Index Mod 9 + 1) & " Num:" & -_Num(Index)
- End Function
返回指定Index的坐标和已填的数,用于在文本对象中
- Public Function CalculationString() As String
- Return _S.ToString
- End Function
对外公开的方法,返回文本对象,也就是之前记录的求解过程,共日后研究参考
主求解函数——算法的核心
下面的3个函数是算法的核心
- Private Function FindMinCell() As Integer
- Dim I As Integer, C As Integer
- Dim tP As Integer = -1, tMin As Integer = 20
- I = 0
- Do
- If _Num(I) > 0 Then
- C = Get1Count(_Num(I))
- If C = 1 Then
- If SetNumPri(I, _Num(I)) = False Then Return -2
- AppendString("SetNum " & IndexToXY(I))
- If I = tP Then
- tP = -1
- tMin = 20
- End If
- I = -1
- Else
- If C < tMin Then
- tP = I
- tMin = C
- End If
- End If
- End If
- I += 1
- Loop Until I > 80
- Return tP
- End Function
该函数是获得最少可能数的单元格(可填数大于2的空白单元格)
该函数返回值有3个可能性
返回值:-1,没有找到这样的单元格,函数从某个唯一数单元格开始填数,依次填下去,并且把所有的空白单元格都填满。这说明,求解结束。
返回值:-2,没有找到这样的单元格,函数从某个唯一数单元格开始填数,依次填下去,产生了无解单元格。说明之前的求解过程有错误或者说该数独无解
返回值:0-80,找到这样的单元格,并且当前的数独数组中不再存在唯一数单元格(函数直接会在唯一数单元格上填数)
- Public Function Calculate() As Integer()
- Dim I As Integer
- Dim K As Integer
- Dim Q As New Stack(Of List(Of Integer))
- Dim L As List(Of Integer)
- _S = New System.Text.StringBuilder
- AppendString("Init Matrix")
- K = FindMinCell()
- Do While K <> -1
- If K = -2 Then
- If Q.Count = 0 Then
- AppendString("Error!!!!!", False)
- Return Nothing
- End If
- L = Q.Pop
- K = L(82)
- L.RemoveAt(82)
- I = L(81) + 1
- L.RemoveAt(81)
- AppendString("Stack Pop " & Q.Count + 1, False)
- RestoreNum(L)
- K = FindNextK(Q, L, K, I)
- Else
- L = New List(Of Integer)
- L.AddRange(_Num)
- K = FindNextK(Q, L, K, 1)
- End If
- Loop
- AppendString("Calculating Complete!!!!")
- Dim V(80) As Integer
- For I = 0 To 80
- V(I) = -_Num(I)
- Next
- Return V
- End Function
对外公开的主求解函数,返回最终结果的整形数组
首先解释一下栈对象Q,由于栈Q每次压栈的时候只能压一个对象,而当出现无唯一数单元格的情况的时候,需要将当前的数据缓存起来。需要缓存的内容有三个部分,分别是数独数组、找到的最少可能数的单元格的下标、最少可能数的单元格的选择填的第几个数。故用一个 List(of Integer)对象将之前的三个内容缓存起来。L(0)—L(80)表示是数独数组,L(81)是最少可能数的单元格的下标,L(82)是最少可能数的单元格的选择填的第几个数。
该函数的主要是判断K的值,如上个函数所述,K的值主要有3种
K=-1,说明没有空白单元格,数独已经完美的求解完成,直接返回结果
K=-2,说明有无解单元格,那么判断栈Q中的数据,如果栈Q中没有数据,说明该数独无解;如果栈Q中有数据,那么把数据提出来,把数独的状态恢复到之前的情况。并从上次缓存的最少可能数单元格中,提取下一个可填数去继续进行尝试。
举例说明,缓存了0,1。说明上次尝试的是第1个单元格(下标从0开始)的第1个可填数。由于出现了无解单元格,说明第1个可填数是不正确的,那么继续尝试第2个可填数。调用的方法:FindNextK(Q, L, K, I),之前I已经加过1了。
K=0-80,得到最少可能数的单元格的下标。从该单元格的第1个可填数开始尝试。调用的方法:FindNextK(Q, L, K, 1)
尝试可能数的函数是FindNextK,返回值也是分为3种,-1、-2、0-80。意义和上面一样
- Private Function FindNextK(ByVal Q As Stack(Of List(Of Integer)), ByVal L As List(Of Integer), ByVal K As Integer, ByVal Index As Integer) As Integer
- Dim J As Integer = GetIndexOfNum(_Num(K), Index)
- Do While J <> -1
- If SetNumPri(K, _V(J - 1)) = True Then
- AppendString("Stack Push " & Q.Count + 1, False)
- AppendString("SetNum MayBe " & IndexToXY(K))
- L.Add(Index)
- L.Add(K)
- Q.Push(L)
- K = FindMinCell()
- Exit Do
- End If
- RestoreNum(L)
- Index += 1
- J = GetIndexOfNum(_Num(K), Index)
- Loop
- If J = -1 Then K = -2
- Return K
- End Function
辅助函数,获得尝试可能数的结果
首先,通过GetIndexOfNum获得当前可填数。如果返回值-1的话,说明当前已经没有可填数,出现无解单元格,直接返回值为-2
然后尝试在当前单元格填数,调用SetNumPri(K, _V(J - 1)),返回True表示该数能填,那么把当前的状态缓存到栈Q中,并通过FindMinCell函数获得下一个可能的K值,并返回;返回False表示该数不能填,恢复数据到数独数组,继续尝试下一个数。
至此该算法类的代码都说明完整了
在该算法中仅仅用了最基本的解法——摒除法。遇见唯一数单元格,就直接填数,如果遇见无唯一数单元格,则缓存数据,并对该单元格的所有可填数做尝试,直到求解出该数独为止。
会有人疑问,利用栈Q缓存数据,会不会极大的占用系统资源,导致无法解题的情况。以目前的情况来看,我用该算法求解了“程序员们都是不被世人所理解的真正天才吗?-请大家看这个数独的解法”中的号称最难的数独,并把求解的结果保存到文件后打开分析了一下,发现栈Q的缓存不超过20步,以20步为例,每步83*4字节,则一共20*83*4=6640字节<7K字节。远小于系统的承受能力。因此,不必担心系统的承受能力
如果,谁有好的数独的算法,欢迎交流,不吝赐教。
让我们实战看看成果,用该算法求解本文开头的数独,代码如下:
- Dim tS As New clsSudoku
- tS.SetLine(1, 0, 6, 0, 5, 9, 3, 0, 0, 0)
- tS.SetLine(2, 9, 0, 1, 0, 0, 0, 5, 0, 0)
- tS.SetLine(3, 0, 3, 0, 4, 0, 0, 0, 9, 0)
- tS.SetLine(4, 1, 0, 8, 0, 2, 0, 0, 0, 4)
- tS.SetLine(5, 4, 0, 0, 3, 0, 9, 0, 0, 1)
- tS.SetLine(6, 2, 0, 0, 0, 1, 0, 6, 0, 9)
- tS.SetLine(7, 0, 8, 0, 0, 0, 6, 0, 2, 0)
- tS.SetLine(8, 0, 0, 4, 0, 0, 0, 8, 0, 7)
- tS.SetLine(9, 0, 0, 0, 7, 8, 5, 0, 1, 0)
- tS.Calculate()
- My.Computer.FileSystem.WriteAllText("1.txt", tS.CalculationString, False)
该数独还是比较简单的,一路唯一数单元格到底
结果如下:
Calculating Complete!!!!
- #7 #6 #2 #5 #9 #3 #1 #4 #8
- #9 #4 #1 #2 #7 #8 #5 #3 #6
- #8 #3 #5 #4 #6 #1 #7 #9 #2
- #1 #9 #8 #6 #2 #7 #3 #5 #4
- #4 #7 #6 #3 #5 #9 #2 #8 #1
- #2 #5 #3 #8 #1 #4 #6 #7 #9
- #3 #8 #7 #1 #4 #6 #9 #2 #5
- #5 #1 #4 #9 #3 #2 #8 #6 #7
- #6 #2 #9 #7 #8 #5 #4 #1 #3
#p#
下面是该算法类的完整代码
- Public Class clsSudoku
- Private _Num(80) As Integer
- Private _V(9) As Integer
- Private _S As System.Text.StringBuilder
- Private _HasString As Boolean
- Public Sub New(Optional ByVal HasString As Boolean = True)
- Dim I As Integer
- _V(0) = 1
- For I = 1 To 8
- _V(I) = _V(I - 1) * 2
- Next
- _V(9) = 511
- For I = 0 To 80
- _Num(I) = _V(9)
- Next
- _S = New System.Text.StringBuilder
- _HasString = HasString
- End Sub
- Private Function Get1Count(ByVal Value As Integer) As Integer
- Dim C As Integer = 0
- Do While Value > 0
- Value = Value And (Value - 1)
- C += 1
- Loop
- Return C
- End Function
- Private Function RemoveNum(ByVal Row As Integer, ByVal Col As Integer, ByVal Num2 As Integer) As Integer
- Dim Index As Integer = Row * 9 + Col
- If _Num(Index) > 0 Then _Num(Index) = _Num(Index) And Num2
- Return _Num(Index)
- End Function
- Public Function SetNum(ByVal Row As Integer, ByVal Col As Integer, ByVal Num As Integer) As Boolean
- Return SetNumPri(Row - 1, Col - 1, Num - 1)
- End Function
- Public Function SetLine(ByVal Row As Integer, ByVal ParamArray Num() As Integer) As Boolean
- If Num.Length = 0 Then Return True
- Dim I As Integer
- For I = 0 To IIf(Num.Length - 1 > 8, 8, Num.Length - 1)
- If Num(I) > 0 AndAlso SetNumPri(Row - 1, I, Num(I) - 1) = False Then Return False
- Next
- Return True
- End Function
- Private Function SetNumPri(ByVal Row As Integer, ByVal Col As Integer, ByVal Num As Integer) As Boolean
- If (_V(Num) And _Num(Row * 9 + Col)) = 0 Then Return False
- _Num(Row * 9 + Col) = -(Num + 1)
- Num = _V(9) - _V(Num)
- Dim I As Integer, J As Integer
- For I = 0 To 8
- If RemoveNum(I, Col, Num) = 0 Then Return False
- If RemoveNum(Row, I, Num) = 0 Then Return False
- Next
- Dim R1 As Integer = Int(Row / 3) * 3
- Dim C1 As Integer = Int(Col / 3) * 3
- For I = R1 To R1 + 2
- For J = C1 To C1 + 2
- If RemoveNum(I, J, Num) = 0 Then Return False
- Next
- Next
- Return True
- End Function
- Private Function SetNumPri(ByVal Index As Integer, ByVal Num2 As Integer) As Boolean
- Dim Row As Integer = Int(Index / 9)
- Dim Col As Integer = Index Mod 9
- Dim I As Integer
- For I = 0 To 8
- If _V(I) = Num2 Then Exit For
- Next
- Return SetNumPri(Row, Col, I)
- End Function
- Private Function FindMinCell() As Integer
- Dim I As Integer, C As Integer
- Dim tP As Integer = -1, tMin As Integer = 20
- I = 0
- Do
- If _Num(I) > 0 Then
- C = Get1Count(_Num(I))
- If C = 1 Then
- If SetNumPri(I, _Num(I)) = False Then Return -2
- AppendString("SetNum " & IndexToXY(I))
- If I = tP Then
- tP = -1
- tMin = 20
- End If
- I = -1
- Else
- If C < tMin Then
- tP = I
- tMin = C
- End If
- End If
- End If
- I += 1
- Loop Until I > 80
- Return tP
- End Function
- Public Function Calculate() As Integer()
- Dim I As Integer
- Dim K As Integer
- Dim Q As New Stack(Of List(Of Integer))
- Dim L As List(Of Integer)
- _S = New System.Text.StringBuilder
- AppendString("Init Matrix")
- K = FindMinCell()
- Do While K <> -1
- If K = -2 Then
- If Q.Count = 0 Then
- AppendString("Error!!!!!", False)
- Return Nothing
- End If
- L = Q.Pop
- K = L(82)
- L.RemoveAt(82)
- I = L(81) + 1
- L.RemoveAt(81)
- AppendString("Stack Pop " & Q.Count + 1, False)
- RestoreNum(L)
- K = FindNextK(Q, L, K, I)
- Else
- L = New List(Of Integer)
- L.AddRange(_Num)
- K = FindNextK(Q, L, K, 1)
- End If
- Loop
- AppendString("Calculating Complete!!!!")
- Dim V(80) As Integer
- For I = 0 To 80
- V(I) = -_Num(I)
- Next
- Return V
- End Function
- Private Sub RestoreNum(ByVal L As List(Of Integer))
- Dim I As Integer
- For I = 0 To 80
- _Num(I) = L.Item(I)
- Next
- AppendString("Restore Matrix")
- End Sub
- Private Function GetIndexOfNum(ByVal Num As Integer, ByVal Index As Integer) As Integer
- Dim I As Integer, K As Integer = 0
- For I = 0 To 8
- If (_V(I) And Num) <> 0 Then
- K += 1
- If K = Index Then Return I + 1
- End If
- Next
- Return -1
- End Function
- Private Function FindNextK(ByVal Q As Stack(Of List(Of Integer)), ByVal L As List(Of Integer), ByVal K As Integer, ByVal Index As Integer) As Integer
- Dim J As Integer = GetIndexOfNum(_Num(K), Index)
- Do While J <> -1
- If SetNumPri(K, _V(J - 1)) = True Then
- AppendString("Stack Push " & Q.Count + 1, False)
- AppendString("SetNum MayBe " & IndexToXY(K))
- L.Add(Index)
- L.Add(K)
- Q.Push(L)
- K = FindMinCell()
- Exit Do
- End If
- RestoreNum(L)
- Index += 1
- J = GetIndexOfNum(_Num(K), Index)
- Loop
- If J = -1 Then K = -2
- Return K
- End Function
- Private Function ReturnNumString(ByVal Num As Integer) As String
- If Num < 0 Then Return "#" & (-Num) & " "
- Dim I As Integer, S As String = ""
- For I = 0 To 8
- If (_V(I) And Num) <> 0 Then S &= (I + 1)
- Next
- Return S.PadRight(10)
- End Function
- Private Function ReturnMatrix() As String
- Dim I As Integer, J As Integer, S As String = ""
- For I = 0 To 8
- For J = 0 To 8
- S &= ReturnNumString(_Num(I * 9 + J))
- Next
- S &= vbNewLine
- Next
- Return S
- End Function
- Private Sub AppendString(ByVal Text As String, Optional ByVal AppendMatrix As Boolean = True)
- If _HasString = False Then Exit Sub
- _S.AppendLine(Text)
- _S.AppendLine()
- If AppendMatrix = True Then
- _S.AppendLine(ReturnMatrix)
- _S.AppendLine()
- End If
- End Sub
- Private Function IndexToXY(ByVal Index As Integer) As String
- Return (Int(Index / 9) + 1) & "-" & (Index Mod 9 + 1) & " Num:" & -_Num(Index)
- End Function
- Public Function CalculationString() As String
- Return _S.ToString
- End Function
- End Class