数据结构中二叉树的基本操作-数据结构二叉树

二叉树的基本操作，可能包括：

创建，遍历，转化，复制，删除等。

遍历：前中后三种顺序的遍历，已经是各数据结构与算法教程的最基础内容，在此不重复。

创建：大多数据结构教程当中的二叉树创建程序，都是采用的递归方式，递归方式创建的二叉树与遍历的过程相似，所创建的二叉树，也是采用左右子节点方式，后续进行遍历操作十分方便。

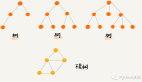
转化：直觉上，最简单的二叉树存储方式其实是如下图的数组：

*此图出自某高校数据结构ppt，但实在难以查证是哪个学校，无法直接感谢，请谅解。

首先，提供个满二叉树大小的数组，然后其中数值按完全二叉树存储。

显然，此种顺序存储方法：第i号（这里编号指对应的完全二叉树的位序）结点的左右孩子一定保存在第2i及2i+1号单元中。

故此，为兼顾存储的直观与遍历等操作的方便，从顺序数组向左右子节点存储方式的转化也就十分重要。

1-转化方法

分为几个步骤：

（1）准备原始数组

（2）分析数组中的有效值，对应二叉树节点非空；

（3）创建二叉树节点；

（4）计算除最后一层子节点外，构造节点间父子关系时的循环次数；

（5）构造二叉树节点间的父子关系；

（6）确实二叉树根节点；

主要代码：

（1）准备原始数组

//原始数组 
    int intBiTreeInit[ARR_COUNT]; 
 
    
    //初始化原始数组至无效值 
    for(int i=0;i<=ARR_COUNT-1;i++) 
        intBiTreeInit[i]=NVALUE; 
 
    //本if条件确保ARR_COUNT是否是的乘方-1 
    if(0==(ARR_COUNT & (ARR_COUNT+1))) 
    { 
        for(int i=0;i<=ARR_COUNT-1;i++) 
            intBiTreeInit[i]=2*(i+1); 
    } 
    else 
        return RET_ERR; 
 
    //使最后两数为无效值 
    intBiTreeInit[ARR_COUNT-1]=NVALUE; 
    intBiTreeInit[ARR_COUNT-2]=NVALUE;

（2）分析数组中的有效值

//开始获得数组中有效值位置 
   int intRel=0; 
   int intArr=0; 
   for(intArr=0;intArr<=intCount-1;intArr++) 
   { 
       if(elemArr[intArr]!=elemNValue) 
       { 
           intRel++; 
           vecIntEffPos.push_back(intArr); 
       } 
       }

（3）创建二叉树节点

//数组中有效值对应创建节点 
//同时初始化父子节点为NULL 
for(intArr=0;intArr<=intRel-1;intArr++) 
{ 
    pBiTreeTemp=(PBiTreeNode)malloc(sizeof(BiTreeNode));; 
     
    if(NULL==pBiTreeTemp)                                //判断是否有足够的内存空间 
    { 
        cout<<"Memory alloc failure"<<endl; 
        return RET_ERR; 
    } 
 
    //将有效值赋予节点 
    pBiTreeTemp->BiTreeData=elemArr[vecIntEffPos[intArr]]; 
     
    //初始化左右子节点为null,便于后续的遍历 
    pBiTreeTemp->leftChild=NULL; 
    pBiTreeTemp->rightChild=NULL; 
 
    //先存节点值 
    vecPBiTree.push_back(pBiTreeTemp);

（4）计算除最后一层子节点外，构造节点间父子关系时的循环次数

//生成父子关系时最后一层不必遍历,故理论循环上限可优化

int intSubLast=0; 
   intSubLast=intCount-(intCount+1)/2;

（5）构造二叉树节点间的父子关系

for(intArr=0;intArr<=intSubLast-1;intArr++) 
{ 
    //左右节点若存储有效值则同时创建父子关系 
    if(elemArr[intArr*2+1]!=elemNValue) 
        vecPBiTree[intArr]->leftChild=vecPBiTree[intArr*2+1]; 
         
    if(elemArr[intArr*2+2]!=elemNValue) 
        vecPBiTree[intArr]->rightChild=vecPBiTree[intArr*2+2];

（6）确实二叉树根节点

pBiTree=vecPBiTree[0];

转化为左右子节点方式存储后，则各种遍历操作按大多数教程的常规方式处理即可，如前序遍历函数：

int BiTreePreTrace(PBiTreeNode &pBiTree) 
{ 
    //条件为非空树 
    if(pBiTree) 
    { 
        cout<<"Node value="<<(pBiTree->BiTreeData)<<endl; 
         
        BiTreePreTrace(pBiTree->leftChild);    //遍历左子树 
        BiTreePreTrace(pBiTree->rightChild);    //遍历右子树 
    } 
    return RET_OK; 
}

完整程序，请见附件文件。

http://files.cnblogs.com/vbspine/cnsDSExec.rar

*上述程序在Windows7x64，VS2008环境编译运行通过

原文链接：http://www.cnblogs.com/vbspine/archive/2013/01/30/bitree.html

【编辑推荐】