三、对于效率提高的初次尝试
对于最自然的几种排序算法,数学家们开始思考如何提高排序算法的效率,可以通过数学证明出来如果想达到这个目的,必须想办法将相距较远的元素进行交换,具体原理涉及到比较一定的数学证明,因为我不是学数学出生的,所以我不能完整严谨的写出这个证明,所以,套用一句俗话吧,如果感兴趣你可以自己查阅一下资料。
希尔排序是以其发明人Shell的名字命名的。这里有个故事就是在一些书上,这个算法被称作是Shell-Metzner排序法,但是呢,这个叫做Metzner的人说“我没有为这种算法做任何事,我的名字不应该出现在算法的名字中。”有没有瞬间觉得这个Metzner实在是太伟大了?特别是在现在这个大环境下,这种人如果能多出现在高等教育上,顿时觉得中国的高等教育有希望了。作为***批冲刺突破二次时间界的算法之一,从交换距离较远的元素这个思路出发,在每一次的交换中奖待排序数列分为若干对,两两交换,但是这两个对的距离由近及远,不停地交换,看起来感觉有点抽象,那么就先从代码开始好了。
- void ShellSort(int numbers[],int array_size)
- {
- int j=0;
- for(int gap=array_size/2;gap>0;gap=gap/2)
- {
- cout<<"Sort time number "<<(j+1)<<":";
- for(int i=gap;i<array_size;i++)
- {
- int tmp=numbers[i];
- int j=i;
- for(;j>=gap&&tmp<numbers[j-gap];j-=gap)
- {
- numbers[j]=numbers[j-gap];
- }
- numbers[j]=tmp;
- }
- for (int i = 0; i < array_size; i++){
- cout<<numbers[i]<<" ";
- }
- j++;
- cout<<endl;
- }
- }
这个代码很值得研究,除去***的打印代码,这个排序里面竟然用了三次循环,重要的是虽然是三次循环但是却提高了效率!所以说,有的时候,事情不仅仅不是你看到的那样而且换一种看似不 看起来确实令人挺不可思议的,但是为什么呢,如果让我从一个最通俗的方式来解释的话,虽然这里有三个循环,但是在你会发现因为外面两个循环的原因,最里面一个循环执行的次数是很少的,另外一个原因就是这里的步长,步长不是逐个增加导致了循环次数的减少,从而使得性能的提高。
这一段话貌似还是很让人觉得略有些在装B,所以,还是结合实际的数解释一下增加点亲切感。
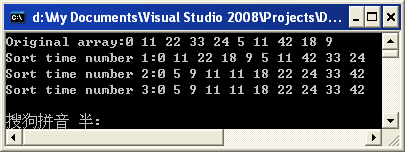
结合代码和结果来看,这里有十个数,最开始的步长是5,那么***轮分别比较(0,5),(11,11),(22,42),(33,18),(24,9),两两比较之后进行交换的结果如第二行所示,这时候最内层循环一共执行了2次,接下来,步长减半,比较的顺序应该是(0,22),(11,18),[(22,9)(进行交换)和(9,0)],[(5,18)(有交换)和(5,11)(有交换)],后面我就不列举了,实在是列举不动了,眼睛和脑子双双都不行了,在你完成全部列举完成的时候很轻松就可以看到在第三轮的时候基本上已经不需要进行交换了,这和显示出来的是一样的,这说明了在第三轮的时候最内层循环一次交换操作也没有进行,而外面两层主要是遍历,相比于交换,它所耗费的资源要少的多,换句话说,由于前面的大步长的时候进行了一些大刀阔斧的排序,导致在后面的小步长的时候只要做些许修正就可以了,有一部分情况下是完全不需要修正的,这样也得到了一个效率上的提高。
所以说增量的选择对于希尔排序能否达到提高的效果是十分重要的,这里采用的是最简单不断将步长减半的方式,一般来说,最简单的效果肯定不是***的,对于希尔排序增量选择的研究是非常多的,这个还是需要一定的数学知识的,有一种Hibbard增量可以使得希尔排序的速度达到0(N^2/3),这也是为什么希尔排序是能突破二次时间界的算法。
四、圈圈圆圆圈圈
在提高排序算法的效率上,各个大牛数学家努力的想办法减少比较次数,从而减少交换的速度,在此基础上,大牛们又发明了归并排序,快速排序的算法,使得排序的时间界达到了O(N*LOGN),而这后来也被证明了是基于交换的排序算法的时间下界。也就是说,只要你的思想离不开比较交换,排序算法的最快也就这么快了。
归并排序和快速排序的写法相对于前面的提到的要看起来“高帅富”很多,看起来非常复杂的原理用几行就写完了,而且逻辑很清晰,这一切都是得益于实现它们的时候通常都采用了递归的结构,这就像“高帅富”的跑车,先别管这个“高帅富”是否真的帅,开一个跑车出来让你看看至少已经让你在心中有了几分对于“高帅富”的敬畏,至于从车上出来的人到底是怎样的人,与他的车帅不帅关系不大。这就像用递归结构实现的算法,使用递归结构往往会使人觉得这个算法看起来很牛逼,而且可以使这个算法思想看起来十分清晰,但是至于这样实现效率是否高效,那就不一定了。
在写这两个算法之前,首先非常有必要阐述一下递归的思想,说到递归,简单的用程序的语言来解释就是不定的调用自己直到满足某一个条件结束输出某一个值或者进行某一个操作,很多人***个想到的应该是斐波那契数列,其实吧,我觉得很多书把这个作为递归思想的启蒙例子很有误导性,因为斐波那契数列的计算,如果使用递归的话,效率是非常差的,虽然这个求斐波那契数列某一项的代码很简单,我还是贴出来一下。
- int Fibonacci(int n)
- {
- if(n==0||n==1)
- return n;
- else
- return Fibonacci(n-1)+ Fibonacci(n-2);
- }
我们来测试一下它的运行时间好了,我们求前50项的值,看看它所要耗费的时间。
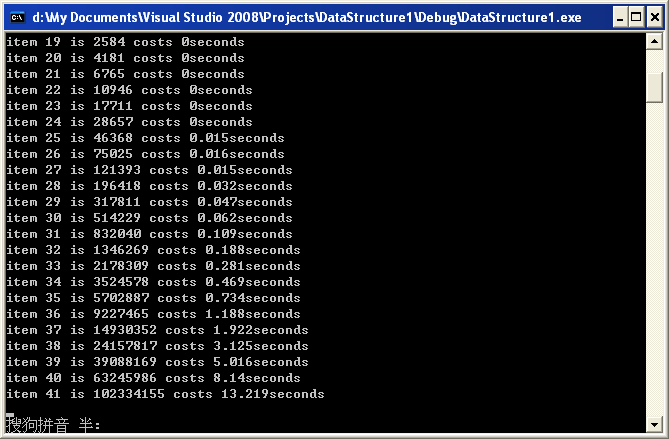
我已经等不到第50项的值出来了,从运行结果可以看到到第39项的时候运行时间已经开始飙升了,到不了第50项就已经到了无法忍受的地步了,这明显完全无法满足实际的要求,某种程度上这会给人一种误导,递归在实际运用中用处不大。明显,这种想法是错误的。
来看这样一个例子,将一个数字倒序输出,比如输入的是12345,输出是54321,这个问题的解法相当简单,就是不停将自身的对10取余,不停地数以10。这个解法符合递归的思想,其代码如下所示:
- void PrintReverse(int n)
- {
- if(n!=0)
- {
- cout<<n%10;
- PrintReverse(n/10);
- }
- }
这样的一个例子就适合用递归的思想去做,因为一个整数很少能大到拥有100位以上,所以这个递归算法的运行效率会很高,加上这个程序从上到下读下来和我前面说的基本思想非常的符合,比较符合人的逻辑思维习惯,增加了程序的可读性。所以说,递归并不是像有些书里面说的那样,效率低,一般情况下尽量不要用,任何一样东西都没有绝对的好坏,只有你有没有用到适合的地方。
***,一个经常遇到的问题是不是任何递归都能转换成为非递归的程序呢?答案是可以的,只要你运用适当的数据结构,都能转换成为非递归程序,但是转换的过程并没有那么的简单,所以将递归转换成为非递归,有时候还是需要一定的数学知识的。