先回答几个留言中的一个问题和我对无损编码那一节的一个留言的一个看法,***个是推荐算法书,首先,我不是什么高手和大牛,所以当不起“推荐”这个词。我见过很多人,对于这个问题我觉得很多人都会说出《算法导论》,但是我不完全这么认为,我始终认为人和人是不一样的,《算法导论》肯定是一本经典的书,但是学习知识的目的是要学懂,比谁的能力大不是比谁看的经典书籍多,而是比谁懂得多。所以如果让我推荐的话,我觉得要分三种情况,***种,你有很深的数学基础,高中特别喜欢做数学题,我觉得可以尝试看看《算法导论》甚至是传说中的《计算机程序设计艺术》,第二种就是高中并不对数学很感兴趣,但是大学确实很喜欢编程但是对于数学看多了觉得头会昏昏的人,其实我特别觉得好的是《算法概论》和《算法设计与分析基础》,除了这两本,我觉得看一些《离散数学》对于培养算法的基本思维方式真很有帮助,第三种是对于数学理解不是那么强的,我觉得不妨看看《编程之美》这类的有实际例子不会那么抽象的书,培养出兴趣,有了兴趣,后面只是时间问题了。
第二个是对无损编码有一个朋友说的这是“时间换空间”,从编程上说确实是时间换空间,但是这些一般都是在有实际应用背景下的,比如我的所谓研究方向是“可逆水印”,这个玩意儿必须要靠无损编码做前期处理,所以这个看法是正确的,但是却不是最需要考虑的,因为这个有应用背景。
好了,开始这次的内容,不同于很多数据结构先从列表和堆栈说起,我先几个和数据结构结合不太强的排序算法开始,因为我觉得在学这一系列之前对算法的效率建立一个认识是必要的。
二、从几种“屌丝”的排序算法开始
先介绍几种简单的时间效率是O(N*N)的排序算法,虽然这些排序算法比较初级,但是任何高级的东西都是从初级的东西演化推理出来的,不学小学的123你也不可能学会高数的微积分。所以说这些算法虽然“屌丝”,但是没有这些“屌丝”哪来的“高帅富”?可以证明的出来,通过交换的排序算法效率最快只能到O(N*logN)。
除了上面的这个,我还想强调的一点是在有的书里面提到的排序算法是否是稳定的这个概念,所谓有序就是说待排序数列中相等的值在经过排序算法之后是否会交换位置,比如一组数据(2,0,2),在排序之后自然是(0,2,2),如果这个排序算法是稳定的,那么(0,2,2)中***个出现的2应该是(2,0,2)中的***个2,也就是待排序数列中的两个2的相对位置不会发生交换。关于稳定的定义可以参看百度的这个http://baike.baidu.com/view/547325.htm?fromTaglist 这个看似不起眼的知识点就是昨天微软校园招聘倒数第二题的考点,不得不说大公司出的题目牛逼。
选择排序是最为符合人类自然思维的一种排序方式,不断找到数列中的最小值,将其放在目前最小的位置上,简单方便快捷,不得不说是最“屌丝”的排序算法,没有什么特殊的技巧,完全靠两个循环,代码如下所示:
- void SelectionSort(int a[],int length)
- {
- for(int i=0;i<length;i++)
- {
- cout<<"Sort time number "<<(i+1)<<":";
- int min=i;
- int j=i;
- for(;j<length;j++)
- {
- if(a[min]>a[j])
- min=j;
- }
- int tmp=a[min];
- a[min]=a[i];
- a[i]=tmp;
- for(int k=0;k<length;k++)
- cout<<a[k]<<" ";
- cout<<endl;
- }
- }
运行结果如下所示:

从结果中可以看到,***轮排序中,最小的元素3被安排在了***个位置上,第二轮5被安排在次小的位置上,以此类推。选择排序算法是不是稳定的呢?选择排序明显不是有序的,就像连接里面写的那样,因为你在交换的过程中,如果出现相同的元素,无法保证交换的过程中元素被交换的位置是否在第二次出现该元素之后。
接下来当然是冒泡排序,这种排序算法通过不断比较相邻两个数的大小并交换位置来达到排序的目的,这种算法比较符合人类的自然思维,这样就自然需要两个循环,***个循环是遍历整个数组,第二个循环是不停地未排序的数列中两个相邻的元素,每一轮之后,***的元素都可以排在目前***的位置(当然这取决于你的比较部分的代码是如何写的),所以这个算法也很容易写出来。
- void bubble(int a[],int length)
- {
- int temp=0;
- for(int j=0;j<length;j++)
- {
- cout<<"Sort time number "<<(j+1)<<":";
- for (int i=0;i<length-1;i++)
- if (a[i]>a[i+1])
- {
- temp=a[i];
- a[i]=a[i+1];
- a[i+1]=temp;
- }
- for(int k=0;k<length;k++)
- cout<<a[k]<<" ";
- cout<<endl;
- }
- }
其结果如下图所示:
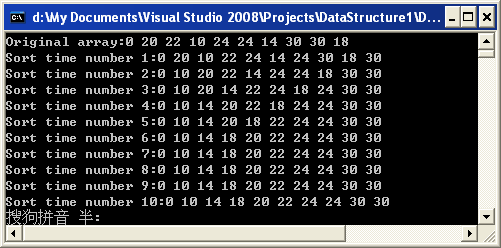
这个简单的排序算法却反应出了排序算法的一个最初级的思路就是比较和交换,别小看任何不起眼的概念,因为后面大牛们对于排序算法的改进就是通过相近办法减少比较和交换,或者是不做相邻元素的比较。可以看到每一趟排序之后,当前***的元素都到了当前***的位置上,冒泡排序算法是稳定的排序算法,但是前提是你不会在比较的过程中使用<=或者>=这种符号,交换两个相等的元素是没有意义的,加上算法一般是到大数据集中才显示出作用,这些环境下一个重要的因子就是要快,这种交换会无谓的增大程序的开销,所以一般在排序算法中不会用到=的交换,你也就不用钻牛角尖的说排序算法的稳定性会取决于用于比较的符号。
除了冒泡排序,插入排序我觉得是***人的排序自然思维方式的拓展,这个算法的思想基本就是不停地排出有序的数列,比如10个数,先将前两个数的顺序排好,再看第三个数,然后将这三个数排好,不断吸收元素,不断的排序,这样会保持了待排序数列的相对稳定性,也保持了算法排序的稳定性。其实现代码如下:
- void InsertSort(int numbers[],int array_size)
- {
- int j;
- for(int p=1;p<array_size;p++)
- {
- cout<<"Sort time number "<<p<<":";
- int tmp=numbers[p];
- for(j=p;j>0&&tmp<numbers[j-1];j--)
- {
- numbers[j]=numbers[j-1];
- }
- numbers[j]=tmp;
- for(int k=0;k<array_size;k++)
- cout<<numbers[k]<<" ";
- cout<<endl;
- }
- }
实现结果如下图所示:
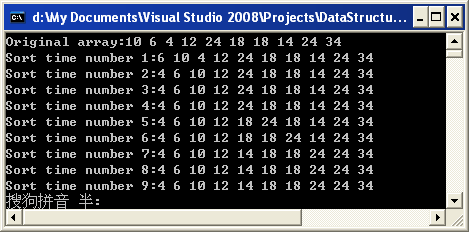
可以看到这种排序算法,吸收,排序的特点,最开始是两个元素的数组编程有序的,第二次是3个元素变成的,如此往复。
这三种最简单的排序算法是排序算法的入门,如果想测试其效率,可以使用我上一节的代码,这里我还要说一句的是,我写的这三段代码参数的命名都是不一样的,这是因为我是好几天写的,这也反过来说明了在软件开发中有一个规范的重要性,试想如果是很多人一起开发软件,一样的参数意思,你今天想到用着表示,明天想到用那个表示,对于别人这是一种莫大的痛苦。
原文链接:http://www.cnblogs.com/ZXYloveFR/archive/2012/09/23/2698563.html
【编辑推荐】