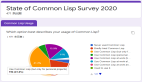
本文是paul graham所著的《Lisp之根源》的第二部分,介绍了Lisp函数的表示(***部分)。有关Lisp函数表示的具体描述如下:
函数的表示
接着我们定义一个记号来描述函数.函数表示为(lambda ( ... ) e ),其中 ... 是原子(叫做参数 ),e 是表达式. 如果表达式的***个元素形式如上
- ((lambda ( ... ) e ) ... )
则称为函数调用 .它的值计算如下.每一个表达式 先求值,然后e 再求值.在e 的求值过程中,每个出现在e 中的 的值是相应的 在最近一次的函数调用中的值.
- > ((lambda (x) (cons x '(b))) 'a)
- (a b)
- > ((lambda (x y) (cons x (cdr y)))
- 'z
- '(a b c))
- (z b c)
如果一个表达式的***个元素f 是原子且f 不是原始操作符
- (f ... )
并且f 的值是一个函数(lambda ( ... )),则以上表达式的值就是
- ((lambda ( ... ) e ) ... )
的值. 换句话说,参数在表达式中不但可以作为自变量也可以作为操作符使用:
- > ((lambda (f) (f '(b c)))
- '(lambda (x) (cons 'a x)))
- (a b c)
有另外一个函数记号使得函数能提及它本身,这样我们就能方便地定义递归函数.3 记号
- (label f (lambda ( ... ) e ))
表示一个象(lambda ( ... ) e )那样的函数,加上这样的特性: 任何出现在e 中的f 将求值为此label表达式, 就好象f 是此函数的参数.
假设我们要定义函数(subst x y z ), 它取表达式x ,原子y 和表z 做参数,返回一个象z 那样的表, 不过z 中出现的y (在任何嵌套层次上)被x 代替.
- > (subst 'm 'b '(a b (a b c) d))
- (a m (a m c) d)
我们可以这样表示此函数
- (label subst (lambda (x y z)
- (cond ((atom z)
- (cond ((eq z y) x)
- ('t z)))
- ('t (cons (subst x y (car z))
- (subst x y (cdr z)))))))
我们简记f =(label f (lambda ( ... ) e ))为
(defun f ( ... ) e )
于是
- (defun subst (x y z)
- (cond ((atom z)
- (cond ((eq z y) x)
- ('t z)))
- ('t (cons (subst x y (car z))
- (subst x y (cdr z))))))
偶然地我们在这儿看到如何写cond表达式的缺省子句. ***个元素是't的子句总是会成功的. 于是
- (cond (x y ) ('t z ))
等同于我们在某些语言中写的
- if x then y else z
对Lisp函数的表示便介绍到这里。
【编辑推荐】