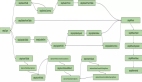
回忆一下我们的英雄所处的困境:在试图创建一个 DSL(这里只不过是一种非常简单的计算器语言)时,他创建了包含可用于该语言的各种选项的树结构:
◆二进制加/减/乘/除运算符
◆一元反运算符
◆数值
它背后的执行引擎知道如何执行那些操作,它甚至有一个显式的优化步骤,以减少获得结果所需的计算。
最后的 代码 是这样的:
清单 1. 计算器 DSL:AST 和解释器
- package com.tedneward.calcdsl
- {
- private[calcdsl] abstract class Expr
- private[calcdsl] case class Variable(name : String) extends Expr
- private[calcdsl] case class Number(value : Double) extends Expr
- private[calcdsl] case class UnaryOp(operator : String, arg : Expr) extends Expr
- private[calcdsl] case class BinaryOp(operator : String, left : Expr, right : Expr)
- extends Expr
- object Calc
- {
- /**
- * Function to simplify (a la mathematic terms) expressions
- */
- def simplify(e : Expr) : Expr =
- {
- e match {
- // Double negation returns the original value
- case UnaryOp("-", UnaryOp("-", x)) => simplify(x)
- // Positive returns the original value
- case UnaryOp("+", x) => simplify(x)
- // Multiplying x by 1 returns the original value
- case BinaryOp("*", x, Number(1)) => simplify(x)
- // Multiplying 1 by x returns the original value
- case BinaryOp("*", Number(1), x) => simplify(x)
- // Multiplying x by 0 returns zero
- case BinaryOp("*", x, Number(0)) => Number(0)
- // Multiplying 0 by x returns zero
- case BinaryOp("*", Number(0), x) => Number(0)
- // Dividing x by 1 returns the original value
- case BinaryOp("/", x, Number(1)) => simplify(x)
- // Dividing x by x returns 1
- case BinaryOp("/", x1, x2) if x1 == x2 => Number(1)
- // Adding x to 0 returns the original value
- case BinaryOp("+", x, Number(0)) => simplify(x)
- // Adding 0 to x returns the original value
- case BinaryOp("+", Number(0), x) => simplify(x)
- // Anything else cannot (yet) be simplified
- case _ => e
- }
- }
- def evaluate(e : Expr) : Double =
- {
- simplify(e) match {
- case Number(x) => x
- case UnaryOp("-", x) => -(evaluate(x))
- case BinaryOp("+", x1, x2) => (evaluate(x1) + evaluate(x2))
- case BinaryOp("-", x1, x2) => (evaluate(x1) - evaluate(x2))
- case BinaryOp("*", x1, x2) => (evaluate(x1) * evaluate(x2))
- case BinaryOp("/", x1, x2) => (evaluate(x1) / evaluate(x2))
- }
- }
- }
- }
#p#
前一篇文章的读者应该还记得,我布置了一个挑战任务,要求改进优化步骤,进一步在树中进行简化处理,而不是像清单 1 中的代码那样停留在最顶层。Lex Spoon 发现了我认为是最简单的优化方法:首先简化树的 “边缘”(每个表达式中的操作数,如果有的话),然后利用简化的结果,再进一步简化顶层的表达式,如清单 2 所示:
清单 2. 简化、再简化
- /*
- * Lex's version:
- */
- def simplify(e: Expr): Expr = {
- // first simplify the subexpressions
- val simpSubs = e match {
- // Ask each side to simplify
- case BinaryOp(op, left, right) => BinaryOp(op, simplify(left), simplify(right))
- // Ask the operand to simplify
- case UnaryOp(op, operand) => UnaryOp(op, simplify(operand))
- // Anything else doesn't have complexity (no operands to simplify)
- case _ => e
- }
- // now simplify at the top, assuming the components are already simplified
- def simplifyTop(x: Expr) = x match {
- // Double negation returns the original value
- case UnaryOp("-", UnaryOp("-", x)) => x
- // Positive returns the original value
- case UnaryOp("+", x) => x
- // Multiplying x by 1 returns the original value
- case BinaryOp("*", x, Number(1)) => x
- // Multiplying 1 by x returns the original value
- case BinaryOp("*", Number(1), x) => x
- // Multiplying x by 0 returns zero
- case BinaryOp("*", x, Number(0)) => Number(0)
- // Multiplying 0 by x returns zero
- case BinaryOp("*", Number(0), x) => Number(0)
- // Dividing x by 1 returns the original value
- case BinaryOp("/", x, Number(1)) => x
- // Dividing x by x returns 1
- case BinaryOp("/", x1, x2) if x1 == x2 => Number(1)
- // Adding x to 0 returns the original value
- case BinaryOp("+", x, Number(0)) => x
- // Adding 0 to x returns the original value
- case BinaryOp("+", Number(0), x) => x
- // Anything else cannot (yet) be simplified
- case e => e
- }
- simplifyTop(simpSubs)
- }
在此对 Lex 表示感谢。
#p#
解析
现在是构建 DSL 的另一半工作:我们需要构建一段代码,它可以接收某种文本输入并将其转换成一个 AST。这个过程更正式的称呼是解析(parsing)(更准确地说,是标记解释(tokenizing)、词法解析(lexing) 和语法解析)。
以往,创建解析器有两种方法:
手工构建一个解析器。
通过工具生成解析器。
我们可以试着手工构建这个解析器,方法是手动地从输入流中取出一个字符,检查该字符,然后根据该字符以及在它之前的其他字符(有时还要根据在它之后的字符)采取某种行动。对于较小型的语言,手工构建解析器可能更快速、更容易,但是当语言变得更庞大时,这就成了一个困难的问题。
除了手工编写解析器外,另一种方法是用工具生成解析器。以前有 2 个工具可以实现这个目的,它们被亲切地称作lex(因为它生成一个 “词法解析器”)和 yacc(“Yet Another Compiler Compiler”)。对编写解析器感兴趣的程序员没有手工编写解析器,而是编写一个不同的源文件,以此作为 “lex” 的输入,后者生成解析器的前端。然后,生成的代码会与一个 “grammar” 文件 —— 它定义语言的基本语法规则(哪些标记中是关键字,哪里可以出现代码块,等等)—— 组合在一起,并且输入到 yacc 生成解析器代码。
由于这是 Computer Science 101 教科书,所以我不会详细讨论有限状态自动机(finite state automata)、LALR 或 LR 解析器,如果需要深入了解请查找与这个主题相关的书籍或文章。
同时,我们来探索 Scala 构建解析器的第 3 个选项:解析器组合子(parser combinators),它完全是从 Scala 的函数性方面构建的。解析器组合子使我们可以将语言的各种片段 “组合” 成部件,这些部件可以提供不需要代码生成,而且看上去像是一种语言规范的解决方案。
解析器组合子
了解 Becker-Naur Form(BNF)有助于理解解析器组合子的要点。BNF 是一种指定语言的外观的方法。例如,我们的计算器语言可以用清单 3 中的 BNF 语法进行描述:
清单 3. 对语言进行描述
- input ::= ws expr ws eoi;
- expr ::= ws powterm [{ws '^' ws powterm}];
- powterm ::= ws factor [{ws ('*'|'/') ws factor}];
- factor ::= ws term [{ws ('+'|'-') ws term}];
- term ::= '(' ws expr ws ')' | '-' ws expr | number;
- number ::= {dgt} ['.' {dgt}] [('e'|'E') ['-'] {dgt}];
- dgt ::= '0'|'1'|'2'|'3'|'4'|'5'|'6'|'7'|'8'|'9';
- ws ::= [{' '|'\t'|'\n'|'\r'}];
语句左边的每个元素是可能的输入的集合的名称。右边的元素也称为 term,它们是一系列表达式或文字字符,按照可选或必选的方式进行组合。(同样,BNF 语法在 Aho/Lam/Sethi/Ullman 等书籍中有更详细的描述,请参阅 参考资料)。
用 BNF 形式来表达语言的强大之处在于,BNF 和 Scala 解析器组合子不相上下;清单 4 显示使用 BNF 简化形式后的清单 3:
清单 4. 简化、再简化
- expr ::= term {'+' term | '-' term}
- term ::= factor {'*' factor | '/' factor}
- factor ::= floatingPointNumber | '(' expr ')'
其中花括号({})表明内容可能重复(0 次或多次),竖线(|)表明也/或的关系。因此,在读清单 4 时,一个 factor 可能是一个 floatingPointNumber(其定义在此没有给出),或者一个左括号加上一个 expr 再加上一个右括号。
在这里,将它转换成一个 Scala 解析器非常简单,如清单 5 所示:
清单 5. 从 BNF 到 parsec
- package com.tedneward.calcdsl
- {
- object Calc
- {
- // ...
- import scala.util.parsing.combinator._
- object ArithParser extends JavaTokenParsers
- {
- def expr: Parser[Any] = term ~ rep("+"~term | "-"~term)
- def term : Parser[Any] = factor ~ rep("*"~factor | "/"~factor)
- def factor : Parser[Any] = floatingPointNumber | "("~expr~")"
- def parse(text : String) =
- {
- parseAll(expr, text)
- }
- }
- def parse(text : String) =
- {
- val results = ArithParser.parse(text)
- System.out.println("parsed " + text + " as " + results + " which is a type "
- + results.getClass())
- }
- // ...
- }
- }
BNF 实际上被一些解析器组合子语法元素替换:空格被替换为 ~ 方法(表明一个序列),重复被替换为 rep 方法,而选择则仍然用 | 方法来表示。文字字符串是标准的文字字符串。
从两个方面可以看到这种方法的强大之处。首先,该解析器扩展 Scala 提供的 JavaTokenParsers 基类(后者本身又继承其他基类,如果我们想要一种与 Java 语言的语法概念不那么严格对齐的语言的话),其次,使用 floatingPointNumber 预设的组合子来处理解析一个浮点数的细节。
这种特定的(一个中缀计算器的)语法很容易使用(这也是在那么多演示稿和文章中看到它的原因),为它手工构建一个解析器也不困难,因为 BNF 语法与构建解析器的代码之间的紧密关系使我们可以更快、更容易地构建解析器。
#p#
解析器组合子概念入门
为了理解其中的原理,我们必须简要了解解析器组合子的实现。实际上,每个 “解析器” 都是一个函数或一个 case 类,它接收某种输入,并产生一个 “解析器”。例如,在最底层,解析器组合子位于一些简单的解析器之上,这些解析器以某种输入读取元素(一个 Reader)作为输入,并生成某种可以提供更高级的语义的东西(一个 Parser):
清单 6. 一个基本的解析器
- type Elem
- type Input = Reader[Elem]
- type Parser[T] = Input => ParseResult[T]
- sealed abstract class ParseResult[+T]
- case class Success[T](result: T, in: Input) extends ParseResult[T]
- case class Failure(msg: String, in: Input) extends ParseResult[Nothing]
换句话说,Elem 是一种抽象类型,用于表示任何可被解析的东西,最常见的是一个文本字符串或流。然后,Input 是围绕那种类型的一个 scala.util.parsing.input.Reader(方括号表明 Reader 是一个泛型;如果您喜欢 Java 或 C++ 风格的语法,那么将它们看作尖括号)。然后,T 类型的 Parser 是这样的类型:它接受一个 Input,并生成一个 ParseResult,后者(基本上)属于两种类型之一:Success 或 Failure。
显然,关于解析器组合子库的知识远不止这些 — 即使 ~ 和 rep 函数也不是几个步骤就可以得到的 — 但是,这让您对解析器组合子的工作原理有基本的了解。“组合” 解析器可以提供解析概念的越来越高级的抽象(因此称为 “解析器组合子”;组合在一起的元素提供解析行为)。
我们还没有完成,是吗?
我们仍然没有完成。通过调用快速测试解析器可以发现,解析器返回的内容并不是计算器系统需要的剩余部分:
清单 7. 第一次测试失败?
- package com.tedneward.calcdsl.test
- {
- class CalcTest
- {
- import org.junit._, Assert._
- // ...
- @Test def parseNumber =
- {
- assertEquals(Number(5), Calc.parse("5"))
- assertEquals(Number(5), Calc.parse("5.0"))
- }
- }
- }
这次测试会在运行时失败,因为解析器的 parseAll 方法不会返回我们的 case 类 Number(这是有道理的,因为我们没有在解析器中建立 case 类与解析器的产生规则之间的关系);它也没有返回一个文本标记或整数的集合。
相反,解析器返回一个 Parsers.ParseResult,这是一个 Parsers.Success 实例(其中有我们想要的结果);或者一个 Parsers.NoSuccess、Parsers.Failure 或 Parsers.Error(后三者的性质是一样的:解析由于某种原因未能正常完成)。
假设这是一次成功的解析,要得到实际结果,必须通过 ParseResult 上的 get 方法来提取结果。这意味着必须稍微调整 Calc.parse 方法,以便通过测试。如清单 8 所示:
清单 8. 从 BNF 到 parsec
- package com.tedneward.calcdsl
- {
- object Calc
- {
- // ...
- import scala.util.parsing.combinator._
- object ArithParser extends JavaTokenParsers
- {
- def expr: Parser[Any] = term ~ rep("+"~term | "-"~term)
- def term : Parser[Any] = factor ~ rep("*"~factor | "/"~factor)
- def factor : Parser[Any] = floatingPointNumber | "("~expr~")"
- def parse(text : String) =
- {
- parseAll(expr, text)
- }
- }
- def parse(text : String) =
- {
- val results = ArithParser.parse(text)
- System.out.println("parsed " + text + " as " + results + " which is a type "
- + results.getClass())
- results.get
- }
- // ...
- }
- }
成功了!真的吗?
对不起,还没有成功。运行测试表明,解析器的结果仍不是我前面创建的 AST 类型(expr 和它的亲属),而是由 List 和 String 等组成的一种形式。虽然可以将这些结果解析成 expr 实例并对其进行解释,但是肯定还有另外一种方法。
确实有另外一种方法。为了理解这种方法的工作原理,您将需要研究一下解析器组合子是如何产生非 “标准” 的元素的(即不是 String 和 List)。用适当的术语来说就是解析器如何才能产生一个定制的元素(在这里,就是 AST 对象)。这个主题下一次再讨论。
在下一期中,我将和您一起探讨解析器组合子实现的基础,并展示如何将文本片段解析成一个 AST,以便进行求值(然后进行编译)。
结束语
显然,我们还没有结束(解析工作还没有完成),但是现在有了基本的解析器语义,接下来只需通过扩展解析器产生元素来生成 AST 元素。
对于那些想领先一步的读者,可以查看 ScalaDocs 中描述的 ^^ 方法,或者阅读 Programming in Scala 中关于解析器组合子的小节;但是,在此提醒一下,这门语言比这些参考资料中给出的例子要复杂一些。
当然,您可以只与 String 和 List 打交道,而忽略 AST 部分,拆开返回的 String 和 List,并重新将它们解析成 AST 元素。但是,解析器组合子库已经包含很多这样的内容,没有必要再重复一遍。
【相关阅读】