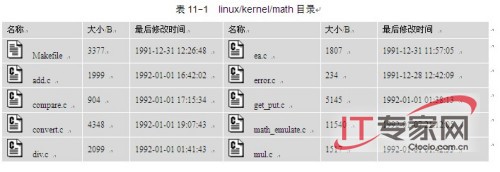
内核目录kernel/math目录中包含数学协处理器仿真处理代码文件,共包含9个C语言程序,见表11-1。本章内容与具体硬件结构关系非常密切,因此需要读者具备较深的有关Intel CPU和协处理器指令代码结构的知识。但好在这些内容与内核实现关系不大,因此跳过本章内容并不会妨碍读者对内核实现方法的完整理解。不过若能理解本章内容,那么对于实现系统级应用程序(例如汇编和反汇编等程序)和编制协处理器浮点处理程序将有很大帮助。
11.1 总体功能描述
在计算机上执行计算量较大的运算通常可以使用三种方法来完成。一种是直接使用CPU普通指令执行计算。由于CPU指令是一类通用指令,因此使用这些指令进行复杂和大量的运算工作需要编制复杂的计算子程序,并且一般只有通晓数学和计算机的专业人员才能编制出这些子程序。另一种方法是为CPU配置一个数学协处理器芯片。使用协处理器芯片可以极大地简化数学处理编程难度,并且运算速度和效率也会成倍提高,但需要另外增加硬件投入。还有一种方法是在系统内核级使用仿真程序来模拟协处理器的运算功能。这种方法可能是运算速度和效率最低的一种,但与使用了协处理器一样可以方便程序员编制计算程序,并且能够在对程序不加任何改动的情况下把所编程序运行在具有协处理器的机器上。
在Linux 0.1x甚至Linux 0.9x内核开发初期,数学协处理器芯片80387(或其兼容芯片)价格不菲,并且一直是普通PC中的奢侈品。因此除非在科学计算量很大的场合或特别需要之处,一般PC中不会安装80387芯片。虽然现在的Intel 处理器中都内置了数学协处理器功能部件,从而现在的操作系统中已经无须包含协处理器仿真程序代码,但是因为80387仿真程序完全建立在模拟80387芯片处理结构和分析指令代码结构基础上,因此学习本章内容后读者不仅能够了解80387协处理器编程方法,而且对编写汇编和反汇编处理程序也有很大帮助。
如果80386 PC中没有包括80387数学协处理器芯片,那么当CPU执行到一条协处理器指令时就会引发“设备不存在”异常中断7。该异常过程的处理代码在sys_call.s第158行开始处。如果操作系统在初始化时已经设置了CPU控制寄存器CR0的EM位,那么此时就会调用math_emulate.c程序中的math_emulate()函数来用软件“解释”执行每一条协处理器指令。
Linux 0.12内核中的数学协处理器仿真程序math_emulate.c完全模拟了80387芯片执行协处理器指令的方式。在处理一条协处理器指令之前,该程序会首先使用数据结构等类型在内存中建立起一个“软”80387环境,包括模仿所有80387内部栈式累加器组ST[]、控制字寄存器CWD、状态字寄存器SWD和特征字TWD(TAG word)寄存器,然后分析引起异常的当前协处理器指令操作码,并根据具体操作码执行相应的数学模拟运算。因此在描述math_emulate.c程序的处理过程之前,有必要先介绍一下80387的内部结构和基本工作原理。
11.1.1 浮点数据类型
本节主要介绍协处理器使用的浮点数据类型。首先简单回顾一下整型数的几种表示方式,然后说明浮点数的几种标准表示方式以及在80387中运算时使用的临时实数表示方法。
1.整型数据类型
对于Intel 32位CPU来讲,有三种基本无符号数据类型:字节(byte)、字(word)和双字(double word),分别有8、16和32位。无符号数的表示方式很简单,字节中的每个位都代表一个二进制数,并且根据其所处位置具有不同的权值。例如一个无符号二进制数0b10001011可表示为:
U = 0b10001011 = 1×27 + 0×26 + 0×25 + 0×24 + 1×23 + 0×22 + 1×21 + 1×20 = 139
它对应十进制数139。其中权值最小的一位(20)通常被称为最低有效位(LSB,Least Significant Bit),而权值最大的位(27)被称为最高有效位(MSB,Most Significant Bit)。
#p#而计算机中具有负数值的整型数据表示方法通常也有三种:2的补码(Two’s complement)、符号数(Sign magnitude)和偏置数(biased number)表示方式。表11-2给出了这三种形式表示的一些数值。
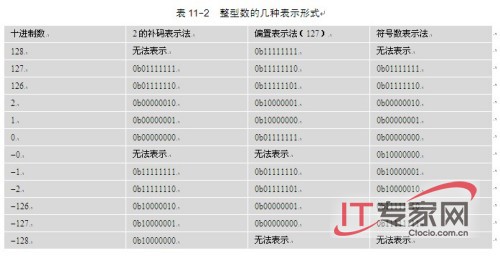
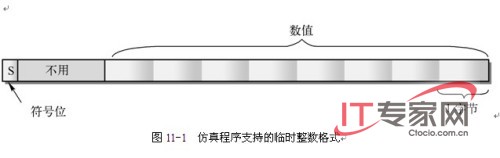
2的补码(二进制补码)表示法是目前大多数计算机CPU使用的整数表示方法,因为CPU的无符号数的简单加法也适用于这种格式的数据运算。使用这种表示法,一个数的负数就是该数每位取反后再加1。MSB位就是该数的符号位。MSB= 0表示一个正数;MSB = 1表示负数。80386 CPU具有8位(1字节)、16位(1字)和32位(双字)2的补码数据类型,分别可以表示的数据范围是:-128~127、-32768~32767、-2147483648~2146473647。另外,在80387仿真程序中使用了一种称为临时整数类型的格式,如图11-1所示。它的长度为10字节,可表示64位整型数据类型。其中低8字节最大可表示63位无符号数,而最高2字节仅使用了最高有效位来表示数值的正负。对于32位整型值则使用低4字节来表示,16位整型值则使用低2字节表示。
数的偏置表示法通常用于表示浮点数格式中的指数字段值。把一个数加上指定的偏置值就是该数的偏置数表示的值。从表11-1可以看出,这种表示方法的数值具有无符号数的大小顺序。因此这种表示方法易于比较数值大小。即大数值的偏置表示值总是无符号值的一个大数,而其他两种表示方式却并非如此。
符号数表示法有一个位专门用于表示符号(0表示正数,1表示负数),而其他位则与无符号整数表示的数值相同。浮点数的有效数(尾数)部分使用的就是这种表示方法,而符号位代表整个浮点数的正负符号。
2.BCD码数据类型
BCD(Binary Coded Decimal)码数值是二进制编码的十进制数值,对于压缩的BCD编码,每个字节可表示两位十进制数,其中每4位表示一位0~9的数。例如,十进制数59的压缩BCD码表示是0x01011001。对于非压缩的BCD码,每个字节只使用低4位表示1位十进制数。
80387协处理器支持10字节压缩BCD码的表示和运算,可表示18位十进制数,如图11-2所示。与临时整数格式类似,其中最高字节仅使用了符号位(最高有效位)来表示数值的正负,其余位均不用。若BCD码数据是负数,则会使用最高地址处1字节的最高有效位置1来表示负值。否则最高字节所有位均是0。

#p#3.浮点数据类型
具有整数部分和小数(尾数)部分的数称为实数或浮点数。实际上整型数是小数部分为0的实数,是实数集的一个子集。由于计算机使用固定长度位来表示一个数,因此并不能精确地表示所有实数。由于计算机表示实数时为了在固定长度位内能表示尽量精确的实数值,分配给表示小数部分的位个数并不是固定的,即小数点是可以“浮动”的,因此计算机表示的实数数据类型也称为浮点数。为了便于程序移植,目前计算机中都使用IEEE标准754指定的浮点数表示方式来表示实数。
这种实数表示方式的一般格式如图 11-3 所示。它由有效数(Significant)部分、指数(Exponent)部分和符号位(Sign)组成。80387协处理器支持三种实数类型,它们每个部分使用的位数如图11-4所示。

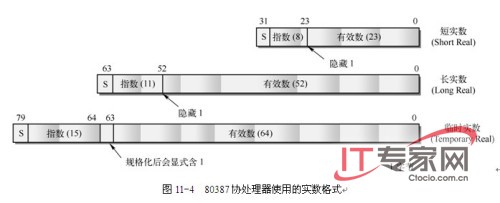
其中S是一个位的符号位。S=1表示是负实数;S=0表示是正实数。有效数(Significant)给出了实数数值的有效位数或尾数。当使用指数时,一个实数可以表示成多种形式。例如十进制数字10.34可以表示成1034.0×10-2、10.34×100、1.034×101或0.1034×102等。为了使计算能够得到最大精度值,我们总是对实数进行规格化(Normalize)处理,即调整实数的指数值,使得二进制最高有效数值总是1,并且小数点就位于其右侧。因此,上述例子正确的规格化处理结果就是1.034×101。对于二进制数来说就是1.XXXXX×2N(其中X是1或0)。如果我们总是使用这种形式来表示一个实数,那么小数点左边肯定是1。所以在80387的短实数(单精度)和长实数(双精度)格式中,这个“1”就没有必要明确地表示出来。因此在短实数或长实数的二进制有效数中,0x0111...010实际上就是0x1.0111...010。
格式中的指数字段含有把一个数表示成规格化形式时所需要的2的幂次值。正如前面提到的,为了便于数字大小的比较,80387使用偏置数形式来存储指数值。短实数、长实数和临时实数的偏置基量分别是127、1023和16383。因此一个短实数指数值0b10000000实际表示21(0b01111111 + 0b00000001)。
另外,临时实数是80387内部运算时表示数的格式。它的最高有效数1被明确地放置在位63处,并且无论你给出的数是什么数据类型的(例如,整型数、短实数或BCD码数等),80387都会把它转换成临时实数格式。80387这样做的目的是为了使得精度最大化并且尽量减少运算过程中的溢出异常。显式地把1表示出来是因为80387在运算过程中确实需要该位(用于表示极小的数值)。当输入到80387中的短型或长型实数被转换成临时实数格式时,就会明确地在位63处放置一个1。
4.特殊实数
与上面表中格式某些值无法表示的情况类似,使用实数格式表示的某些值也有其特殊含义。对于80位长度格式的临时实数,80387并没有使用其可表示的所有范围数值。表11-3是80387使用中的临时实数所能表示的所有可能的数值,其中有效数一栏虚线左侧1位表示临时实数位63,即明确表示数值1的位。短实数和长实数没有此位,因此也没有表中的伪非规格化类别。下面说明其中的一些特殊值:零值、无穷值、非规格化值、伪非规格化值以及信号NaN(Not a Number)和安静NaN。
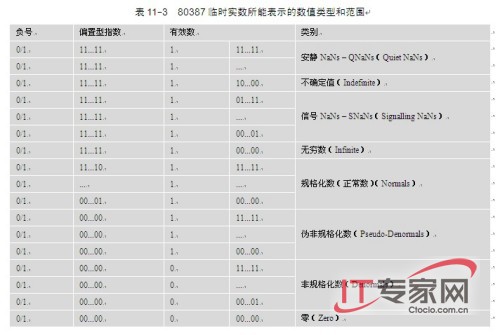
零是指数和有效数均为0的值,其余指数为0的值作保留,即指数是0的值不能表示一个正常实数值。无穷值是指数值为全1、有效数值为全零的值,而且指数值为0x11...11的所有其余值也作保留使用。
#p#非规格化数(Denormals)是一种用于表示非常小数值的特殊类值。它可以表示渐进下溢或渐进精度丢失情况。通常要求数值表示成规格化数(左移直到有效数的最高有效位是位1)。然而非规格化数的有效数最高有效位不是1。此时偏置型指数0x00...00分别是值为2-126、2-1022、2-16382的短实数、长实数和临时实数指数值的特殊表示方式。这种表示比较特殊,因为偏置型指数0x00...01对三种实数类型也分别表示相同的指数值2-126、2-1022、2-16382。
伪非规格化类数值(Pseudo-denormals)是有效数最高有效位为1的值,而非规格化类数值的该位是0。伪非规格化数很少见,它们可以用规格化类数来表示却没有这么做。因为上面已经说明特殊的偏置指数0x00...00与规格化数的指数0x00...01具有相同的值。因此伪非规格化类数可以表示成规格化类数值。
另一种特殊情况是NaN。NaN是指“不是一个数”(Not a Number)。NaN有两种形式:会产生信号(Signaling)的和不会产生信号的或称为安静的(Quiet)。当一个产生信号的NaN(SNaN)被用于操作时就会引发一个无效操作异常,而一个安静的NaN(QNaN)则不会。SnaN是一类会引发无效操作异常的数值。使用的方法就是程序先把变量都初始化为SNaN值,在实际使用这个变量时还需要对其进行真正的赋值。这样若操作过程中使用了一个未被初始化的值就会引发异常。当然,NaN类数值也可以用来存储其他信息。
80387自身不会产生SNaN类的值,但会产生QNaN类的值。当发生无效操作异常时80387就会产生一个QNaN类值,并且操作的结果将是不确定值(Indefinite)。不确定值是一种特殊的QNaN类值。每种数据类型都有一个表示不确定值的数。对于整型数则是用其最大负数来表示其不确定值。
另外还有一些80387不支持的临时实数值,即那些没有在上表中列出的数值范围。若80387遇到这些数值,就会引发无效操作异常。
11.1.2 数学协处理器功能和结构
80386虽然是一个通用微处理器,但其指令并不是非常适用于数学计算。因此若使用80386来执行数学计算,那么就需要编制非常复杂的程序,而且执行效率也相对较低。80387作为80386的辅助处理芯片,极大地扩展了程序员的编程范围。以前程序员不太可能做到的事,使用协处理器后就可以很容易地,并且快速而精确地完成。
80387具有一组特别的寄存器。这组寄存器可以让80387直接操作比80386所能处理的大或小几个数量级的数值。80386使用2进制补数方式表示一个数。这种方法不适合用来表示小数。而80387并不使用2的补数方法来表示数值,它使用了IEEE标准754规定的80位(10个字节)格式。这种格式不仅具有广泛的兼容性,而且能够使用二进制表示极大(或极小)的数值。例如,它能表示大到1.21×104932数值,也能处理小到3.3×10-4932的数。80387并不保持固定小数点的位置,如果数值小的话就多使用一些小数位,如果数值大的话就少用几位小数位。因此小数点的位置是可以“浮动”的。这也是术语“浮点”数的由来。
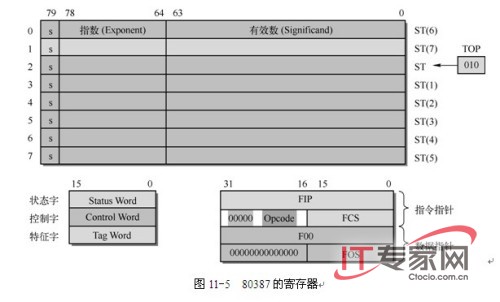
为支持浮点运算,80387中包含三组寄存器,如图11-5所示。① 8个80位长的数据寄存器(累加器),可用于临时存放8个浮点操作数,并且这些累加器可以执行栈式操作;② 3个16位状态和控制寄存器:一个状态字寄存器SWD、一个控制字寄存器CWD和一个特征(TAG)寄存器;③ 4个32位出错指针寄存器(FIP、FCS、FOO和FOS)用于确定导致80387内部异常的指令和内存操作数。
#p#
1.栈式浮点累加器
在浮点指令执行过程中,8个80位长度的物理寄存器组被作为栈式累加器使用。虽然每个80位寄存器有固定的物理顺序位置(即左边的0~7),但当前栈顶则由ST(即ST(0))来指明。ST之下的其余累加器使用名称ST(i)来指明(i = 1~7)。至于哪个80位物理寄存器是当前栈顶ST,则由具体操作过程指定。在状态字寄存器中名称为TOP的3位字段含有当前栈顶ST对应的80位物理寄存器的绝对位置。一个入栈(Push)操作将会把TOP字段值递减1,并把新值存储于新的ST中。在入栈操作之后,原来的ST变成了ST(1),而原来的ST(7)变成了现在的ST。即所有累加器的名称都从原来的ST(i)变成了ST((i+1)&0x7)。一个出栈(Pop)操作将会读出当前ST对应的80位寄存器的值,并且把TOP字段值递增1。因此在出栈操作之后,原来的ST(即ST(0))变成了ST(7),原来的ST(1)成为新的ST。即所有累加器的名称都从原来的ST(i)变成ST((i-1)& 0x7)。
ST的作用如同一个累加器是因为它被作为所有浮点指令的一个隐含操作数。若有另一个操作数,那么该第2个操作数可以是任何其余累加器之一ST(i),或者是一个内存操作数。栈中的每个累加器为一个实数提供了使用临时实数格式存储的80位空间,其最高位(s)是符号位,位78~64是15位的指数字段,位63~0是64位的有效数字段。
浮点指令被设计成能充分利用这个累加器栈模式。浮点加载指令(FLD等)会从内存中读取一个操作数并压入栈中,而浮点存储指令则会从当前栈顶取得一个值并写到内存中。若栈中该值不再需要时还可以同时执行出栈操作。加和乘之类的操作会把当前ST寄存器内容作为一个操作数,而另一个取自其他寄存器或内存中,并且在计算完后即把结果保存在ST中。还有一类“操作并弹出”操作形式用于在ST和ST(1)两者之间进行运算。这种操作形式会执行一次弹出操作,然后把结果放入新的ST中。
2.状态与控制寄存器
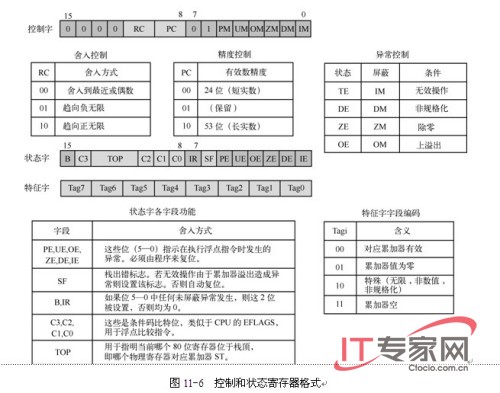
三个16位的寄存器(TAG字、控制字和状态字)控制着浮点指令的操作并且为其提供状态信息。它们的具体格式如图11-6所示。下面逐一对它们进行说明。
(1)控制字
控制字(Control Word)可用于程序设置各种处理选项来控制80387的操作。其中可分为三个部分。位11~10的RC(Rounding Control)是舍入控制字段,用于对计算结果进行舍入操作。位9~8的PC(Precision Control)是精度控制字段,用于在保存到指定存储单元之前对计算结果进行精度调整。所有其他操作使用临时实数格式精度,或者使用指令指定的精度。位5~0是异常屏蔽位,用于控制协处理器异常处理。这6位对应80387可能发生的6种异常情况。其中每一种异常都可以单独屏蔽掉。如果发生某个特定异常并且其对应屏蔽位没有置位,那么80387就会向CPU通报这个异常,并且会让CPU产生异常中断int 16。然而如果设置了对应屏蔽位,那么80387就会自己处理并纠正发生的异常问题而不会通知CPU。这个寄存器随时可以读写,其中各位的具体含义参见图11-6。
(2)状态字
在运行期间,80387会设置状态字(Status Word)中的位,用于程序检测特定的条件。当发生异常时,它可让CPU确定发生异常的原因。因为所有6个协处理器异常都会让CPU产生异常中断int16。
(3)特征字
特征字(Tag Word)寄存器含有8个2位的Tag字段,分别对应8个物理浮点数据寄存器。这些特征字段分别指明相应的物理寄存器含有有效、零、特殊浮点数值,或者是空的。特殊数值是指那些无限值、非数值、非规格化或不支持格式的数值。特征字段Tag可用于检测累加器堆栈上下溢出情况。如果入栈(Push)操作递减TOP指向了一个非空寄存器,就会发生栈上溢出。如果出栈(Pop)操作企图去读取或弹出空寄存器,就会造成栈下溢出(Underflow)。栈的上下溢出都将引发无效操作异常。
#p#3.出错指针寄存器
出错指针寄存器(Error-Pointer Register)是4个32位的80387寄存器,其中含有80387最后执行指令和所用数据的指针,参见图11-6。前两个寄存器FIP和FCS中是最后执行指令中2个操作码的指针(忽略前缀码)。FCS是段选择符和操作码,FIP是段内偏移值。后两个寄存器FOO和FOS是最后执行指令内存操作数的指针。FOS中是段选择符,FOO中是段内偏移值。如果最后执行的协处理器指令不含内存操作数,则后两个寄存器值无用。指令FLDENV、FSTENV、FNSTENV、FRSTOR、FSAVE和FNSAVE用于加载和保存这4个寄存器的内容。前3条指令共加载或保存28字节内容:控制字、状态字和特征字以及4个出错指针寄存器。控制字、状态字和特征字都以32位操作,高16位为0。后3条指令用于加载或保存协处理器所有108字节的寄存器内容。
4.浮点指令格式
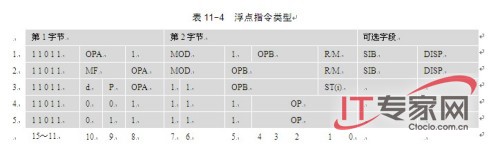
对协处理器进行仿真就是解析具体的浮点指令操作码和操作数,根据每一条指令的结构使用80386的普通指令来执行相应的仿真操作。数学协处理器80387共有七十多条指令,共分5类,见表11-4。每条指令的操作码都有2个字节,其中第一个字节高5位都是二进制11011。这5位的数值(0x1b或十进制27)正好是字符ESC(转义)的ASCII代码值,因此所有数学协处理器指令都被形象地称为ESC转义指令。在仿真浮点指令时可忽略相同的ESC位,只要判断低11位的值即可。
表中各个字段的含义如下(有关这些字段的具体含义和详细说明请参考80x86处理器手册):
1)OP(Operation opcode)是指令操作码,在有些指令中它被分成了OPA和OPB两部分。
2)MF(Memory Format)是内存格式。00:32位实数;01:32位整数;10:64位实数;11:64位整数。
3)P(Pop)指明在操作后是否要执行一次出栈处理。0:不需要;1:操作后弹出栈。
4)d(destination)指明保存操作结果的累加器。0:ST(0);1:ST(i)。
5)MOD(Mode)和R/M(Register/Memory)是操作方式字段和操作数位置字段。
6)SIB(Scale Index Base)和DISP(Displacement)是具有MOD和R/M字段指令的可选后续字段。
另外,所有浮点指令的汇编语言助记符都以字母F开头,例如:FADD、FLD等。还有如下一些标准表示方法:
1)FI 所有操作整型数据的指令都以FI开头,例如FIADD、FILD等。
2)FB 所有操作BCD类型数据的指令都以FB开头,例如FBLD、FBST等。
3)FxxP 所有会执行一次出栈操作的指令均以字母P结尾,例如FSTP、FADDP等。
4)FxxPP 所有会执行二次出栈操作的指令均以字母PP结尾,例如FCOMPP、FUCOMPP等。
5)FNxx 除了以FN开头的指令,所有指令在执行前都会先检测未屏蔽的运算异常。而以FN开头的指令不检测运算异常情况,例如FNINIT、FNSAVE等。

























