C#实例讲解二叉树原理与实现-c# 二叉树

按：这是以前遇到的一个微软技术面试题，当时觉得比较麻烦，要涉及到使用树 tree 等数据结构，所以一直保留在脑海中。今天下午碰巧拿到了传说中的 Dragon Book，于是尝试自己动手写写看。

花了2个小时写的这个解释器还是比较简单的，仅仅能够做四则运算。现在还不支持括号，以及一元运算符，比如负号运算符。源代码可以在这里下载：http://files.cnblogs.com/yinyueyouge/Arithemic.7z

运行的主界面如下：

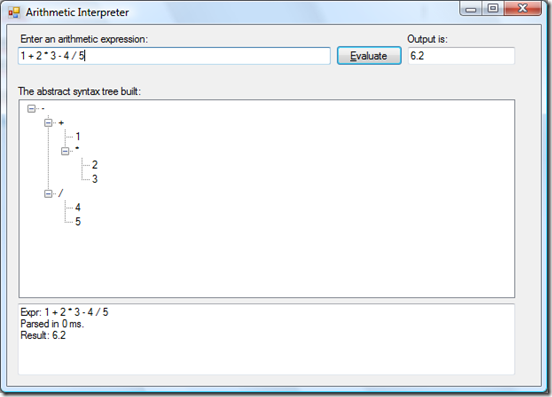
解释器也能够判断非法的输入：

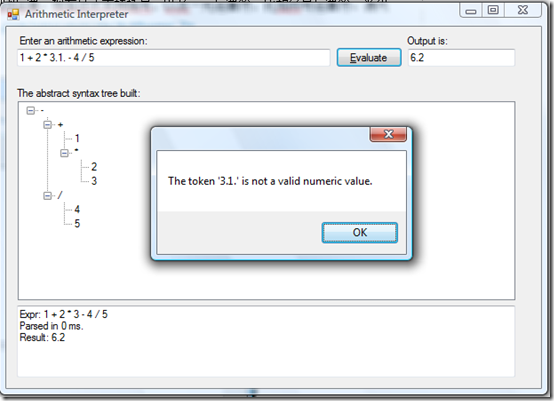
现在这个解释器还非常原始。若是有 bug 发现，请提示出来，我会更正。：）

现在来解说下这个解释器的原理。

一、输入和输出

输入是一个用字符串表达的四则运算，比如 1 + 2 * 3 。目的是试图去理解这个字符串表达的运算指令，然后计算出结果 7。之所以是一个解释器 Interpreter，而不是一个编译器 Compiler，是因为程序是去理解指令并且执行指令，而不是把指令编译成机器代码来运行；后者是编译器的目标。

在解释的过程中，要能够分辨出不合法的指令：比如非法的字符 abc，非法的数字 2.3.1.4，非法的运算指令 2 * + 3，还有等等。

整个程序可以分为两个部分：

第一个部分，是截取输入字符串，然后返回单元指令。比如，对于指令 1 + 2 * 3 – 4 / 5，就需要被分解成如下所示的单元指令集：

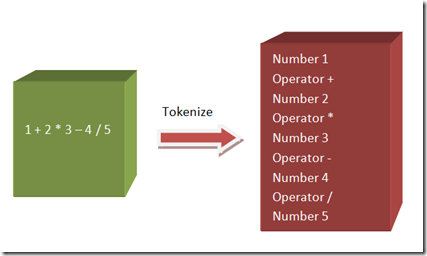
第二个部分，是把单元指令集（上图橙色包含部分）组成一个树结构，称之为 Abstract Syntax Tree。按照将来需要解释的顺序，优先执行的指令会放在树的叶的位置，最后执行的指令会是树的根 Root。

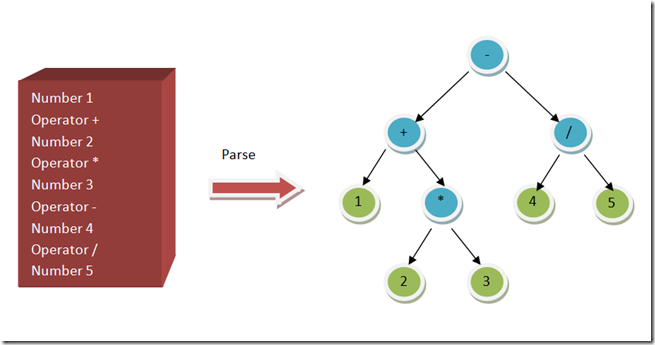
在上图所示的 Abstract Syntax Tree 中，最先执行的指令是位于树上最深的子树，也就是 * ，然后是第二级的 + 和 / ，最后执行的位于根的指令 – 。

二、截取单元指令 (Tokenize)

因为程序比较简单，只有 2 种单元指令：NumToken 和 OpToken。

我定义了一个基本类，叫做 Token，然后 NumToken 和 OpToken 继承了该基本类。

Class Token：什么也没有，暂时是空壳子。

internal abstract class Token
{
}

Class NumToken: 表述一个数。

internal sealed class NumToken : Token
{
    public double Value { get; }
}

Class OpToken: 表述一个运算符。

internal sealed class OpToken : Token
{
    public Op Value { get; }
    public Prioirty Prioirty { get; }
}

Op 和 Priority 是 2 个 enum:

internal enum Op : int
{
    Plus = '+',
    Minus = '-',
    Multiply = '*',
    Divide = '/'
}
internal enum Prioirty
{
    Lv2 = 2,
    Lv1 = 1,
    Lv0 = 0
}

截取的算法相对来说很简单，是由 Tokenizer 类来实现的。这个类是 internal sealed，因为外界不需要知道它的存在。Tokenizer 会被 Intepreter 类所使用。

internal sealed class Tokenizer
{
    public Token[] Parse(string value);
}

在 Parse 函数里面，扫描输入字符串，从第一个字符开始，一直到最后一个字符。空白字符会被忽略掉。

我们定义了个缓冲 buffer，用来存储已经扫描到的数字。若是遇到了一个非数字，就把缓冲区所有的存储的字节转变成 double 类型，然后保存下来。值得注意的是，对小数点的处理。若是缓冲区里面已经存在了一个小数点，遇到一个新的小数点就应该抛出错误。

每当扫描到一个操作符，比如 +, –, *, /，就把他们当作一个操作符存储起来。这里要注意的是，数字的正负号其实是一个一元操作符，是何数字分开保存的。

遇到其他没有定义的字符，就直接抛出错误。

三、创建 Abstract Syntax Tree

这里需要考虑到2个不同的正常情况：

1、不同级别的操作符：+和-的优先等级比较低，×和/的优先等级比较高

2、同级别的操作符，操作的顺序。比如，+和-的优先顺序是从左往右。

从最简单的情况开始考虑：分析 1 + 2 + 3 + 4

首先，AST 树是空的， Root = NULL。

当把 NumToken 1 插入树的时候，简单的设置该 Token 为根即可。

当把 OpToken + 插入树的时候，我们就需要挪动树，把 + 设置成根：

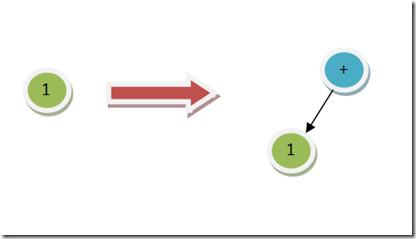
当把 NumToken 2 插入树的时候，我们就把数字 2 插入树的右侧：

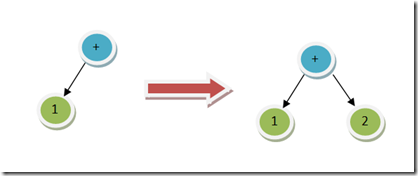
当把 OpToken + 插入树的时候（同级别的操作符，顺序是左到右），我们就需要把最新的 OpToken 设置成根，当前树设置成新根的左侧：

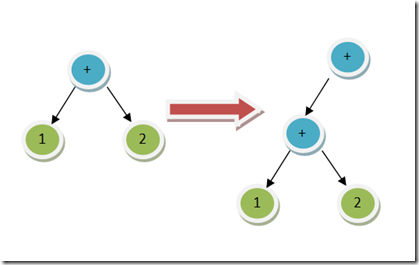
到这里为止，我们可以得出一个很重要的法则：插入一个新的操作符进入 AST 树的时候，若是树的根是一个操作符，并且和此新操作符同级，运算顺序是由左至右的话，那么新的操作符会成为新的树的根，现有的树会成为新树的左子树。

实际上，整个解释器的开发，遵从“启发式 heuristic ”的原理。整个解释的过程可以分解成一条条的“规则”，我们需要做的是把规则全部“找”出来，并且把规则制定的尽可能完善。

好了，回到刚才的分析上。假设要插入的操作符不是 +，而是一个优先权比较高的 * 呢？也就是，若是 1 + 2 * 3 的话，AST 会是什么样子？

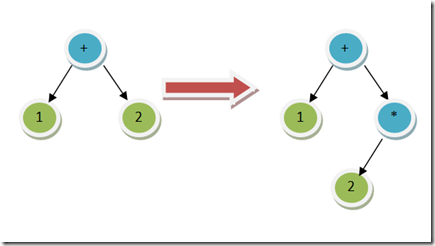
这种情况下，乘法运算符必须移动到树的右子树上，并且成为右子树的根。原右子树会成为新的右子树的左子树。

插入操作符的代码实现如下：

if (token is OpToken) {
    if (root.Token is OpToken && root.RightChild == null) {
        throw new ParseFailureException(
            "The expression '{0} {1}' is not a valid arithmetic expression.",
            root.Token.ToString(),
            token.ToString()
        );
    }
    if (root.Token is NumToken) {
        Syntax newRoot = new Syntax(token);
        newRoot.LeftChild = root;
        root = newRoot;
        return newRoot;
    }
    if (root.Token is OpToken) {
        // Compare prioirty of the two operators
        OpToken token1 = (OpToken)token;
        OpToken token2 = (OpToken)root.Token;
        if (token1.Prioirty <= token2.Prioirty) {
            Syntax newRoot = new Syntax(token1);
            newRoot.LeftChild = root;
            root = newRoot;
            return newRoot;
        }
        if (token1.Prioirty > token2.Prioirty) {
            root.RightChild = Append(root.RightChild, token);
            return root;
        }
    }

插入数字 NumToken 怎么处理呢？这个很简单，NumToken总是成为右子树。代码如下（这里用到了线性递归，可以换成用尾端递归来提高效率）：

if (token is NumToken) {
    if (root.Token is OpToken) {
        if (root.RightChild == null) {
            Syntax newNode = new Syntax(token);
            root.RightChild = newNode;
            return root;
        } else {
            root.RightChild = this.Append(root.RightChild, token);
            return root;
        }
    } else {
        throw new ParseFailureException(
            "The expression '{0} {1}' is not a valid arithmetic expression.",
            root.Token.ToString(),
            token.ToString()
        );
    }
}

四、求运算结果

当 AST 树创建出来后，求运算结果就很简单了，用线性递归即可。

求值（根）

若是遇到 NumToken，返回值

若是遇到 OpToken +，返回求值（左子树） +　求值（右子树）

若是遇到 OpToken －，返回求值（左子树） -　求值（右子树）

….

代码如下：

private double Eval(Syntax root) {
    if (root == null) {
        return 0;
    } 
    
    if (root.Token is NumToken) {
        NumToken token1 = (NumToken)root.Token;
        return token1.Value;
    }
    if (root.Token is OpToken) {
        OpToken token1 = (OpToken)root.Token;
        if (root.RightChild == null && root.LeftChild == null) {
            throw new ParseFailureException(
                "The expression '{0}' cannot be a value.",
                root.Token.ToString()
            );
        } else {
            double lvalue = this.Eval(root.LeftChild);
            double rvalue = this.Eval(root.RightChild);
            switch (token1.Value) {
                case Op.Plus:
                    return lvalue + rvalue;
                case Op.Minus:
                    return lvalue - rvalue;
                case Op.Multiply:
                    return lvalue * rvalue;
                case Op.Divide:
                    return lvalue / rvalue;
                default:
                    throw new ParseFailureException(
                        "The expression '{0} {1} {2}' cannot be a value.",
                        root.LeftChild.ToString(),
                        root.Token.ToString(),
                        root.RightChild.ToString()
                    );
            }
        }
    }
    throw new ParseFailureException("Unrecognized token: " + 
              root.Token.ToString());
}

后记：

这个解释器还很原始。需要添加的功能有：

1、支持一元操作符 - 和 +，它们将具有最高优先权

2、支持括号。

3、支持变量，也即需要一个 Local Variable Table。。。

【编辑推荐】