深入剖析时序Prophet模型：工作原理与源码解析

随着得物业务的快速发展，积累了大量的时序数据，这些数据对精细化运营，提升效率、降低成本有着重要作用。在得物的时序数据挖掘场景中，时序预测Prophet模型使用频繁，本文对Prophet的原理和源码进行深入分析，欢迎阅读和交流。

一、引入

时间序列是指按照时间先后顺序收集或观测的一系列数据点，这类数据通常都具有一定时间相关性，基于这种顺序性，我们可以对时间序列进行多种数据挖掘任务，包括分类、聚类、异常检测和预测等。

时序任务在许多领域都有广泛的应用，包括金融、商业、医疗、气象、工业生产等。在得物的业务场景中，应用最为广泛的是时序预测问题，本文介绍的内容主要和时序预测相关。

时序预测利用历史时间序列数据构建数学统计、机器学习或深度学习等模型，来预测未来的观测值，其目的是为了对时间序列的趋势、周期性、季节性、特殊事件等规律进行捕捉并预测，从而指导业务人员做出商业、运营决策。以下是时间序列预测在得物各业务域的需求情况，总之哪里有指标，哪里就有预测。

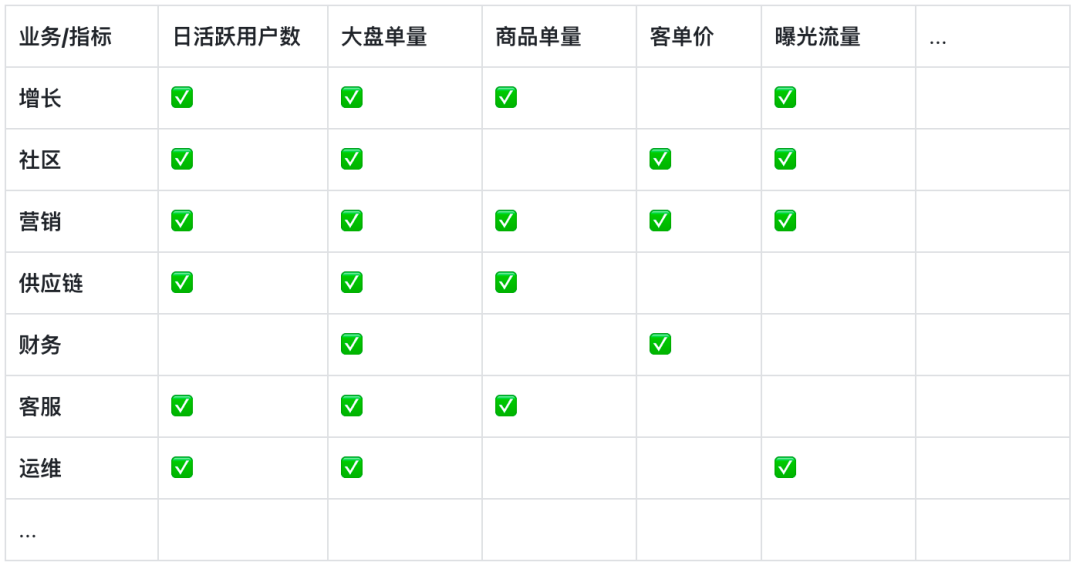
解决时序预测问题的算法研究历史非常悠久，是备受关注和持续发展的领域。根据算法原理和方法进行分类，时序预测模型可以分为以Holt-winters，ARIMA为代表的经典统计模型，用单一时序变量进行参数拟合；以线性回归、树回归为代表的传统机器学习算法，在有监督学习的框架下，构建特征来预测目标值；以及运用CNN、RNN、Transform等特征提取器，在Encoder-Decoder框架下进行预测的深度学习方法。

本文将介绍的Prophet模型和上述三种分类算法有所差异，但方法和原理上也结合了参数拟合、机器学习的思想，它将时序分解成趋势变化、季节性、节假日、外部回归因子之和，是结合时序分解的加法模型预测算法。

Prophet于2017年由Facebook’s Core Data Science team开源发布，尽管从时间上来看不是很新的模型，但是在得物实际的时序预测场景中取得了不俗的效果。目前网上的博客主要介绍了模型的基本原理、使用方式，在使用过程中笔者仍有一些疑问，例如：

• Prophet模型是如何进行训练和预测？
• 模型如何进行概率预测，得到预测的上界和下界？

笔者带着这些问题阅读了Prophet的源码，发现了一些论文中没有提到的细节和流程，对以上问题有了答案，这里分享给大家。代码参考Prophet python语言实现版本v1.1.5。

二、准备知识

如果读者有机器学习基础，熟悉最优化计算方法、贝叶斯估计、MCMC采样可以跳过这一小节，不熟悉的读者可以按照这一小节提到的概念搜索相关资料。

参数估计

通俗的说预测就是利用已知数据来推测产生该数据的模型和参数，然后用推测的模型和参数产生下一个结果。对于模型的参数估计方法，有频率学派和贝叶斯学派之分。频率学派认为模型参数是个固定的值。而贝叶斯学派是认为模型参数不是一个固定的值，而是源自某种潜在分布，希望从数据中推知该分布。

用大家最熟悉的线性回归为例，假设噪声服从正态分布：

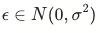
在概率视角下，线性回归可以表示为：

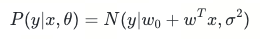
其中θ=(w0,w,σ^2)是模型所有的参数。

在频率学派视角下θ是一个常量，可以用极大似然估计来估计参数值。其思想是对于N个观测样本来说使得其发生概率最大的参数就是最好的参数。整个观测集发生的概率为：

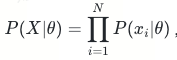
由于连乘不容易参数求解，可以采用最大对数似然方法，线性回归有解析解，我们可以直接求导计算得到最优的θ_hat：

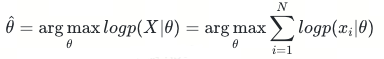
在贝叶斯学派视角下θ是一个随机变量而不是一个固定的值，由一个先验分布进行约束，通过利用已知样本进行统计推断。贝叶斯学派认为一个好的θ不仅要考虑似然函数P(X|θ)还要考虑θ的先验分布P(θ)，即最大化P(X|θ)P(θ)。由于X的先验分布是固定的常数，最大化函数可以写成P(X|θ)P(θ)/P(X)，根据贝叶斯公式可知P(X|θ)P(θ)/P(X)=P(θ|X)，即找到一个θ_hat能够最大化后验概率P(θ|X)。

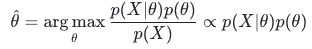
求解参数θ可以选择使用最大后验估计（Maximum A Posterior, MAP）或者贝叶斯估计两种方法，最大后验估计直接求解让后验概率最大的θ。这样问题就转化还成一个约束问题，实际中可以使用梯度下降、牛顿法或者L-BFGS拟牛顿法等数值优化方法进行求解。

从最大似然估计和最大后验估计来看求解的参数θ是一个确定值，但贝叶斯估计不是直接估计θ，而是估计θ的分布。在最大后验估计中由于求θ极值过程中与P(X)无关，分母可以被忽略。但是在贝叶斯估计中是求整个后验概率的分布，分母不能忽略。对于连续型随机变量有：

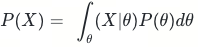
则贝叶斯公式变为：

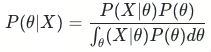
分母是积分形式一般没有解析解，直接计算是非常困难的。于是引入马尔可夫链蒙特卡洛算法（Markov Chain Monte Carlo, MCMC）进行采样，从而得到各个参数的一系列采样值。

Stan开源框架

https://mc-stan.org/ : Stan is a state-of-the-art platform for statistical modeling and high-performance statistical computation.

Stan是一个用于贝叶斯统计建模和推断的开源框架，包含了定义概率模型的编程语言，以及高效执行贝叶斯推断的算法库，被广泛用于统计建模和机器学习任务，它集成了上文谈到的MAP、MCMC等求解算法，在Python中可以通过PyStan包来使用 Stan。

Prophet基本原理

Prophet基于时间序列分解和参数拟合来实现高效的训练和预测。首先Prophet定义了一个关于时间步t的加法函数，函数值由趋势项、季节项、节假日项、外部因子项以及观测噪声组成，核心公式如下：

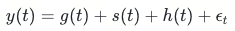
其中g(t)代表趋势项，s(t)代表季节项，h(t)代表节假日项（泛指外部回归变量），ε_t代表误差项。具体各项公式可以参考附录中的文章以及官方论文。其中季节项、节假日项、外部因子项可以统一视为回归因子，除了构造特征的方法不同以外，在模型训练和预测阶段都是一样的处理方法。

Prophet其实是一种广义线性模型，其数学形式是：

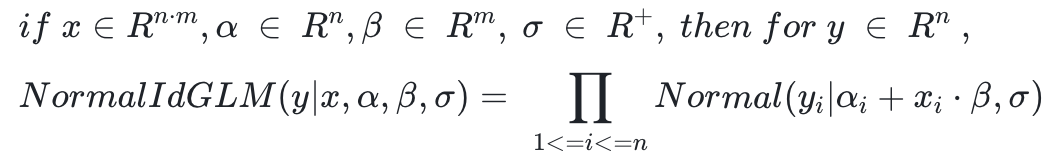
其中y是历史label数据，x是Prophet中的加法回归因子变量，α是趋势项*（1+乘法回归因子变量），β是回归因子的权重，σ是噪声服从高斯分布。模型训练的就是公式中未知参数，Prophet的python代码负责数据输入、预处理、流程控制、可视化等部分功能，核心算法求解模块调用Stan进行求解。Stan有自己定义的一套语言体系，定义了变量、输入数据和模型，Prophet数学模型转化成Stan的建模语言如下表示：

• 变量和数据

data {
  int T;                // Number of time periods
  int<lower=1> K;       // Number of regressors
  vector[T] t;          // Time
  vector[T] cap;        // Capacities for logistic trend
  vector[T] y;          // Time series
  int S;                // Number of changepoints
  vector[S] t_change;   // Times of trend changepoints
  matrix[T,K] X;        // Regressors
  vector[K] sigmas;     // Scale on seasonality prior
  real<lower=0> tau;    // Scale on changepoints prior
  int trend_indicator;  // 0 for linear, 1 for logistic, 2 for flat
  vector[K] s_a;        // Indicator of additive features
  vector[K] s_m;        // Indicator of multiplicative features
}

• 模型

model {
  //priors
  k ~ normal(0, 5);
  m ~ normal(0, 5);
  delta ~ double_exponential(0, tau);
  sigma_obs ~ normal(0, 0.5);
  beta ~ normal(0, sigmas);


  // Likelihood
  y ~ normal_id_glm(
    X_sa,
    trend .* (1 + X_sm * beta),
    beta,
    sigma_obs
  );
}

论文中各项成分的参数预先设定了先验分布，根据：

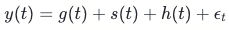
能够得到后验概率，根据第二部分提到的参数估计方法，运用最大后验估计或MCMC采样即可得到参数估计值。

三、Prophet源码剖析

代码结构

Prophet代码目录如下所示，核心逻辑主要是Prophet.stan、models.py、forecaster.py三个脚本，本文的分享主要围绕这三个脚本。

|-- stan
    |-- Prophet.stan # stan语言实现的Prophet模型
|-- setup.py
|-- Prophet
    |-- serialize.py # Prophet训练完成的模型的序列化、模型的存储和加载，以便后续重用。
    |-- plot.py # 可视化模块
    |-- models.py # stan模型定义
    |-- diagnostics.py # 用于诊断 Prophet 模型性能的函数，比如计算误差指标、绘制诊断图等。
    |-- tests # 封装的测试脚本
    |-- __init__.py
    |-- __version__.py
    |-- forecaster.py #  Prophet 类的定义，模型的核心逻辑，数据的处理、模型的拟合和预测等功能
    |-- utilities.py # 包含了一些辅助函数，用于处理时间序列数据、特征工程等。
    |-- make_holidays.py # 节假日具体日期的构造

• Prophet.stan：用Stan编程语言实现的Prophet模型脚本。
• models.py：python和Stan语言交互的模块，定义使用Stan脚本语言时的输入数据，拟合参数、输出数据，控制Stan进行参数拟合、采样。
• forecaster.py：Prophet模型核心代码，定义了Prophet类，涉及整个模型的数据处理、模型训练和模型推理等功能。

模型框架

Prophet模型训练-预测流程如下所示：

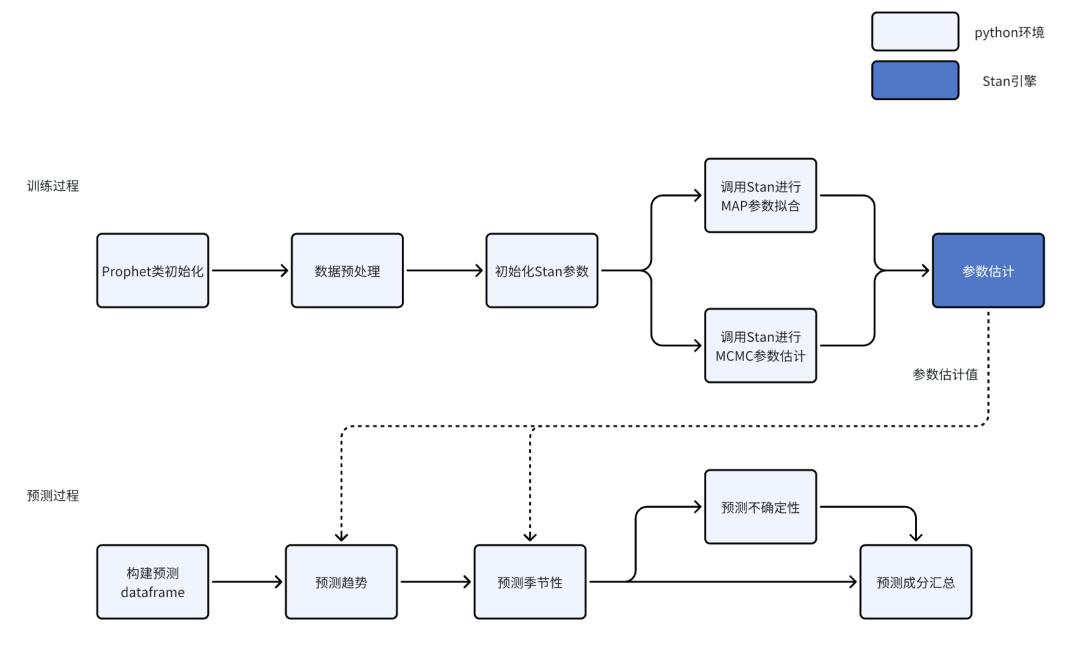
初始参数

• Prophet类初始化
  初始化模块主要是读取预先设定和Prophet有关的模型参数。分别有以下几类：

趋势项相关

growth: String 'linear', 'logistic' or 'flat' to specify a linear, logistic or
    flat trend.
changepoints: List of dates at which to include potential changepoints. If
    not specified, potential changepoints are selected automatically.
n_changepoints: Number of potential changepoints to include. Not used
    if input `changepoints` is supplied. If `changepoints` is not supplied,
    then n_changepoints potential changepoints are selected uniformly from
    the first `changepoint_range` proportion of the history.
changepoint_range: Proportion of history in which trend changepoints will
    be estimated. Defaults to 0.8 for the first 80%. Not used if
    `changepoints` is specified.
changepoint_prior_scale: Parameter modulating the flexibility of the
    automatic changepoint selection. Large values will allow many
    changepoints, small values will allow few changepoints.

• 季节性相关

yearly_seasonality: Fit yearly seasonality.
    Can be 'auto', True, False, or a number of Fourier terms to generate.
weekly_seasonality: Fit weekly seasonality.
    Can be 'auto', True, False, or a number of Fourier terms to generate.
daily_seasonality: Fit daily seasonality.
    Can be 'auto', True, False, or a number of Fourier terms to generate.
holidays: pd.DataFrame with columns holiday (string) and ds (date type)
    and optionally columns lower_window and upper_window which specify a
    range of days around the date to be included as holidays.
    lower_window=-2 will include 2 days prior to the date as holidays. Also
    optionally can have a column prior_scale specifying the prior scale for
    that holiday.
seasonality_mode: 'additive' (default) or 'multiplicative'.
seasonality_prior_scale: Parameter modulating the strength of the
    seasonality model. Larger values allow the model to fit larger seasonal
    fluctuations, smaller values dampen the seasonality. Can be specified
    for individual seasonalities using add_seasonality.
holidays_prior_scale: Parameter modulating the strength of the holiday
    components model, unless overridden in the holidays input.
holidays_mode: 'additive' or 'multiplicative'. Defaults to seasonality_mode.

• 参数拟合相关

growth: String 'linear', 'logistic' or 'flat' to specify a linear, logistic or
    flat trend.
changepoints: List of dates at which to include potential changepoints. If
    not specified, potential changepoints are selected automatically.
n_changepoints: Number of potential changepoints to include. Not used
    if input `changepoints` is supplied. If `changepoints` is not supplied,
    then n_changepoints potential changepoints are selected uniformly from
    the first `changepoint_range` proportion of the history.
changepoint_range: Proportion of history in which trend changepoints will
    be estimated. Defaults to 0.8 for the first 80%. Not used if
    `changepoints` is specified.

• 不确定性相关

mcmc_samples: Integer, if greater than 0, will do full Bayesian inference
    with the specified number of MCMC samples. If 0, will do MAP
    estimation.
interval_width: Float, width of the uncertainty intervals provided
    for the forecast. If mcmc_samples=0, this will be only the uncertainty
    in the trend using the MAP estimate of the extrapolated generative
    model. If mcmc.samples>0, this will be integrated over all model
    parameters, which will include uncertainty in seasonality.
uncertainty_samples: Number of simulated draws used to estimate
    uncertainty intervals. Settings this value to 0 or False will disable
    uncertainty estimation and speed up the calculation.
stan_backend: str as defined in StanBackendEnum default: None - will try to

训练过程

数据预处理

• 数据检查

python.Prophet.forecaster.Prophet.setup_dataframe

Prophet会检查模型输入参数、数据的合法性，帮助使用者快速定位问题。比如：

检查输入数据中是否有y列，ds列是否符合时间输入规范，是否有缺失值。

检查添加的额外回归项，是否有缺失值，是否输入数据中有添加的回归项数据。

季节性项的condition列值是否是bool值等，用于控制模型选择性的学习condition为True的样本。

• 数据归一化

python.Prophet.forecaster.Prophet.initialize_scales

对于y，有Absmax和Minmax两种方式：现实场景中特征值或y，往往有很大的量纲差异，会降低模型的性能、预测的准确性。Prophet内置了对y和对外部回归因子add regressors的归一化。

AbsMax归一化：
含义：AbsMax归一化是将原始数据缩放到[-1, 1]的范围内，使数据的绝对值最大值为1。
适用场景：AbsMax归一化适用于数据中存在明显的异常值或极端值的情况，可以保留数据的分布形状并减少异常值对模型的影响。

MinMax归一化：
含义：MinMax归一化是将原始数据缩放到[0, 1]的范围内，使数据的最小值对应0，最大值对应1。
适用场景：MinMax归一化适用于需要将数据映射到一个固定范围内的情况，保留了原始数据的相对关系，在大部分机器学习算法中经常用到。

if self.scaling == "absmax":
    self.y_min = 0.
    self.y_scale = float((df['y']).abs().max())
elif self.scaling == "minmax":
    self.y_min = df['y'].min()
    self.y_scale =  float(df['y'].max() - self.y_min)
    ...
    ...

对于add regressor特征则进行标准化，将特征数据缩放到均值为0，标准差为1的标准正态分布。

python/Prophet/forecaster.py:389

计算得到的y_scale和回归项的均值和标准差，会更新到Prophet类中，供预测阶段使用。

自动设置周期性

python.Prophet.forecaster.Prophet.set_auto_seasonalities

如果在初始化Prophet类时，没有指定季节性相关的参数，则会根据数据长度和间隔自动增加季节性项，三种不同的周期性默认的傅立叶阶数为10。

当历史数据大于等于两年，则增加yearly seasonality，默认周期为365.25；
当历史数据大于等于两周，且相邻两数据之间的时间之差小于1周，则打开weekly seasonality，默认周期为7；
当历史数据大于等于2天，且相邻两数据之间的时间小于1天，则打开daily seasonality，默认周期为1；

生成特征宽表

Prophet模型的成分中划分了seasonality features、holiday features和add regressors，但其实是一样的处理方法。根据Prophet类初始化时的参数，生成特征宽表，行为依次递增的时间序列，列为每一个feature对应的值。

对于某一个seasonality特征，根据传入的周期性和傅立叶阶数，生成不同列，列数等于傅立叶阶数，列值等于某一阶的周期性函数值。然后结合该特征对应的condition_name的值，得到最终的特征值。condition_name是True、False的np.array类型，用来指导模型学习condition_name列中为True的时间段数据，忽略为False的时间段的数据。

对于holiday features和add regressors，则对于每一个特征，生成一列，列为每一个feature对应的值。特征宽表的特征总数为seasonality特征的傅立叶阶数+holiday features数+add regressors数。

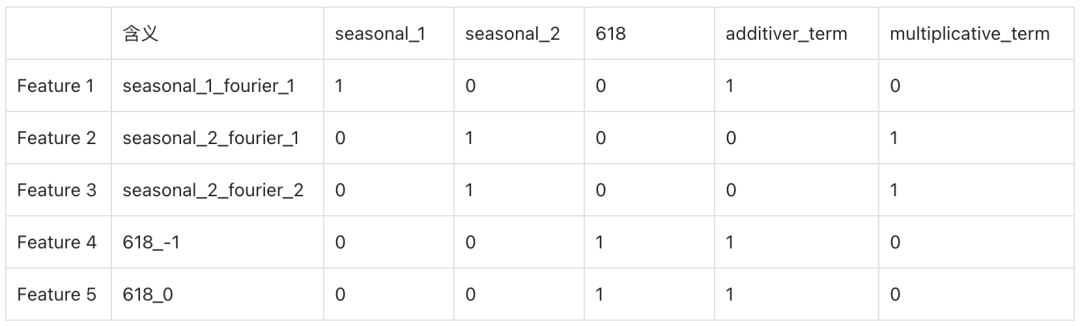
在生成特征宽表的同时，Prophet会定义component_cols变量，来维护哪些列同属于同一个成分。比如把同一个季节性项的多个周期函数合并成一个成分，把同一个节假日不同时间的因子合并成一个成分，把加性或者乘性因子项合并成一个成分，这样可以方便进行模型的成分分析和结果可视化。比如给定一个Prophet模型：

m = Prophet(
holidays=pd.DataFrame({
  'holiday': '618',
  'ds': pd.to_datetime(['2021-06-18', '2022-06-18', '2023-06-18', '2024-06-18']),
  'lower_window': -1,
  'upper_window': 0,
  'mode': 'additive'
})) 


model.add_seasonality({'name':'seasonal_1','period':7, 'fourier_order':1,'mode': 'additive'})
model.add_seasonality({'name':'seasonal_2','period':365, 'fourier_order':2,'mode': 'multiplicative'})

假设yearly傅立叶阶数为1的additive，weekly阶数为2的additive函数，那么component_cols为：

设置间断点

python.Prophet.forecaster.Prophet.set_changepoints

首先当有人工设置间断点时，以设置的间断点为主，间断点必须在训练数据之内，否则会报错。

当没有设置间断点时，Prophet会根据初始化的参数n_changepoints间断点数和changepoint_range间断点筛选范围，进行自动采样。例如时间序列有100个点，n_changepoints=10，changepoint_range=0.8，那么Prophet会在前80个点中，等间隔的采样10个点，作为候选间断点。设置的间断点数量不能超过changepoint_range范围内的训练集数量。

初始化stan参数

python.Prophet.forecaster.Prophet.calculate_initial_params

使用贝叶斯估计参数，需要给定参数的初始值，然后迭代至算法收敛，Prophet用全部训练数据计算初始参数。每一项成分都需要进行参数初始化。

以线性趋势为例，用标准化的y计算线性函数的斜率和偏置。其他回归项因子β，突变点增长系数δ都设置为0。

参数拟合

在初始化阶段得到的参数和数据，转化成字典形式传入Stan进行参数拟合，字典格式如下所示：

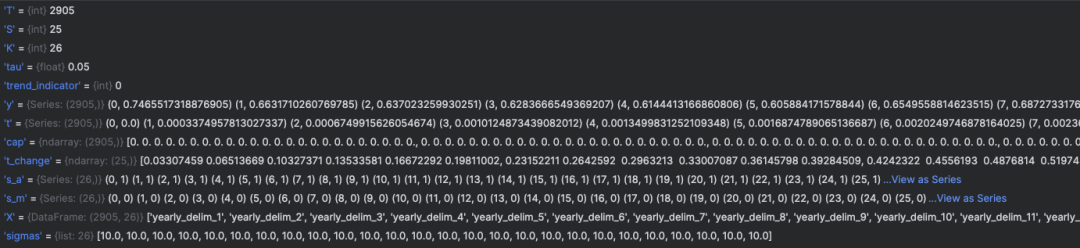
字典K-V值和Prophet/stan目录下的Prophet.stan脚本相对应，然后通过Pystan调用Stan引擎求解参数，拟合后的参数存储在Propeht.params中，求解参数有两种方式：

• 牛顿法/LBFGS法进行最大后验估计

python.Prophet.models.CmdStanPyBackend.fit

• 马尔可夫链蒙特卡罗法算法进行参数估计

python.Prophet.models.CmdStanPyBackend.sampling

预测过程

构建预测dataframe

python.Prophet.forecaster.Prophet.make_future_dataframe

我们可以通过Prophet类中的make_future_dataframe函数构建未来预测的DataFrame，预测长度、预测频率由初始化参数periods、freq设置。

构建预测的DataFrame之后，和在训练过程一致，需经过数据检查、归一化，归一化使用训练过程中计算得到的y_scale和回归项的均值和标准差。

点预测

点预测也就是在时间点上输出单个预测值，预测值由趋势预测和回归项预测组成。

• 趋势预测

python.Prophet.forecaster.Prophet.predict_trend

在贝叶斯回归中，未知参数服从一个指定的先验分布，Prophet使用Stan引擎计算得到的返回参数的期望作为趋势项公式的带入值。

def predict_trend(self, df):
    k = np.nanmean(self.params['k'])
    m = np.nanmean(self.params['m'])
    deltas = np.nanmean(self.params['delta'], axis=0)


    t = np.array(df['t'])
    if self.growth == 'linear':
        trend = self.piecewise_linear(t, deltas, k, m, self.changepoints_t)
    elif self.growth == 'logistic':
        cap = df['cap_scaled']
        trend = self.piecewise_logistic(
            t, cap, deltas, k, m, self.changepoints_t)
    elif self.growth == 'flat':
        # constant trend
        trend = self.flat_trend(t, m)


    return trend * self.y_scale + df['floor']

复制

对于flat、linear、logistic不同的趋势分量，结合changepoints_t进行趋势的预测，以线性趋势为例。

python.Prophet.forecaster.Prophet.piecewise_linear

即论文中描述的公式：

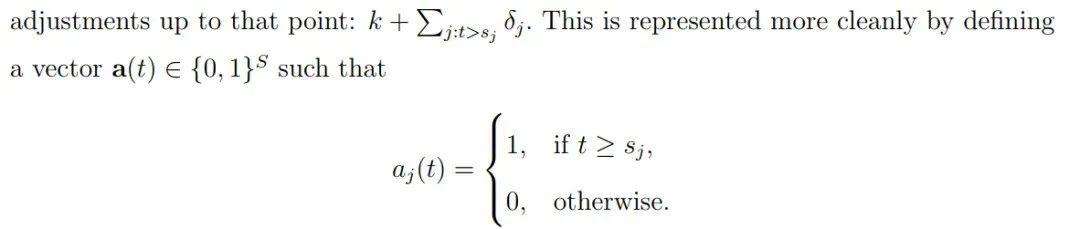
最后根据训练过程计算的y_scale缩放变量还原量级，作为最终的趋势预测。

• 回归项预测

python.Prophet.forecaster.Prophet.predict_seasonal_components

上文提到的Prophet的seasonality features、holiday features和add regressors项，在参数求解过程中是一样处理方法。

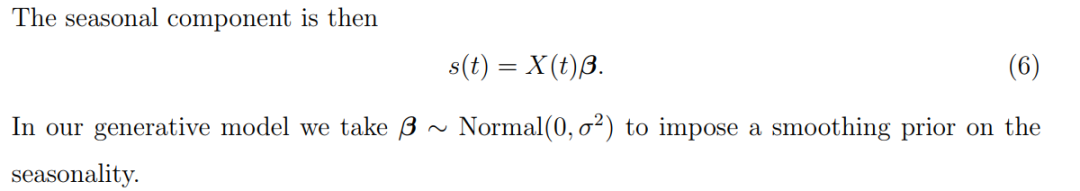
β即为拟合出的权重系数，β乘以特征宽表对应的值，得到每个特征的效应值。根据component_cols维护的不同成分的特征归属。就可以得到seasonality、holiday features、add regressors、multiplicative_terms、additive_terms各个部分的效应值。这些在模型解释性、结果可视化、偏差分析中都可以应用。

• 预测汇总

python/Prophet/forecaster.py:1287

预测成分汇总步骤把趋势、季节性、节假日等预测效应值进行拼接，最后的预测结果公式如下：

预测结果值=趋势*(1+乘法因素)+加法因素

预测的不确定性

Prophet通过观测噪声、参数不确定性以及未来趋势不确定性三个部分输出预测值的不确定性，最终通过yhat_lower、yhat_upper体现。

• 观测噪声不确定性

python/Prophet/forecaster.py:1556

一般时间序列分解模型，最后的一个分解项就是噪声，Prophet也是这样的，假设了输入数据点含有服从正态分布的观测噪声，Stan模型脚本中的sigma_obs就是拟合了这部分噪声。观测噪声不确定性为：

sigma = self.params['sigma_obs'][iteration]
noise_terms = np.random.normal(0, sigma, trends.shape) * self.y_scale

复制

变量sigma是sigma_obs的估计值。在每个时间步骤上，从正态分布中采样n_samples次，得到噪声不确定项目noise_terms。

• 趋势不确定性

python.Prophet.forecaster.Prophet._make_trend_shift_matrix

对于趋势的不确定性，官方文档中解释：预测中最大的不确定性来源在于未来趋势变化的可能性。因此我们尽最大可能采取了一个合理的假设，假设未来的趋势变化会与历史上观察到的相似。特别是，我们假设未来的趋势变化的平均频率和幅度将与历史上观察到的相同。我们将这些趋势变化进行投影，并通过计算它们的分布来获得不确定性区间。

具体而言，趋势不确性由突变点出现的位置和突变的比例确定。首先计算历史上突变点出现的间隔的均值*历史上突变点的个数，得到每个时间点上产生突变点概率likelihood。然后计算历史突变点的变化率的绝对值的均值mean_delta。最后进行采样来模拟不确定性。均匀分布采样输出矩阵（n_samples, future_length），对每一个元素判断是否小于似然值likelihood，来判断是否发生了突变，如果小于则发生了突变，然后输出均值为mean_delta的拉普拉斯分布，得到突变点变化率的采样值。

• 参数的不确定性

python.Prophet.forecaster.Prophet.predict_uncertainty

当初始化参数MCMC=0，即调用Stan用MAP算法，此时算法得出的是收敛时的最终估计值，不确定性由观测不确定性和趋势不确定性组成，参数没有不确定性的估计。

MCMC>0时候，除了观测噪声、趋势不确定性外，由于Stan采用MCMC采样方法，得到的返回值是待估计参数值的若干个采样点，根据每个参数的采样点得到不同的预测值。

• 不确定性结果输出

进一步，由于每一个时间步有以上不确定性成分的n_samples个采样数据。根据预设的置信度宽度，得到上、下分位数值：

lower_p = 100 * (1.0 - self.interval_width) / 2
upper_p = 100 * (1.0 + self.interval_width) / 2

复制

对于每个时间步骤，求lower_p分位数、upper_p分位数，即得到yhat_lower、yhat_upper。

四、总结

Prophet框架在有明显规律的单变量时序预测场景中有着非常不错的表现。在得物的多个业务场景中已经得到了验证。阅读源码能够帮助我们更好的了解模型细节，在模型优化时帮助我们有的放矢，在模型选型时帮助我们掌握模型的适应性和局限性。

参考资料

​​https://peerj.com/preprints/3190/​​

​​https://github.com/facebook/prophet​​

​​https://zhuanlan.zhihu.com/p/37543542​​

本文转载自 ​​得物技术​​，作者： 探流