Meta 新作:FlashAttention 的数值偏差有多大?
一、背景
最近 Meta 的研究员开发了一个新的框架来了解 LLM 训练中数值偏差的影响,并基于该框架评估了 LLM 中广泛采用的 FlashAttention 的数值偏差。
对应的论文为:[2405.02803] Is Flash Attention Stable?
PS:其实论文很简单,结论也很简单:使用 FlashAttention 相比 Baseline Attention 确实会带来数值偏差。但带来的数值偏差比从 FP32 到 FP16 的数值偏差小得多,甚至小于不同初始化方法带来的偏差。吐槽一下,论文中的图都比较模糊。
二、摘要
LLM 预训练的代价很高,也更加的复杂。很多 LLM 在预训练中都遇到了训练过程不稳定的情况,通常表示为损失的毛刺(Spike)。数值偏差(Numeric Deviation)被认为是导致这种训练不稳定的潜在原因,但由于训练的成本很高,量化这一点非常有挑战性。
本文中,作者开发了一种系统性的方法来理解数值偏差的影响,并使用广泛采用的 FlashAttention 来验证了该框架。作者发现,与 Baseline Attention 相比,在单个前向传播中,BF16 下的 FlashAttention 会有超过一个数量级的数值偏差。然而,使用基于 Wasserstein 距离的数据驱动分析来提供数值偏差对训练过程中模型权重影响的上限,发现 FlashAttention 中的数值偏差比低精度训练的影响小 2-5 倍。
三、引言
3.1 数值精度
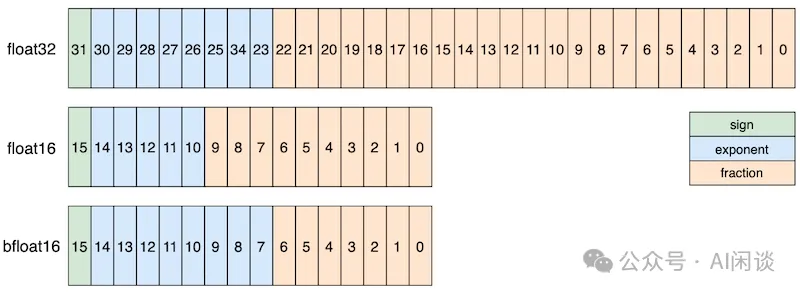
如下图为常见的浮点数值精度,其中 sign 表示符号位,exponent 表示指数位,fraction 表示尾数位。相比 float32,float16 的指数位和尾数位都更小,而 bfloat16 的指数位和 float32 相同,只是尾数位更少。因此,通常 float32 转 float16 时通常会带来较大的精度损失,而 float32 转 bfloat16 通常只需要做小数位的截断,损失相对较小。现在的 LLM 预训练中通常都会使用 bfloat16。
- Float32:指数位 8 位,尾数位 23 位,数据范围为[1.18e-38, 3.40e+38]
- float16:指数位 5 位,尾数位 10 位,数据范围为[6.10e-05, 6.55e+04]
- bfloat16:指数位 8 位,尾数位 7 位,数据范围为[1.18e-38, 3.39e+38]
3.2 数值误差
在浮点数的计算中会存在两种常见的误差:
- 溢出误差(Overflow Error):浮点都有一个有限的表示范围,当计算结果超出这个表示范围时就会产生溢出错误,往往表现为无穷大。比如,令 float a = FLT_MAX * 2,此时 a 的值为正无穷大。
- 舍入误差(Rounding Error):浮点数有固定的有效位数,当一个数值不能被精确表示时,就会被舍入到最接近的可表示的浮点数。这种输入在数值计算中是不可避免的,因为大多数实数在计算机中无法被精确表示。比如在 C 中打印 0.1f,printf("a = %.20f\n", 0.1f),其输出结果为 0.10000000149011611938,是一个近似值。
除此之外,有时也会提到下溢误差(Underflow Error):当一个非常小的非零结果小于浮点数表示范围下限时发生,通常导致结果被舍入为零。
由于 float16 和 bfloat16 的不同指数位和尾数位,也就导致它们出现误差的场景不太一样。
- float16:指数位较少,尾数位较多,表示范围有限,但表示精度更高,因此更容易发生溢出误差。
- bfloat16:指数位较多,尾数位较少,表示范围更大,但表示精度有限,因此更容易发生舍入误差。下溢误差也更多一些。
3.3 训练损失毛刺
在 Meta OPT、BigScience Bloom、Google PaLM、TII Falcon 以及智源 GLM 训练中都出现了训练损失出现毛刺的情况,也有一些有效的手段可以缓解,但依旧不知道其根因。比如 Google PaLM 中验证了其并非是单个样本导致的。
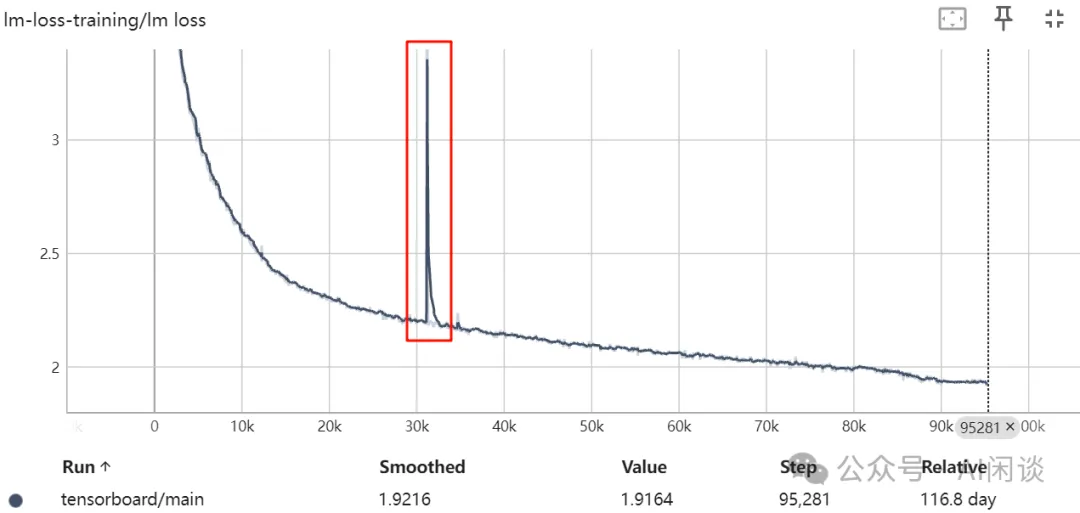
如下图所示,是 [2211.05100] BLOOM: A 176B-Parameter Open-Access Multilingual Language Model 中遇到的毛刺现象:
3.4 评估指标
Wasserstein 距离,也称为 Earth Mover’s Distance (EMD),是一种衡量两个概率分布之间差异的方法。这种距离的直观含义是,将一个概率分布转变成另一个概率分布所需要的“工作量”或“成本”,其中“工作量”可以理解为将一堆形状不同的沙子(一个概率分布)铲动并重塑为另一堆沙子(另一个概率分布)所需要的努力。
Wasserstein 距离基于最优运输理论。给定两个概率分布 P 和 𝑄,以及一个成本函数 𝑐(𝑥,𝑦),Wasserstein 距离定义为将分布 P 转变为 Q 所需的最小成本。数学上,它表示为:

这里的 π 是 P 和 𝑄 之间的所有可能的联合分布的集合,而 Π(P,Q) 表示所有这些联合分布中,边际分布分别是 P 和 Q 的集合。
相比其他距离度量(如欧氏距离或 KL 散度),Wasserstein 距离的一个主要优势在于其能够更加有效地处理概率分布之间的微小变化,特别是当这些分布不重叠或仅部分重叠时。这使得 Wasserstein 距离在数据稀疏或异构的情况下特别有用。
四、方法&实验
4.1 方法
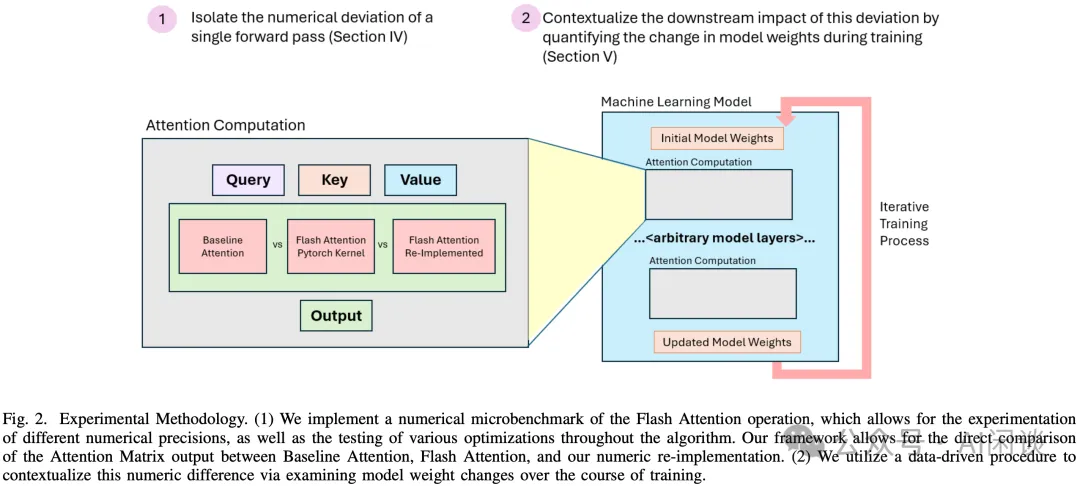
作者开发了一个 microbenchmark 来隔离和研究 FlashAttention 引起的数值偏差。其设计如下图 Fig 2 所示,在原始的 FlashAttention 中只支持 FP16 和 BF16 格式,因此作者重新实现了 FlashAttention,以便分析不同的数值精度的影响。作者进一步修改模型,可以在每次调用 Attention 时计算 Baseline Attention 和 FlashAttention 的注意力矩阵输出,从而可以使用最大差异(max difference)以及 Wasserstein 距离来度量差异。作者也进行了一系列训练来度量整个训练过程中模型权重的差异。
4.2 数据类型的影响
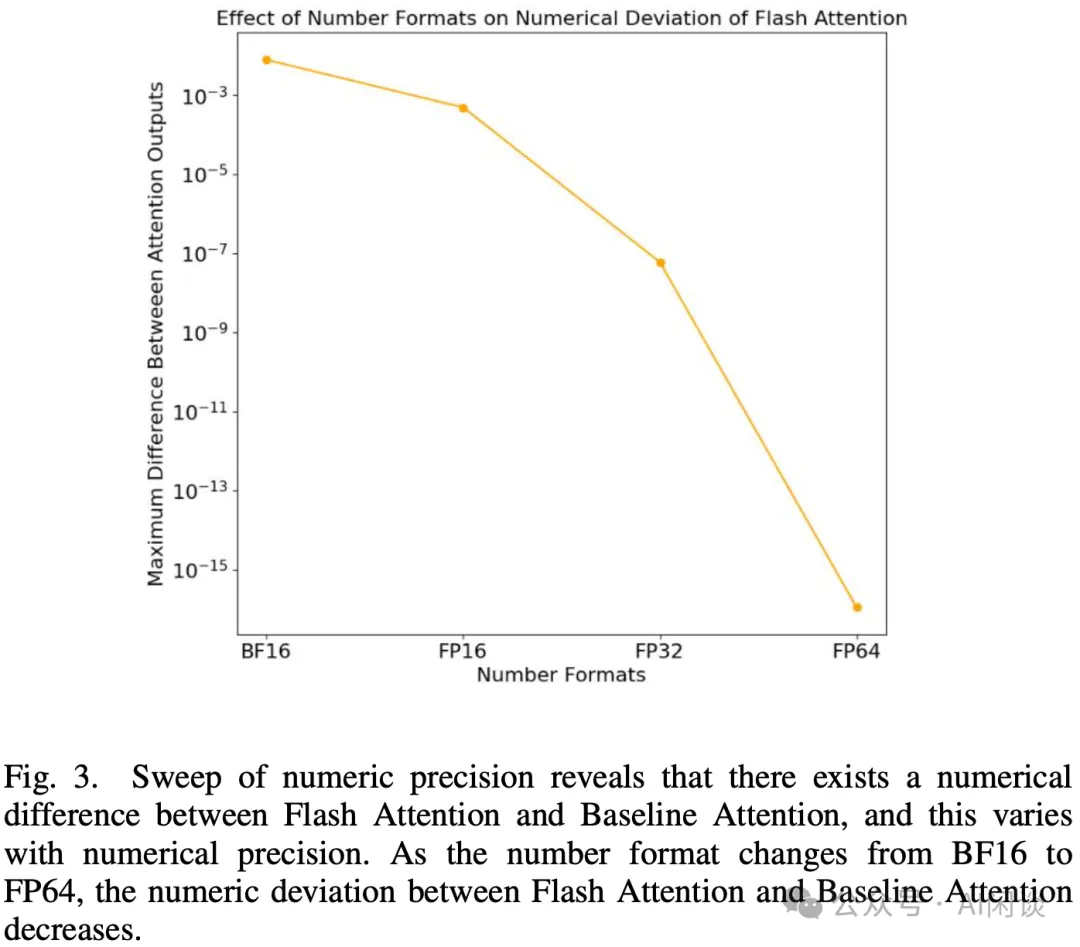
如下图 Fig.3 所示,作者对比了不同数据类型下 Baseline Attention 和 FlashAttention 的数值偏差,可以看出,数值精度越高,偏差越小:
为了进一步分析这种数值偏差,作者探索了序列长度对数值偏差的影响,其中会保持 FlashAttention 的 tile 大小和 SRAM 大小相同。如下图所示,随着序列长度的增加,数值偏差也会适当增加。其中左图(a)表示最大误差,右图(b)表示误差的均值。由于序列变长,也就需要更多的 tile,相应也有更多的 resaling,这也就可能产生更多的误差:
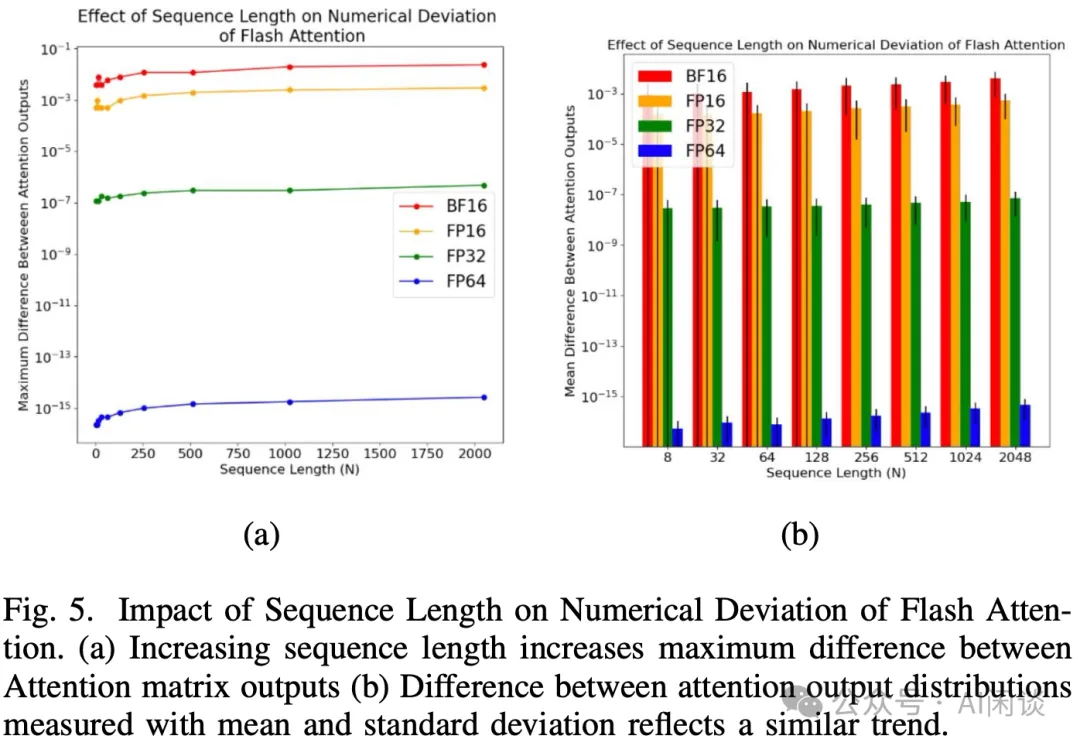
4.3 算法配置的影响
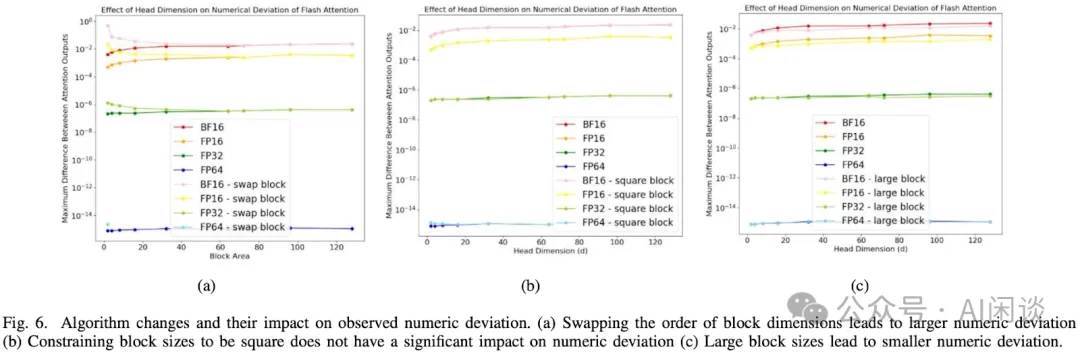
如下图 Fig 6 所示,作者进一步探索了 FlashAttention 中不同配置的影响:
- (a)和(c)针对不同的 Block/tile Area 大小的影响,使用比较大的 Block 后 Baseline Attention 和 FlashAttention 的差异很小,主要是因为 rescaling 计算更少一些。
- (b)使用 Square Block 对 Baseline Attention 和 FlashAttention 的影响不大。
4.4 模型权重的变化
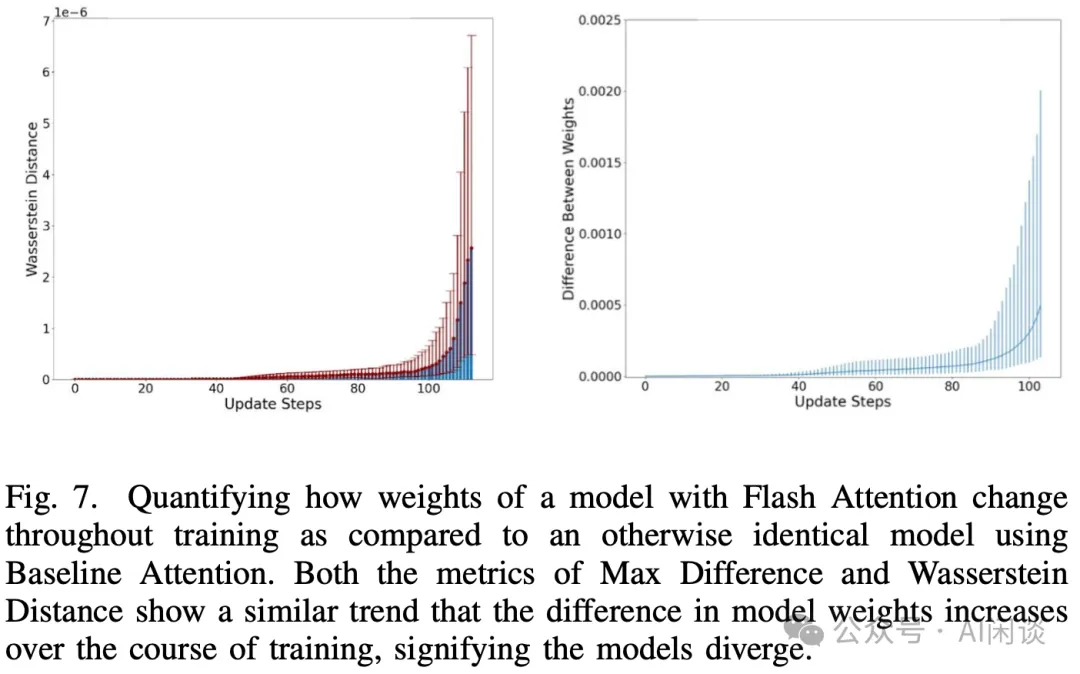
作者进一步验证了训练中模型权重的变化(对比 Baseline Attention 和 FlashAttention),如下图 Fig 7 所述,不管是最大误差还是 Wasserstein 距离都会随着训练的迭代而逐渐变大,并且趋势类似:
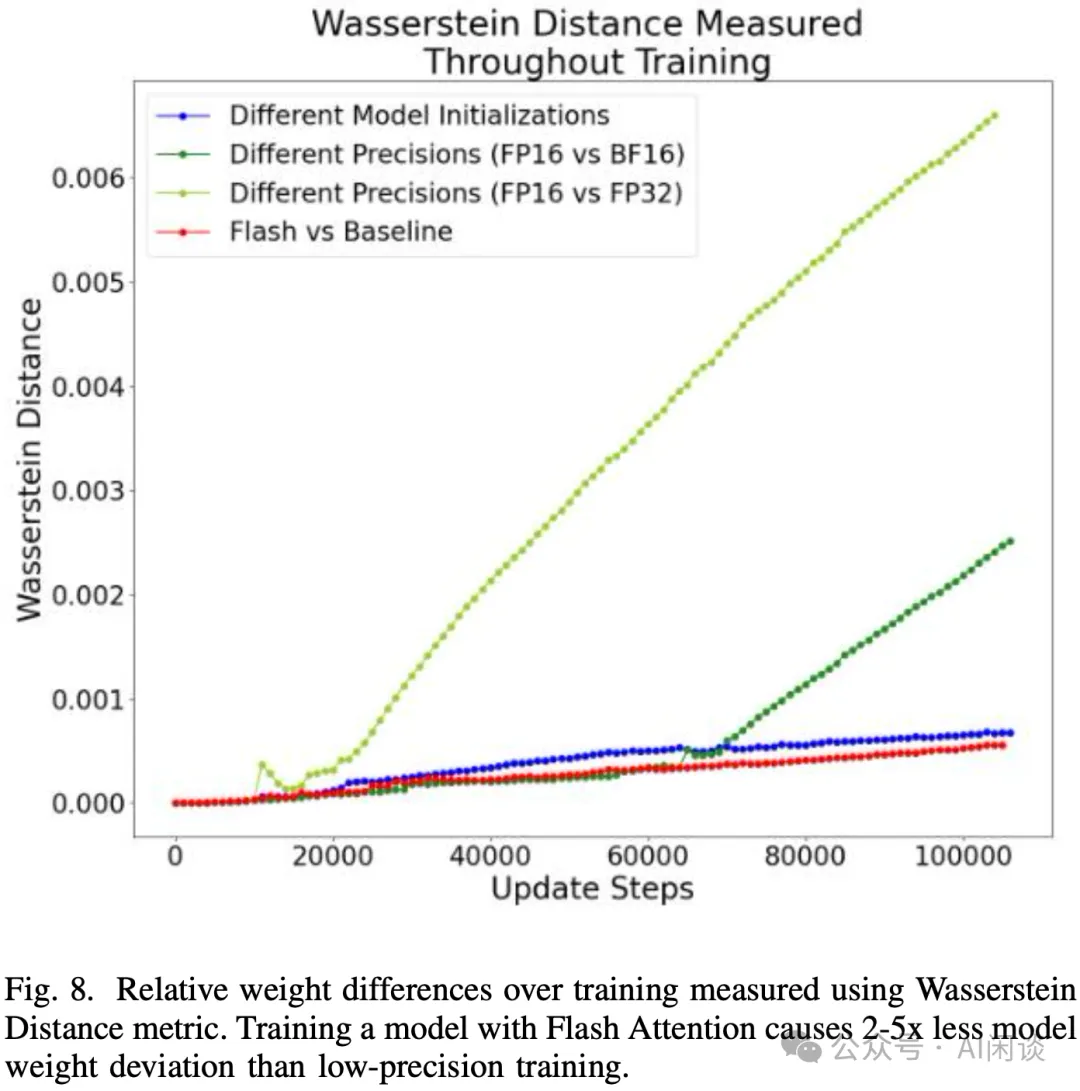
如下图 Fig.8 所示,作者进一步验证了整个训练中其他变量带来的模型权重的偏差。可以看出,虽然 Baseline Attention 和 FlashAttention 会导致权重产生误差,但是其甚至比不同初始化方法带来的误差还小,更是远小于 FP16 vs BF16 和 FP16 vs FP32 带来的误差:
五、参考链接
本文转载自 AI闲谈,作者: AI闲谈

















