TPAMI 2024 | 针对节点的融合全局-局部信息的图谱滤波方法

论文题目:
Node-oriented Spectral Filtering for Graph Neural Networks
论文作者:
Shuai Zheng, Zhenfeng Zhu, Zhizhe Liu, Youru Li, Yao Zhao
作者单位:
北京交通大学
源码链接:
https://github.com/SsGood/NFGNN/
论文链接:
https://ieeexplore.ieee.org/abstract/document/10286416/
01 研究背景
在图机器学习领域中,同配性(homophily)一直是一个普遍的假设,即属于同一类的节点倾向于互相连接。然而,这一假设在很多真实的图相关场景中其实并不成立,蛋白质结构网络就是一个很典型的例子。
因此,研究面向异配图数据的图神经网络在近几年成为了领域内的一大主题。考虑到同配性的定义,我们提出一个观点:下游任务与构建图时所采用的先验的相关性决定了一个图的同配性程度。
具体来说,对于一个给定的拓扑结构,当其与不同下游任务的标签分布相结合时,其同配性程度可能会非常不同。例如,学术引用网络中,因为一篇论文更有可能引用研究相同或类似主题的论文,所以引文网络链接的形成与主题分类任务是强正相关的。因此,如果我们使用论文的主题作为标签,则则该网络可能是同配性的;而如果我们以论文的发布年份作为标签,引用图可能是异配性或随机的。
以上述假设看待图的同配性问题,我们会发现,在标签有限的情况下,下游任务与图结构之间的相关性是较难预测的。因此,一个自然而然的问题是:整个图中不同局部子图的同配程度是否一致?
直观上,假设不同区域之间总是存在多样的子图模式可能更为现实。因此,相比于特定于同配图或异配图的聚合设计,一种可以自适配图中不同局部同配模式的 GNN,可能是更贴近实际应用需求的。
与基于空域聚合的方法相比,基于频谱的图神经网络具有出色的理论解释性和计算效率。然而,当前基于谱滤波的方法均采用了全局共享单一滤波器的学习方式。本文中,我们基于图信号处理理论,首次尝试探索局部自适应的谱滤波学习,以解决图中的混合局部模式。
本文的主要贡献如下:
- 为了深入了解实际图的高阶混合模式以及 GNN 对它们的适应性,我们从子图同配随机性和近邻可聚合性两个方面进行了实证和理论分析。
- 受广义平移算子的启发,我们提出了一种面向节点的谱滤波 GNN,即 NFGNN。它充分考虑了过滤器定位节点的局部子图模式来估计滤波系数。
- 为了减轻学习面向节点的局部滤波系数的繁重负担,我们提出了一种基于低秩近似的重参数化方法来分解滤波系数矩阵,不仅简化了参数复杂度,而且在全局滤波和局部滤波之间进行了权衡。
02 局部同配模式分析
2.1 子图同配随机性
由于目标是通过节点邻域的标签一致性来分析图的局部同配模式,因此我们采用了节点同配率来分析局部同配模式。首先,我们给出一阶邻域同配率和二阶邻域同配率的节点级统计直方图的可视化。
如图 1 所示,即使在通常被认为是同配性图的 Cora 和 Citeseer 网络中,也仍然存在少量的 1 跳完全异配子图。同样,在 Cornell 和 Actor 网络中也有一些高同配率的子图。此外,对于 Cornell 和 Actor 网络,我们发现二阶邻域同配率统计直方图与一阶统计结果的显示出一定的偏移,表明每个节点关联的局部子图模式通常随着邻域范围的变化而变化。
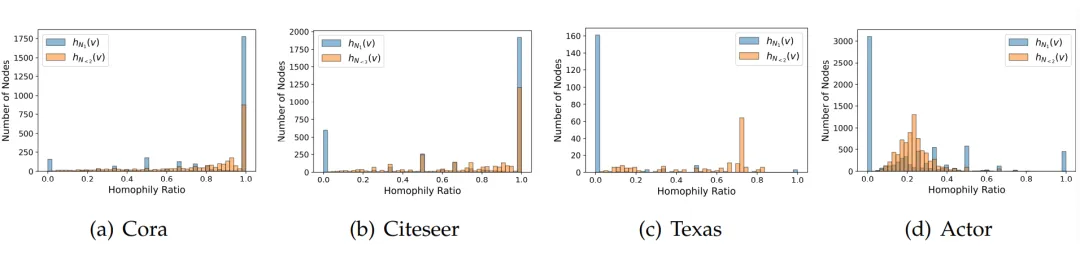
▲ 图1:一阶邻域同配率和二阶邻域同配率的节点级统计直方图的可视化。
值得注意的是,节点同配率的计算仅能简单传达邻域节点和中心节点的标签一致性,但忽略了邻域标签是呈现什么样的分布,这对局部模式分析同样重要。受信息论中香农熵的启发,我们提出使用标签熵 来衡量邻域标签分布:
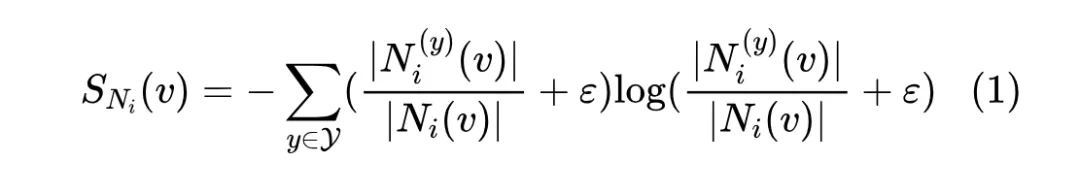
其中,,1e-10 是一个常数,用以避免溢出。标签熵作为节点级指标,量化了给定节点的邻域标签分布,并指示了以该节点为中心的子图的随机性。显然,当邻居节点的标签分布均匀时,标签熵趋于最大。相反,如果给定节点的邻域标签全部属于同一类,则标签熵将是最小的。
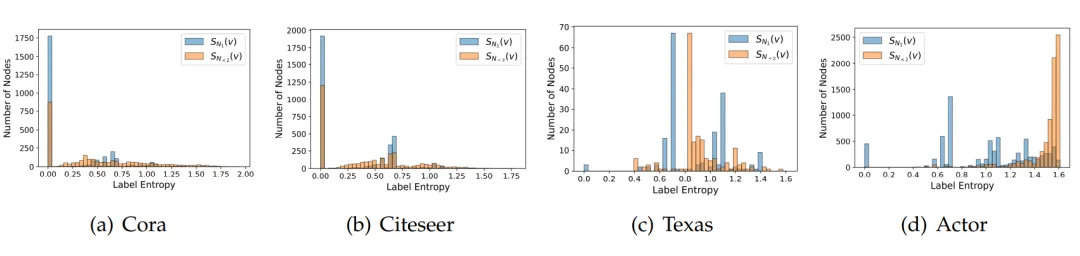
▲ 图2:一阶邻域标签熵和二阶邻域标签熵的节点级统计直方图的可视化。
如图 2 所示,同配性图中的大多数节点的 较低,而异配性图中的大多数节点的 较高。此外,对于所有四个图,与 相比, 的统计直方图总体上向右移动。这些观察表明,随着邻域范围的增加,每个节点的邻居标签分布趋于均匀。更重要的是,从图 2(c)和(d)中,可以容易地发现一些明显的聚类现象,表明图中可能存在几种类型的重要局部模式。
2.2 近邻可聚合性
为了便于讨论近邻的可聚集性,我们首先给出邻域同配倾向性的定义:

我们首先理论证明了邻域同配倾向性和邻域标签分布的关系:

随即,我们还给出了随邻域范围变化,邻域同配倾向性的变化趋势:
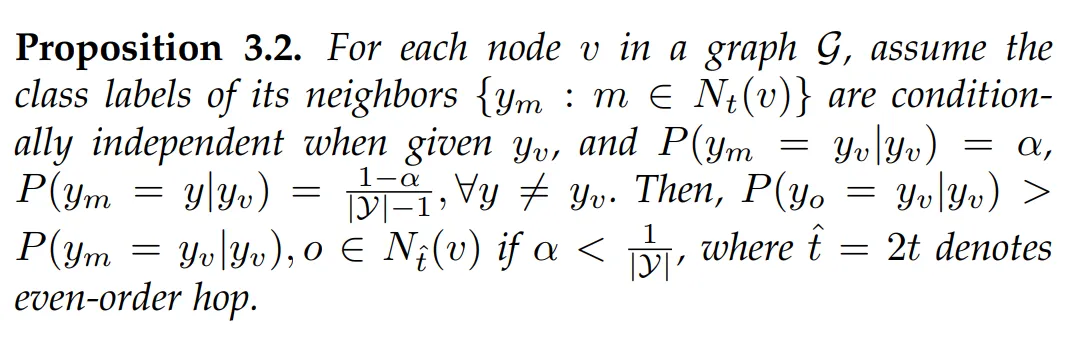
具体证明过程可见论文。
03 方法介绍
当前基于谱滤波的图神经网络多采用多项式参数化滤波器学习的形式。这种形式避免了特征分解,计算效率较高。另一个优点就是具有局部性,多项式的阶数 K 决定了滤波器的局部化范围,即 K 阶多项式谱滤波器完全局限于节点 的 邻域内。
但是呢,当前基于谱滤波的方法有一个显著的特点:滤波器是全局节点通用的且频率系数固定的单一滤波器。这个特点和多项式滤波的局部性结合在一起,就产生了新的问题:全局共享的单一滤波器相当于是在不同子图上训练的滤波器的trade-off。对于每个以节点为中心的子图而言,这个全局滤波器肯定不是最差的,但应该也不是最优的。
直观上,与学习整个图中不同局部模式的全局共享滤波器 相比,学习特定于节点的节点滤波器 以适应其所在的局部模式似乎是更好的选择。为此,本文重新思考这种全局一致的谱图滤波形式,并尝试提出一种局部化的谱滤波器学习方法来打破这一限制。
NFGNN 首先引入图信号处理中的广义平移算子 :
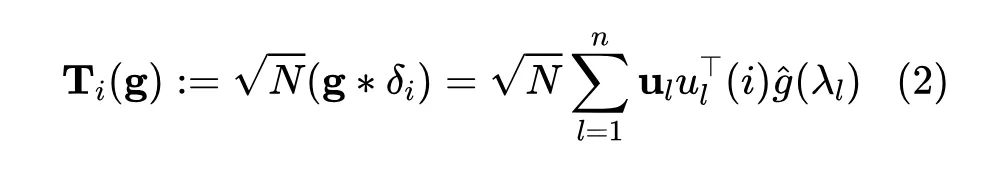
其中 表示 的第 个元素。通过对滤波信号 施加核化算子,可以使其定位在特定节点上。因此,为了自适应局部滤波的目的,首先可以通过 将滤波器信号 定位到在目标节点 上,将其定义为 ,然后与 执行谱滤波:
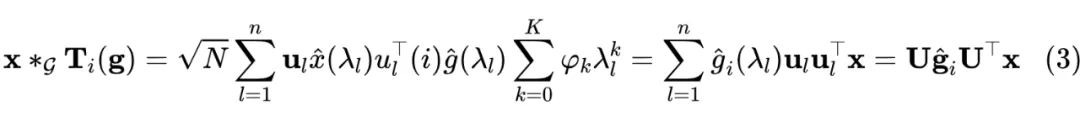
其中 ,那我们为了计算的效率问题,进一步地用多项式来参数化 ,从而得到节点导向的局部化滤波形式:
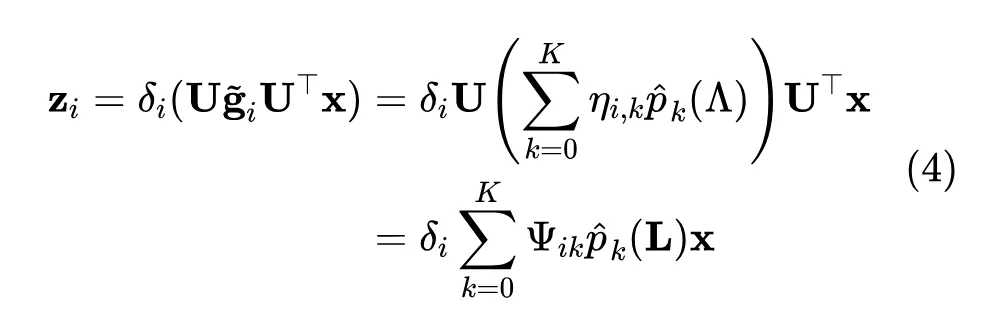
进一步地,考虑到滤波系数矩阵 的参数复杂度和优化问题,我们对其进行低秩逼近重参数化。 由两个可训练参数矩阵 近似,其中 和 。
可以很容易地观察到,。这意味着 的每一列都可以视为 。因此, 相当于一组基础滤波器,而 对应于节点 的滤波器权重。
根据 ,通过对 中的基础滤波器进行加权组合,可以获得专用于 的滤波器。所以,对于 ,由于其可以视为与节点相关的参数,我们应用了一个简单但有效的非线性变换 来学习:。
04 实验
我们在多个基准数据集上进行了全面的实验,以评估所提出的方法的有效性。
4.1 性能对比
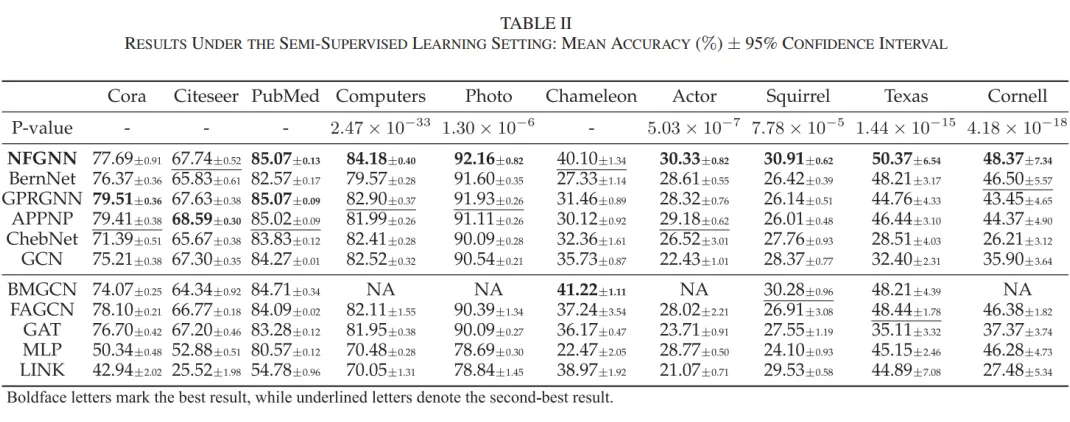
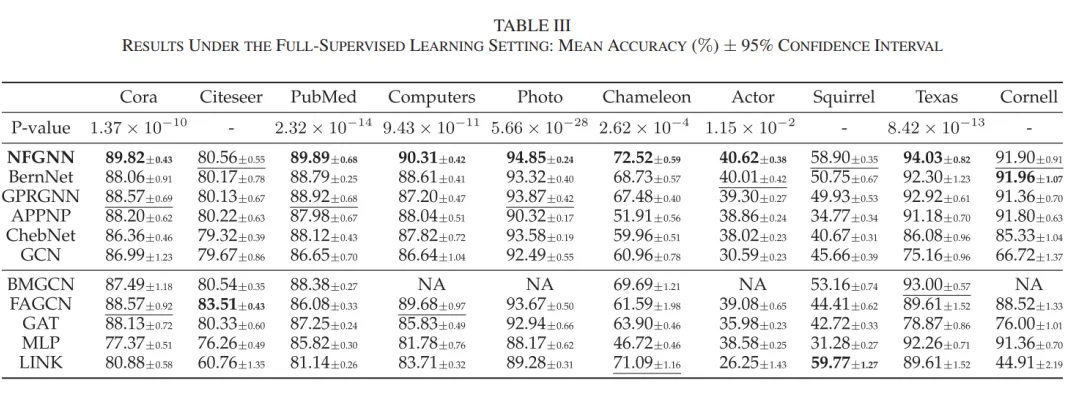
在采用稀疏划分的半监督学习中,NFGNN 在 6 个数据集上表现出色,并在剩余的 4 个数据集上与基准模型相比显示出可比结果。此外,在全监督学习设置下,NFGNN 在 7 个数据集上优于所有基准模型,在其他 3 个数据集上取得了可比结果。
4.2 节点级分析
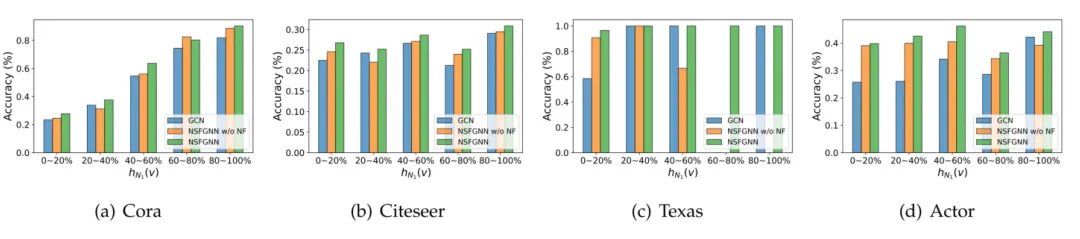
▲ 图3 不同同配比例区间内的节点分类准确率。
本文提出的 NFGNN 旨在解决混合局部模式问题。因此,我们根据邻近节点的同配性比例 将测试节点划分为 5 个不同区间,并报告每个区间的平均准确率。GCN、仅有 的 NFGNN(标记为 NFGNN w/o NF)和完整的 NFGNN 的结果如图 3 所示。
值得注意的是,NFGNN w/o NF 相当于使用切比雪夫多项式学习一个全局一致的滤波器。
与 GCN 不同,如图 3(c)和(d)所示,NFGNN 在所有五个区间上均表现出了良好且相似的性能。这表明,只要可训练数据量足够,NFGNN 可以有效捕获各种局部模式。
此外,如图 3(a)和(b)所示,无论是 NFGNN 还是 NFGNN w/o NF 都比 GCN 在半监督节点分类任务上表现更好。这表明,即使在半监督情况下,自适应学习的滤波器也不比预设计的滤波器表现差。
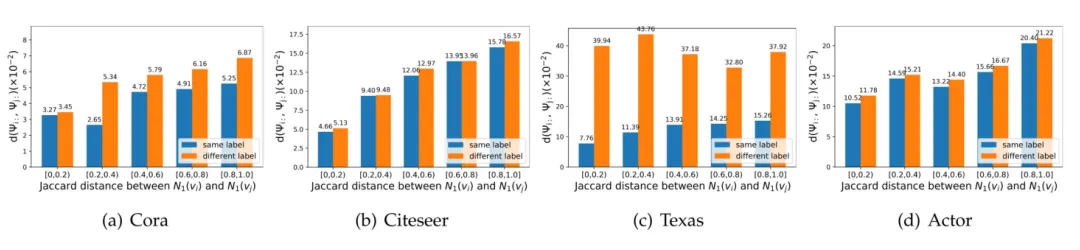
▲ 图4 节点对 之间的滤波系数平均距离 。
正如之前讨论的,局部模式也可以根据节点的邻域子图来分析。一般来说,如果节点的局部模式相似,那么为这些节点学习的滤波器的系数也应该相似。因此,本文中还计算了所有节点对 的 1 阶邻居的 Jaccard 相似系数 ,以衡量节点之间 1 阶局部模式的相似性,然后,对于每对节点 ,根据 的区间计算平均系数距离 。
如图 4 所示,总的来说,可以看到, 越大,相应的 越大。并且,具有相同标签的节点对的 小于具有不同标签的节点对。可视化结果表明,NFGNN 至少能够学习到多种1跳局部模式的特性,符合预期。
4.3 滤波器可视化
首先根据 2 跳邻域内的同配比率将节点划分为三个子集:
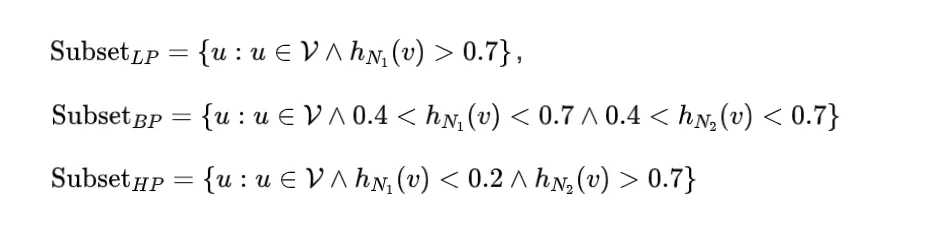
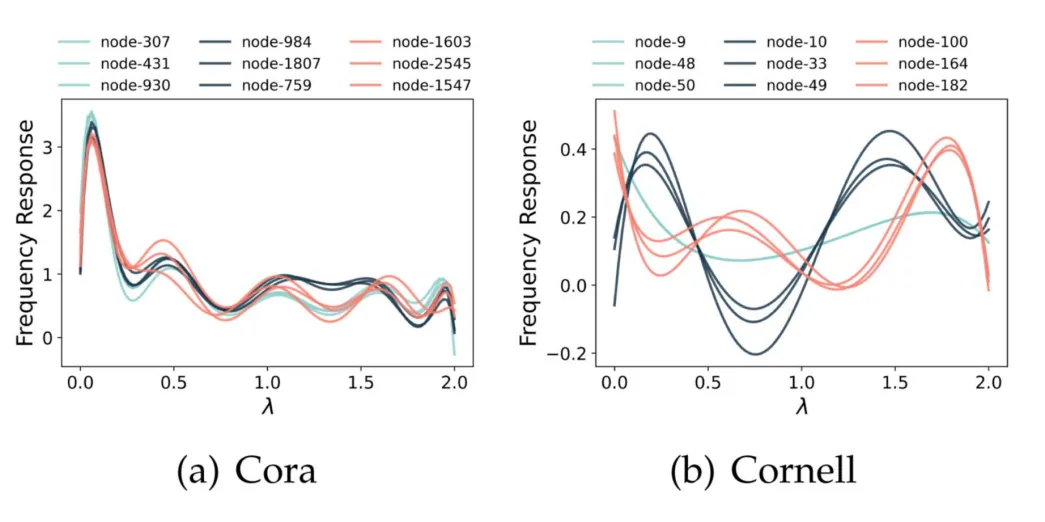
▲ 图5 节点级滤波器可视化
05 总结
本文深入分析了图数据中局部模式的特性及其近邻的可聚合性。基于这些观察,本章重新审视了基于谱的图神经网络(GNN)模型,并提出了 NFGNN ——一种针对节点的融合全局-局部信息的图谱滤波方法。NFGNN 的核心优势在于,它不同于传统使用全局滤波器的策略,而是通过转移至特定节点的滤波器来实现局部谱滤波,从而有效地应对局部模式的挑战。
此外,通过引入重参数化策略,NFGNN 以一种简单且有效的方式实现了节点导向的滤波。在多个真实世界的图数据集上进行的实验结果验证了 NFGNN 在当前现有方法中的卓越性能,展示了其在处理局部图模式方面的显著优势。

















