在神经网络中实现反向传播
建立神经网络时,需要采取几个步骤。其中两个最重要的步骤是实现正向和反向传播。这两个词听起来真的很沉重,并且总是让初学者感到恐惧。但实际上,如果将这些技术分解为各自的步骤,则可以正确理解它们。在本文中,我们将专注于反向传播及其每个步骤的直观知识。
什么是反向传播?
这只是实现神经网络的一项简单技术,允许我们计算参数的梯度,以执行梯度下降并使成本函数最小化。许多学者将反向传播描述为神经网络中数学上最密集的部分。不过请放轻松,因为在本文中我们将完全解密反向传播的每个部分。
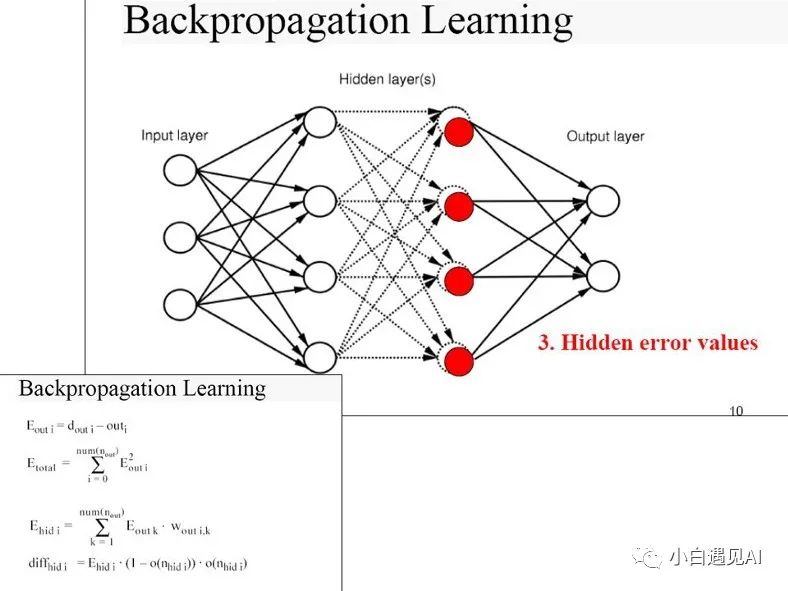
实施反向传播
假设一个简单的两层神经网络-一个隐藏层和一个输出层。我们可以如下执行反向传播初始化要用于神经网络的权重和偏差:这涉及随机初始化神经网络的权重和偏差。这些参数的梯度将从反向传播中获得,并用于更新梯度下降。
#Import Numpy library
import numpy as np
#set seed for reproducability
np.random.seed(100)
#We will first initialize the weights and bias needed and store them in a dictionary called W_B
def initialize(num_f, num_h, num_out):
'''
Description: This function randomly initializes the weights and biases of each layer of the neural network
Input Arguments:
num_f - number of training features
num_h -the number of nodes in the hidden layers
num_out - the number of nodes in the output
Output:
W_B - A dictionary of the initialized parameters.
'''
#randomly initialize weights and biases, and proceed to store in a dictionary
W_B = {
'W1': np.random.randn(num_h, num_f),
'b1': np.zeros((num_h, 1)),
'W2': np.random.randn(num_out, num_h),
'b2': np.zeros((num_out, 1))
}
return W_B执行前向传播:这涉及到计算隐藏层和输出层的线性和激活输出。
对于隐藏层:我们将使用如下所示的relu激活功能:
#We will now proceed to create functions for each of our activation functions
def relu (Z):
'''
Description: This function performs the relu activation function on a given number or matrix.
Input Arguments:
Z - matrix or integer
Output:
relu_Z - matrix or integer with relu performed on it
'''
relu_Z = np.maximum(Z,0)
return relu_Z对于输出层:
我们将使用S型激活函数,如下所示:
def sigmoid (Z):
'''
Description: This function performs the sigmoid activation function on a given number or matrix.
Input Arguments:
Z - matrix or integer
Output:
sigmoid_Z - matrix or integer with sigmoid performed on it
'''
sigmoid_Z = 1 / (1 + (np.exp(-Z)))
return sigmoid_Z执行前向传播:
#We will now proceed to perform forward propagation
def forward_propagation(X, W_B):
'''
Description: This function performs the forward propagation in a vectorized form
Input Arguments:
X - input training examples
W_B - initialized weights and biases
Output:
forward_results - A dictionary containing the linear and activation outputs
'''
#Calculate the linear Z for the hidden layer
Z1 = np.dot(X, W_B['W1'].T) + W_B['b1']
#Calculate the activation ouput for the hidden layer
A = relu(Z1)
#Calculate the linear Z for the output layer
Z2 = np.dot(A, W_B['W2'].T) + W_B['b2']
#Calculate the activation ouput for the ouptu layer
Y_pred = sigmoid(Z2)
#Save all ina dictionary
forward_results = {"Z1": Z1,
"A": A,
"Z2": Z2,
"Y_pred": Y_pred}
return forward_results执行向后传播:相对于与梯度下降相关的参数,计算成本的梯度。在这种情况下,为dLdZ2,dLdW2,dLdb2,dLdZ1,dLdW1和dLdb1。这些参数将与学习率结合起来执行梯度下降。我们将为许多训练样本(no_examples)实现反向传播的矢量化版本。
分步指南如下:
- 从传递中获取结果,如下所示:
forward_results = forward_propagation(X, W_B)
Z1 = forward_results['Z1']
A = forward_results['A']
Z2 = forward_results['Z2']
Y_pred = forward_results['Y_pred']- 获得训练样本的数量,如下所示:
no_examples = X.shape[1]- 计算函数的损失:
L = (1/no_examples) * np.sum(-Y_true * np.log(Y_pred) - (1 - Y_true) * np.log(1 - Y_pred))- 计算每个参数的梯度,如下所示:
dLdZ2= Y_pred - Y_true
dLdW2 = (1/no_examples) * np.dot(dLdZ2, A.T)
dLdb2 = (1/no_examples) * np.sum(dLdZ2, axis=1, keepdims=True)
dLdZ1 = np.multiply(np.dot(W_B['W2'].T, dLdZ2), (1 - np.power(A, 2)))
dLdW1 = (1/no_examples) * np.dot(dLdZ1, X.T)
dLdb1 = (1/no_examples) * np.sum(dLdZ1, axis=1, keepdims=True)- 将梯度下降所需的计算梯度存储在字典中:
gradients = {"dLdW1": dLdW1,
"dLdb1": dLdb1,
"dLdW2": dLdW2,
"dLdb2": dLdb2}- 返回损耗和存储的梯度:
return gradients, L这是完整的向后传播功能:
def backward_propagation(X, W_B, Y_true):
'''Description: This function performs the backward propagation in a vectorized form
Input Arguments:
X - input training examples
W_B - initialized weights and biases
Y_True - the true target values of the training examples
Output:
gradients - the calculated gradients of each parameter
L - the loss function
'''
# Obtain the forward results from the forward propagation
forward_results = forward_propagation(X, W_B)
Z1 = forward_results['Z1']
A = forward_results['A']
Z2 = forward_results['Z2']
Y_pred = forward_results['Y_pred']
#Obtain the number of training samples
no_examples = X.shape[1]
# Calculate loss
L = (1/no_examples) * np.sum(-Y_true * np.log(Y_pred) - (1 - Y_true) * np.log(1 - Y_pred))
#Calculate the gradients of each parameter needed for gradient descent
dLdZ2= Y_pred - Y_true
dLdW2 = (1/no_examples) * np.dot(dLdZ2, A.T)
dLdb2 = (1/no_examples) * np.sum(dLdZ2, axis=1, keepdims=True)
dLdZ1 = np.multiply(np.dot(W_B['W2'].T, dLdZ2), (1 - np.power(A, 2)))
dLdW1 = (1/no_examples) * np.dot(dLdZ1, X.T)
dLdb1 = (1/no_examples) * np.sum(dLdZ1, axis=1, keepdims=True)
#Store gradients for gradient descent in a dictionary
gradients = {"dLdW1": dLdW1,
"dLdb1": dLdb1,
"dLdW2": dLdW2,
"dLdb2": dLdb2}
return gradients, L许多人总是认为反向传播很困难,但是正如本文中介绍的情形,事实并非如此。必须掌握每个步骤,才能掌握整个反向传播技术。另外,有必要掌握线性代数和微积分等数学知识,以了解如何计算每个函数的各个梯度。使用这些工具,反向传播应该是小菜一碟!实际上,反向传播通常由使用的深度学习框架来处理。但是,了解这种技术的内在作用是值得的,因为它有时可以帮助我们理解神经网络为何训练得不好。
本文转载 小白遇见AI ,作者:小烦

















