湾区大神Beren Millidge：整数tokenization是疯狂的！ 原创

在与语言模型花费了很多时间后，我得出结论，总的来说，tokenization普遍来说是疯狂的，语言模型能学到任何东西都是一个奇迹。为了深入探讨最近一直困扰我的一个愚蠢的例子，让我们看一下GPT2分词器（据我所知，GPT3也使用相同的分词器）是如何对整数进行tokenization的。整数的tokenization是学习和表示数学事实的最基本要素，最终，所有GPT的数学能力都必须建立在这个基础上。

主要问题在于，这个分词器没有以十进制或者任何连贯的格式来表示数字。理想的十进制系统应该为整数0到9分配唯一的token，然后将更大的整数表示为这些唯一token的组合。十进制系统（实际上，以任何连贯的基数来表示整数）允许定义加法、减法、乘法等直接算法。

然而，GPT2分词器没有这样做，事实上，它没有以任何连贯的基数来表示整数。十进制数0到9是硬编码在其token集中的，以及其余的ASCII字符，但除此之外，BPE算法还将其他常见的数字块token化为唯一的token，并且并不总是以连贯的方式。相反，很多整数都被分配了自己独特的token。如下图所示：

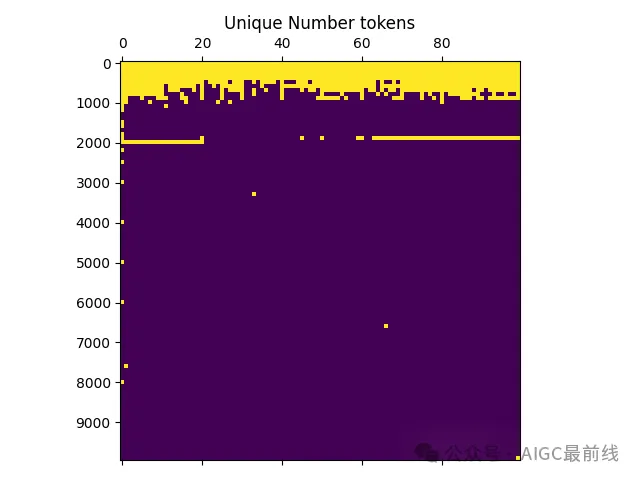
在GPT2分词器中前10000个整数的唯一token绘图。

每一行在这里代表100个整数，因此整个矩阵代表了从1到10000的前10000个整数。如果一个方格被涂成黄色，这意味着该整数被分配了一个唯一的token标识符，如果是蓝色，则该整数由一组组合的token编码。我们观察到，直到521为止的每一个整数都被分配了自己独特的token标识符，而且在此之后也有许多数字被分配了自己的独特标记。在前10000个整数中，有916个唯一的token（所以几乎有1/10的token是唯一的），数字token占总token空间的约1/50（GPT2的tokenizer大约有50k个token）。这意味着任何涉及这些整数的计算或数学问题必须以某种特殊方式处理，并且纯粹基于记忆运作。例如，当给出一个问题像54 + 72 = 126时，模型无法使用正常的加法算法，因为每一个token都是独一无二的。相反，它必须记忆大量的问题及其答案。基本上，几乎所有的两位数和大多数三位数的加减法问题都必须通过记忆而不是连贯和通用的算法来解决。

如果我们更仔细地检查这个图，我们会发现即使在前1000个数字之外，仍然有很多独特的数字。由于某种原因在训练集中常见的许多可识别的数字被分配了一个唯一的数字，这就需要学习专门的机制来处理涉及这些数字的任何计算。还有一个有趣的特征是在1900-2000区域分配了唯一token的整数带。这些代表了常见的日期 - 即从1930年到2020年的日期都分配了唯一的token，因为这些日期在训练集中出现的频率最高（有趣的是，唯一的token被分配到了2020年，然后突然停止，这使得您可以将tokenizer的创建日期定位在2019年至2020年）。

tokenization的荒谬之处也不仅仅限于许多唯一的token，还包括非唯一的整数是如何被token化的。对于这些数字，模型肯定不会采用连贯的十进制系统。相反，它将整数分成块，然后以临时的方式对它们进行token化。整数被分成块的方式甚至可以在相邻的数字之间变化。例如，数字2249被token化为“2”和“249”（1-3）。数字2250被token化为“22”和“50”（2-2），而数字“2251”则被token化为“225”和“1”（3-1）。

如果我们重复我们的分析，但为4位数如何被token化的不同类别着色 - 即作为唯一的、1-3长度的token、2-2 token或3-1 token，我们得到以下结果。

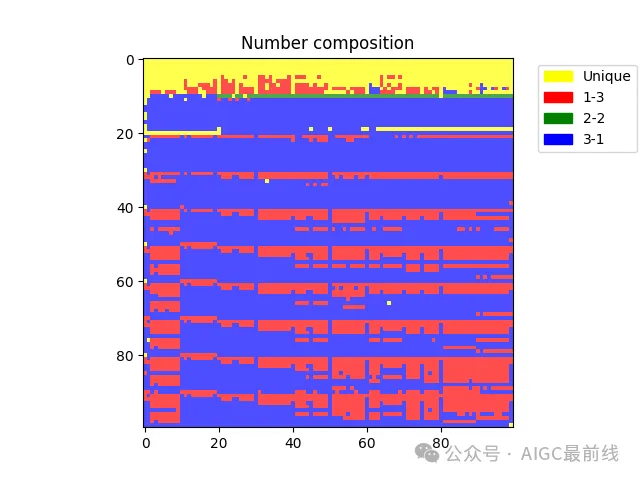
在 GPT2 分词器中复合数字 token 的构成图。

这里明显存在不随机的不同编码策略分布，每1000行都有一种略有重复的编码模式。但如果你仔细观察，你会发现其具体细节相当不一致。最终，这意味着即使是执行简单的数值算法，比如多位数的加法，模型也必须根据tokenization的具体细节学习一系列特殊情况，从观察更大数字的tokenization来看，这个问题似乎永远也解决不了，总会有大数字被不一致地分割成token和偶尔出现的独特token要处理。作为一个语言模型，真是太难了！

译自：https://www.beren.io/2023-02-04-Integer-tokenization-is-insane

谁是Beren Millidge？

Beren Millidge是旧金山湾区一家初创公司的联合创始人。在此之前，Beren花了一段时间共同创立了 Apollo Research，之前Beren曾担任 Conjecture 的研究主管。Beren曾在牛津大学从事计算神经科学的博士后研究，与 Rafal Bogacz 合作。Beren在爱丁堡大学完成了机器学习和计算神经科学的博士学位，并在苏塞克斯大学作为访问学者与 Alexander Tschantz、Chistopher Buckley 和 Anil Seth 合作。

本文转载自公众号AIGC最前线   

原文链接：​​https://mp.weixin.qq.com/s/mny12p1XKzIeCUGaMgg3fA​​