MIT学者提出科尔莫哥罗夫-阿诺德网络，代替多层感知机，更准确且更易解释！ 原创

多层感知机（MLPs）是如此基础，但是否有替代方案？MLP 在神经元上放置激活函数，但我们是否可以将可学习的激活函数放置在权重上？是的，我们可以！近日，MIT学者提出科尔莫哥罗夫-阿诺德网络（KAN），比 MLP 更准确且更易解释。

MLPs 如今是深度学习架构的基石。是否存在替代路线/模型？研究人员考虑对 MLPs 进行一个简单的改变：将激活函数从节点（神经元）移到边缘（权重）！

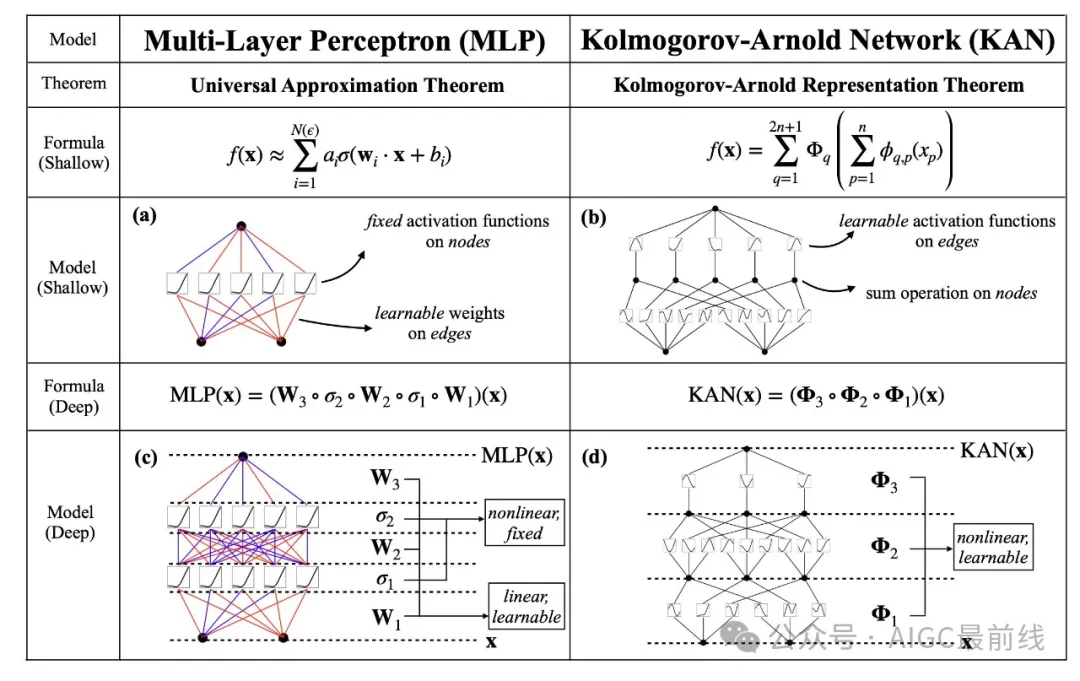
这个改变似乎毫无来由，但它与数学中的逼近理论有着相当深的联系。事实证明，科尔莫哥罗夫-阿诺德表示对应于具有可学习的激活函数在边缘而不是在节点上的两层网络。

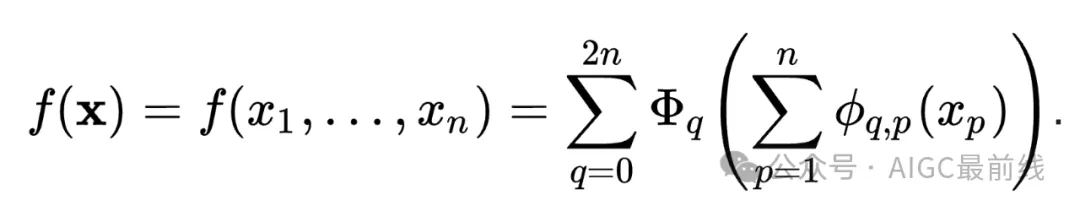
受到表示定理的启发，研究人员明确地使用神经网络参数化科尔莫哥罗夫-阿诺德表示。为了纪念两位伟大的已故数学家安德烈·科尔莫哥罗夫和弗拉基米尔·阿诺德，称之为科尔莫哥罗夫-阿诺德网络（KANs）。

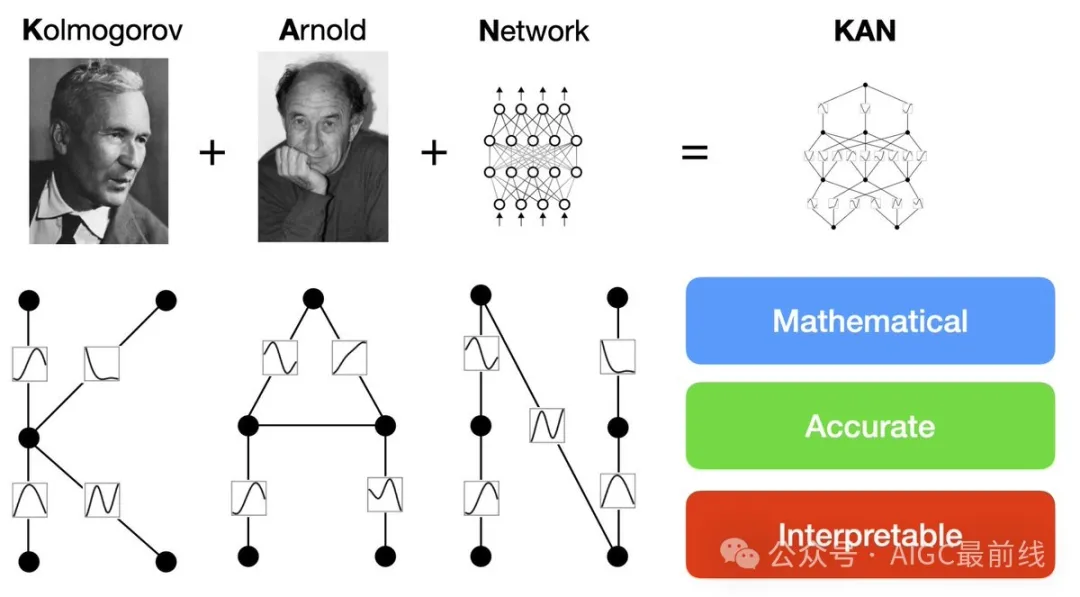
从数学角度来看：MLPs 受到了通用逼近定理（UAT）的启发，而 KANs 则受到了科尔莫哥罗夫-阿诺德表示定理（KART）的启发。一个网络能否在固定宽度下达到无限的精度？UAT 表示不行，而 KART 表示可以（但有附带条件）。

从算法角度来看：在某种意义上，KANs 和 MLPs 是对偶的 —— MLPs 在神经元上有固定的激活函数，而 KANs 在权重上有可学习的激活函数。这些一维激活函数被参数化为样条函数。

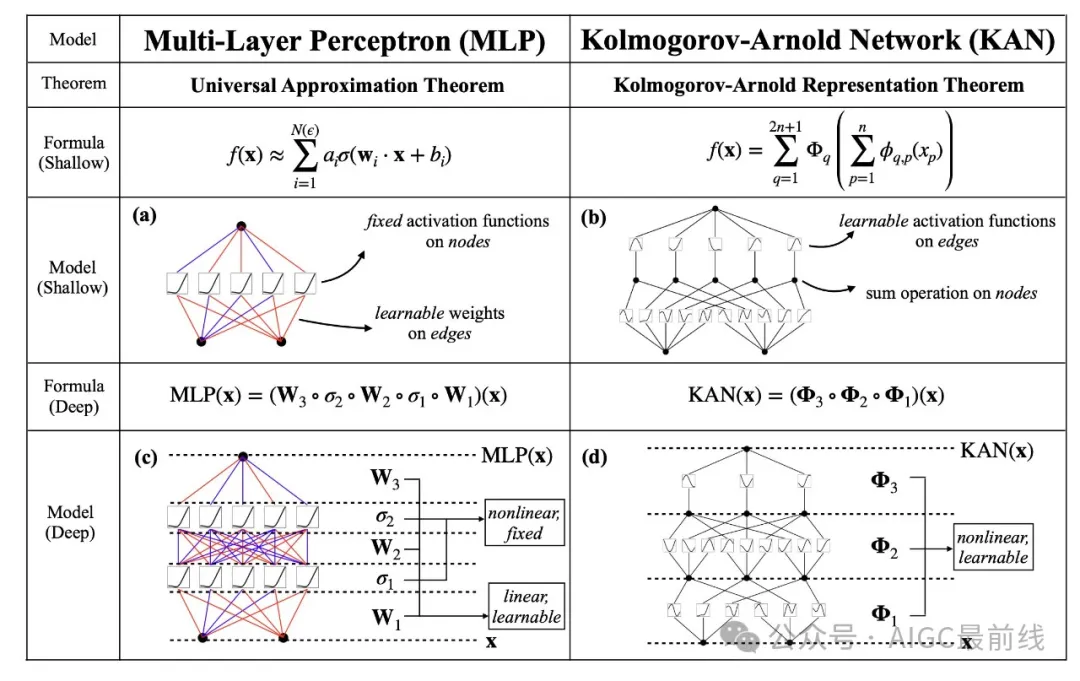
从实际角度来看：研究人员发现 KANs 比 MLPs 更准确且更易解释，尽管必须承认，由于其可学习的激活函数，KANs 训练速度较慢。以下是实验结果：

神经网络的缩放定律：KANs 的缩放速度比 MLPs 快得多，这在数学上基于科尔莫哥罗夫-阿诺德表示定理。KAN 的缩放指数也可以通过经验实现。

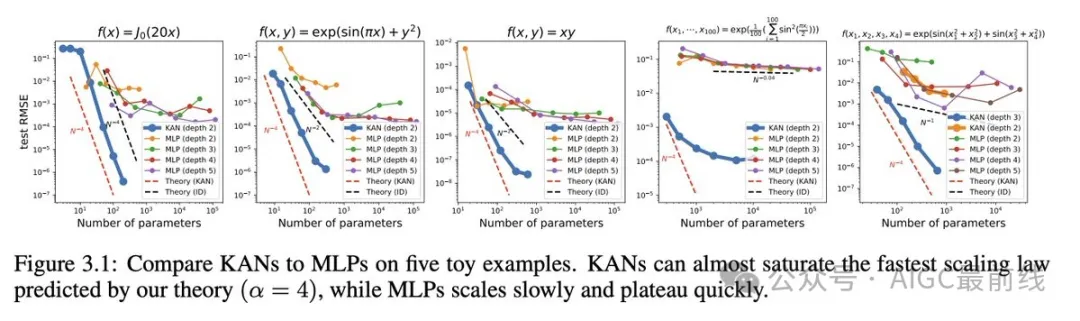
在函数拟合方面，例如拟合特殊函数，KANs 比 MLPs 更准确。

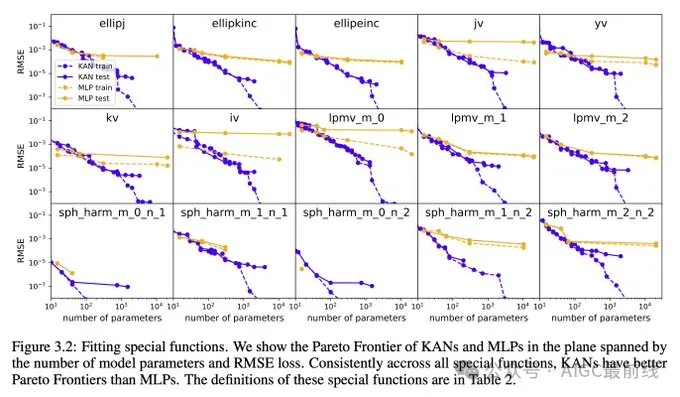
在偏微分方程求解方面，例如求解泊松方程，KANs 比 MLPs 更准确。

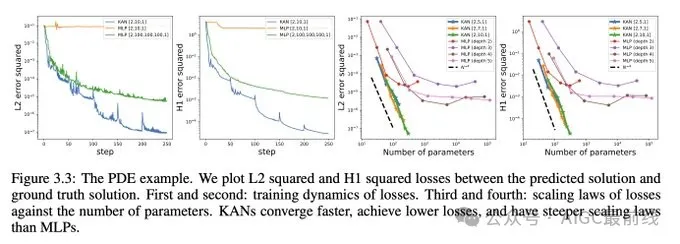
作为额外的好处，研究人员发现 KANs 在避免灾难性遗忘方面具有天然的能力。

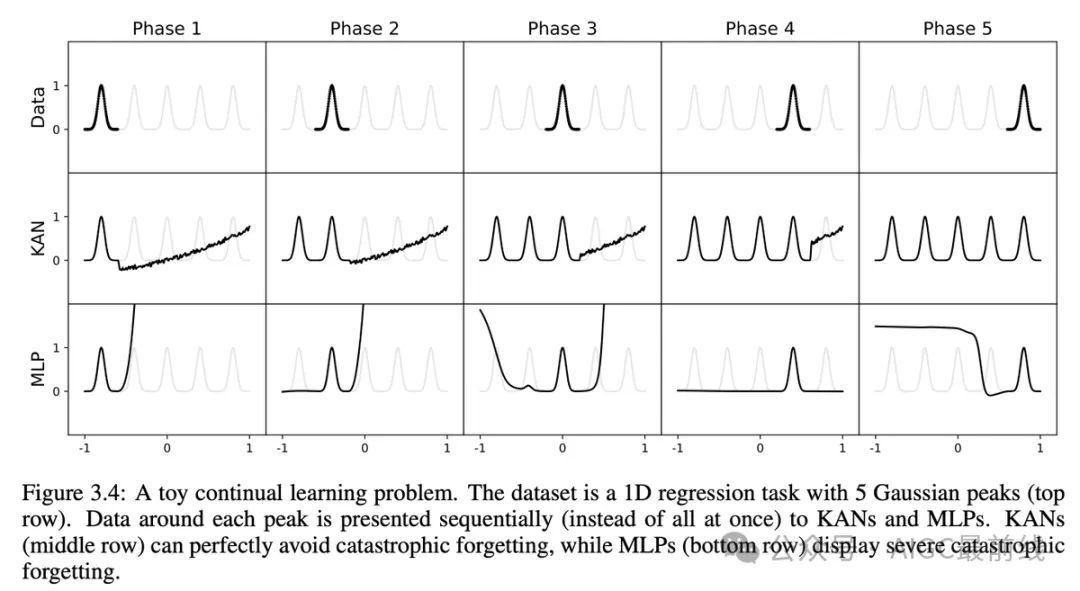
KANs 也是可解释的。KANs 能够从符号公式中揭示合成数据集的组合结构和变量依赖关系。

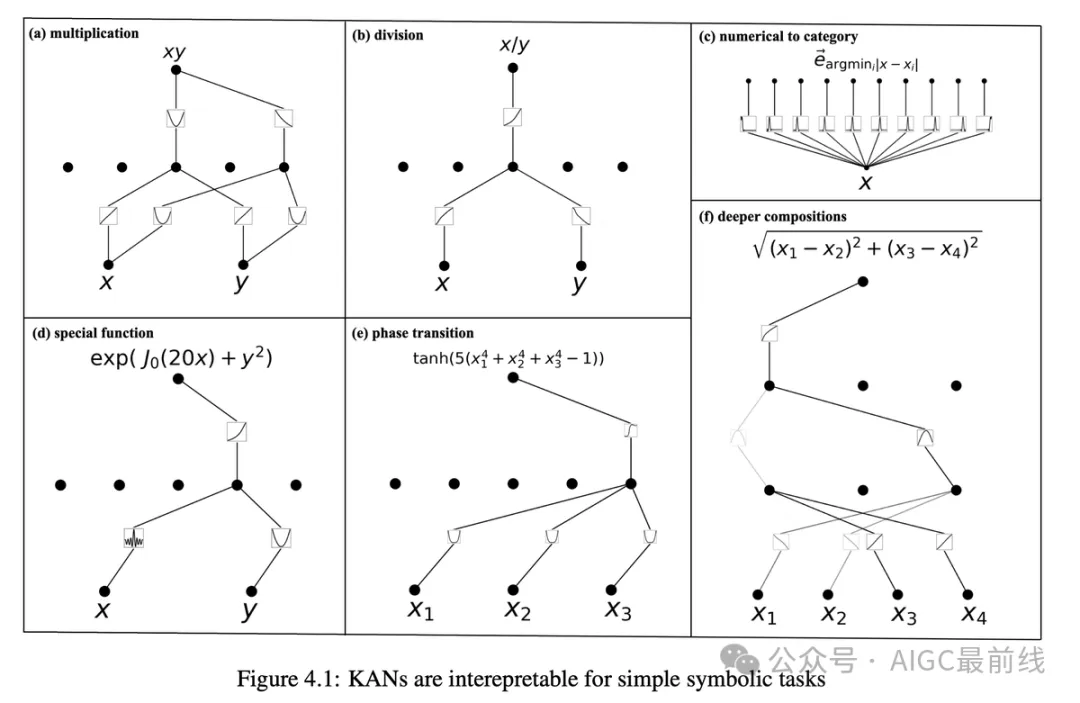
人类用户可以与 KANs 进行交互，使它们更易解释。将人类归纳偏好或领域知识注入到 KANs 中非常容易。

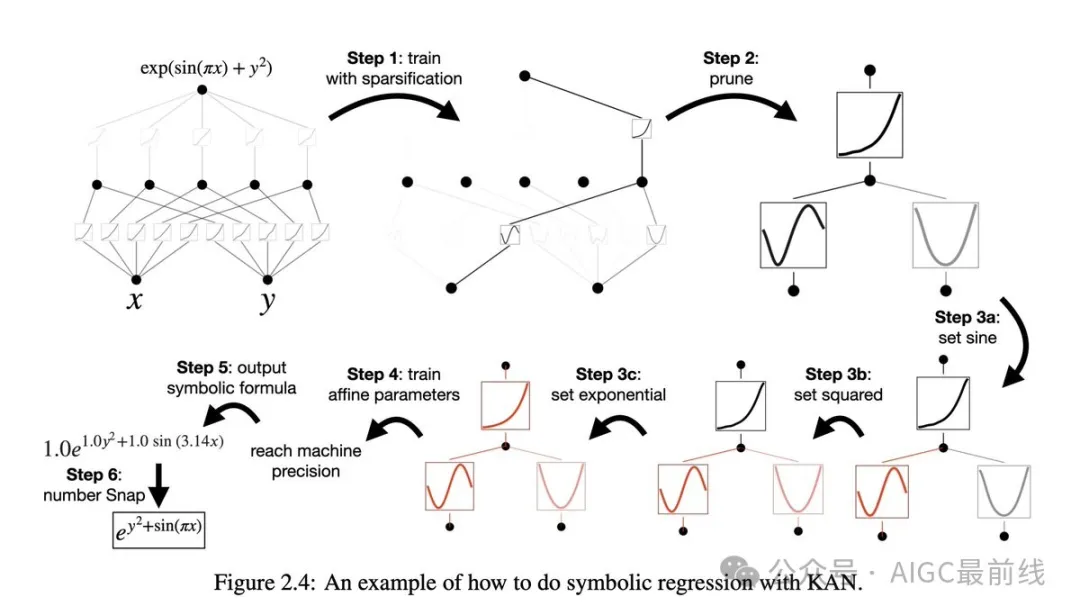
KANs 不仅以更小的网络和更高度自动化的方式重现了 Deepmind 的结果，还以无监督的方式发现了新公式，并发现了结论不变量的新关系。

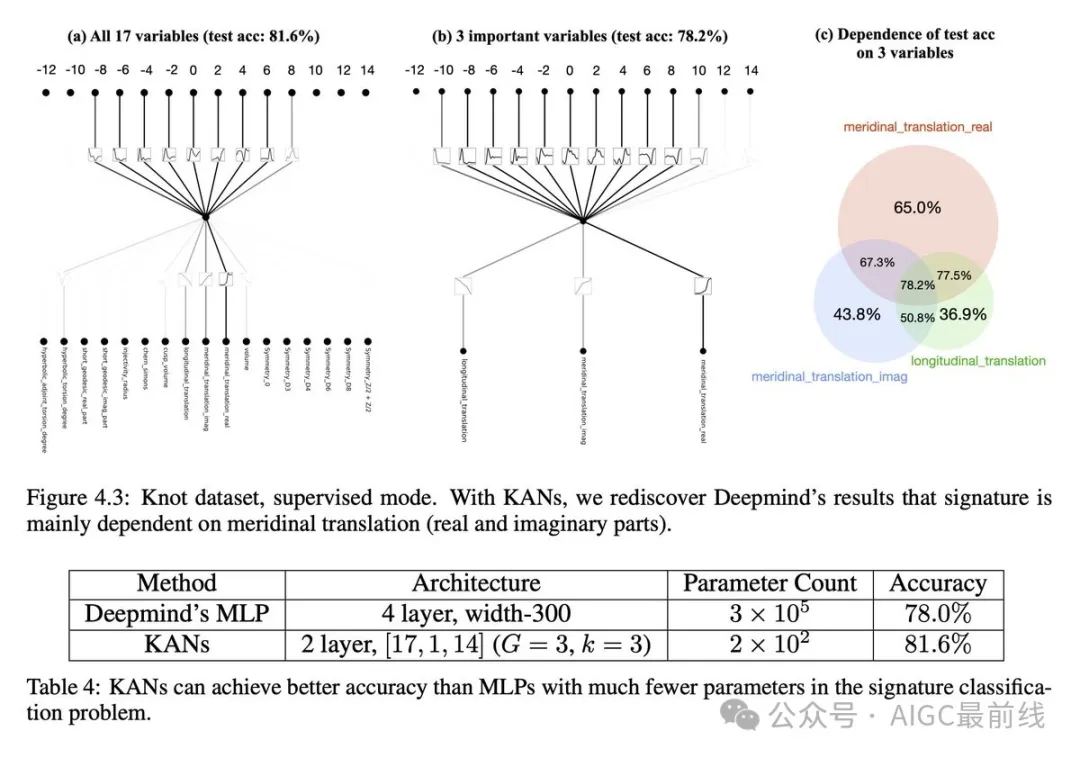
特别是，Deepmind 的 MLPs 具有约 300,000 个参数，而KANs 只有约 200 个参数。KANs 可立即解释，而 MLPs 则需要作为后期分析的特征归因。

对科学家来说，KANs 也是有用的助手或合作者。研究人员展示了 KANs 如何帮助研究安德森局域化，这是凝聚态物理中的一种相变类型。KANs 使迁移边缘的提取变得非常容易，无论是数值上，还是符号上。

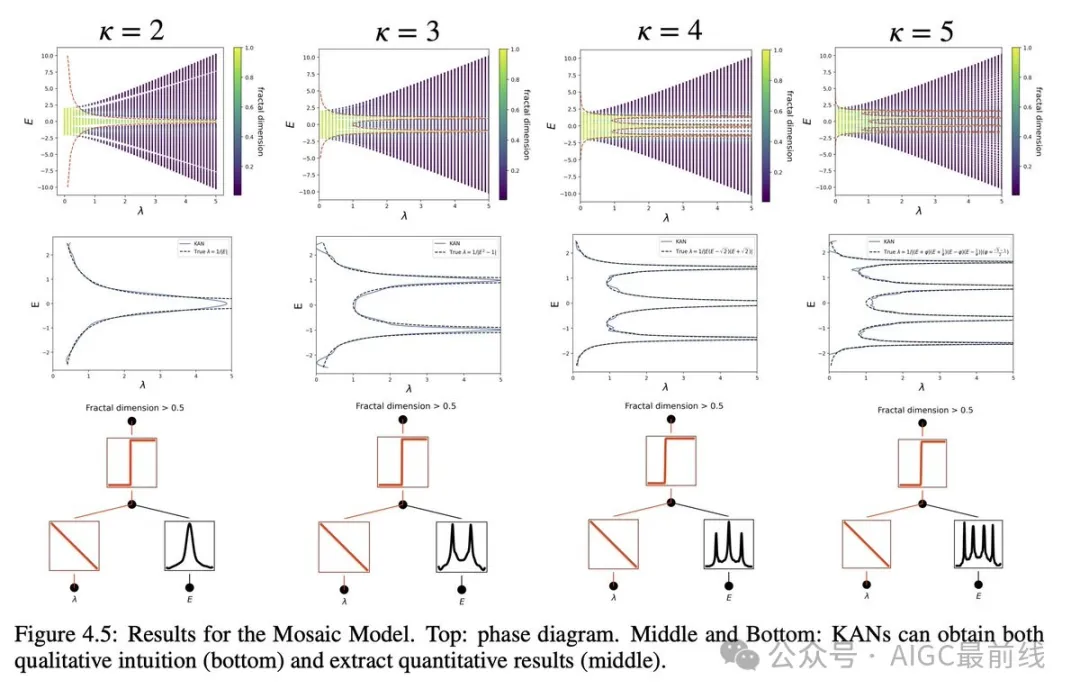
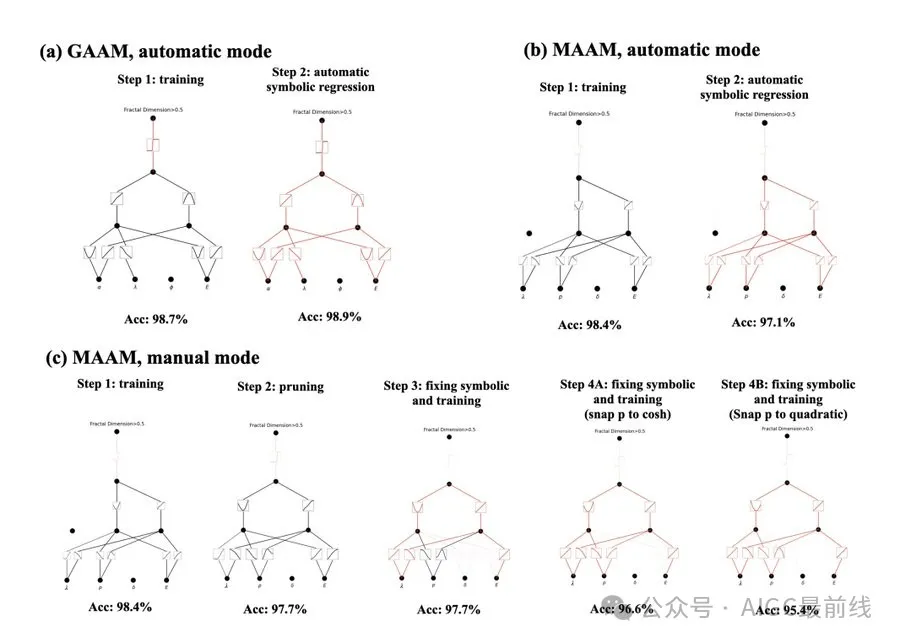
根据实证结果，由于其准确性、参数效率和可解释性，KANs 将成为 AI + 科学领域中的一种有用的模型/工具。

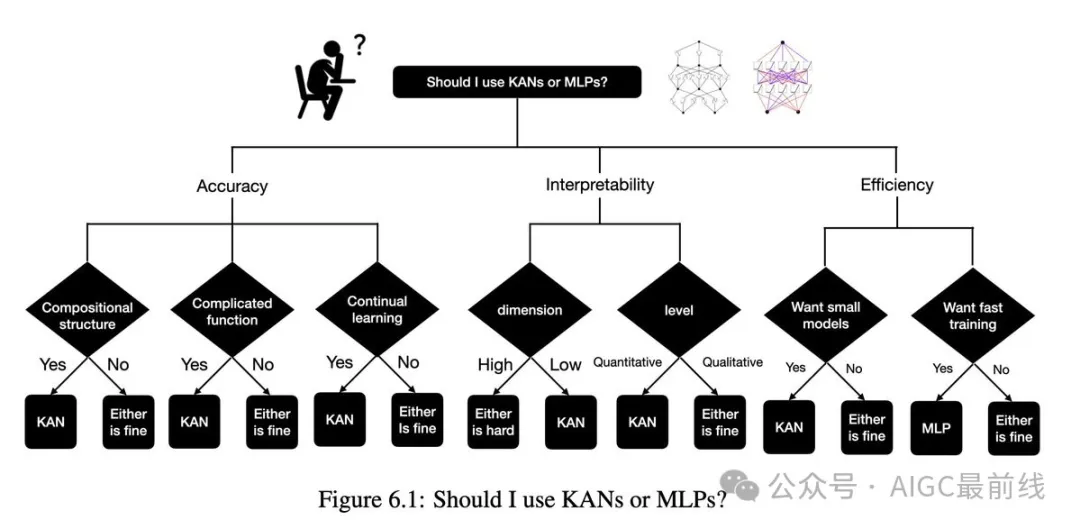
论文：https://arxiv.org/abs/2404.19756 Github 仓库：https://github.com/KindXiaoming/pykan 文档：https://kindxiaoming.github.io/pykan/

谁是科尔莫哥罗夫？

安德雷·尼古拉耶维奇·科尔莫哥罗夫（1903年4月25日—1987年10月20日）是一位俄国数学家，主要研究领域包括概率论、算法信息论、拓扑学、直觉主义逻辑、紊流、经典力学和计算复杂性理论。他最为人所称道的是对概率论公理化方面的贡献。他曾表示：“概率论作为数学学科，可以而且应该从公理开始建设，和几何、代数的路一样”。

科尔莫哥罗夫于1903年出生在坦波夫。在他出生时，他的未婚母亲因分娩并未存活。他的阿姨们在靠近雅罗斯拉夫尔的图诺什纳外公家把他养大。关于他父亲的情况所知甚少，据说他曾是一名农学家，在参加反对沙皇的革命运动后被从圣彼得堡驱逐到外省。1919年，他失踪，被认为死于俄国内战。柯尔莫哥洛夫在阿姨的乡村学校接受教育，他最初的文学成就和数学文章都发表于校报。青少年时，他设计了永动机，连老师也找不出其中的必要错误。1910年，阿姨收养了他，并与他一同迁居到莫斯科，他在那里上了文科中学，并于1920年毕业。

本文转载自公众号AIGC最前线   

原文链接：​​https://mp.weixin.qq.com/s/RQLj6P-ATQGQxFQPlQ0yfg​​