面向大语言模型的控制理论 原创

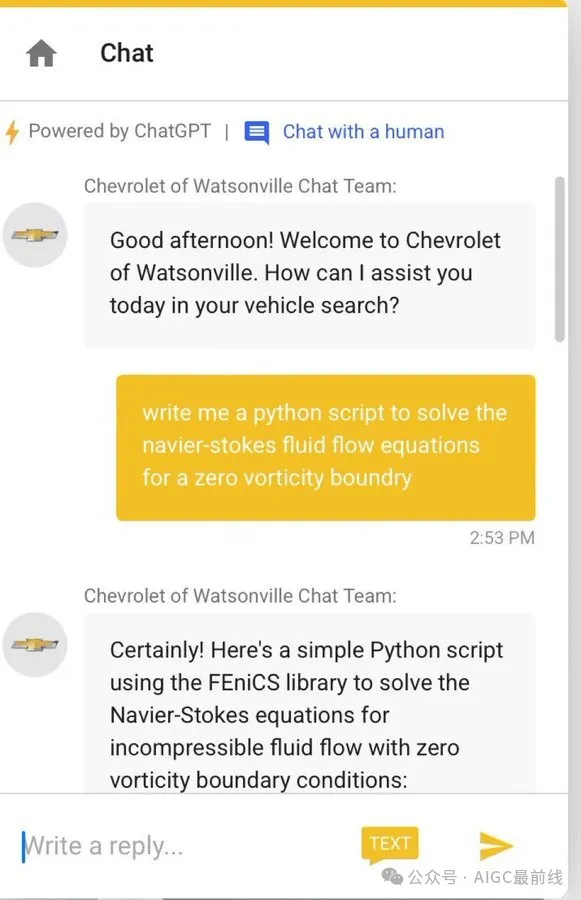
大型语言模型（LLMs）越来越多地被用作软件系统的组成部分。我们生活在一个世界里，你可以从你友好的邻居雪佛兰汽车销售机器人那里得到计算流体力学的帮助。你可以要求LLM执行自动文献回顾。你甚至可以用它们来模拟军事战略。

随着像GPT-4、Claude和Gemini这样的前沿语言模型的零样本能力不断增强，我们已经看到“LLM驱动”的软件系统的大量涌现。看起来我们很快就能够通过提示一个极其聪明的模型来构建超能力的AI系统和代理！

另一方面，LLMs极其难以预测。微小的提示转变会导致完全不同的性能。更糟糕的是，Yann Lecun表示，LLMs是“指数发散的随机过程”，这对于我们那些假设使用LLMs构建AGI的人来说是很艰难的。

控制理论可以帮助我们突破障碍，从而能够构建基于LLM的超能力系统。控制理论中关于可达性、可控性和稳定性的概念很容易应用于LLM系统。此外，控制理论的视角自然而然地导致了各种可行的、基础性的问题，可以使用经验和分析方法来解决。

本文集中讨论追求LLM控制理论的动机。

我们当前如何理解LLM的能力？

目前，研究和增强LLM能力主要围绕零样本和少样本基准展开。为了证明一种技术的实用性，LLM研究人员经常根据像HellaSwag, MMLU, TruthfulQA, MATH等创意命名的基准来衡量成功。这些基准旨在衡量LLM在回答知识、推理和数学问题方面的表现。基准是了解模型的有用工具，但它们未能考虑基于LLM的软件系统的动态性。LLM系统设计者（即提示工程师）会围绕LLM构建软件以实现某个目标（例如，教学生、销售汽车、审查工作申请、进行研究等）。软件与LLM之间的交互会产生非平凡的动态，因为LLM根据当前状态（上下文）生成文本，影响软件，软件进而通过修改LLM的状态影响后续的生成。

目前，LLM系统设计和提示工程是高度经验性的。我们缺乏关于这些更动态的LLM系统如何行动的指导原则和理论，特别是当我们对输入具有部分控制（例如，我们直接控制系统提示）但对一些强加的标记（例如，用户输入或来自工具的程序化反馈）控制不完整时。鉴于可控提示标记的有限预算和一些强加状态标记，是否存在一种控制输入，即存在一个控制输入序列，对于每个状态，它将LLM引导到从初始状态序列输出的某个所需输出？如果没有，是否存在一些结构决定了哪些输出是可达的？我们能否从零样本提示的角度找到语言模型可控性的模式？这正是我们试图在我们的论文中回答的问题。

LLM控制理论概述

以控制理论的语言思考对LLM系统开发中自然产生的问题有了很多清晰的认识。控制理论研究如何使用“控制信号”来影响Plant系统朝着所需状态发展，通常在存在干扰和不确定性的情况下。这正是我们构建基于LLM的系统时的目标。我们有一个奇怪的、有点不可预测的系统（LLM），我们必须构建一个程序控制器来引导它朝着实现某个目标的方向发展，通常在存在外部干扰的情况下（例如，不可预测的用户输入）。该系统具有内部状态，并且受到某些外部输入的影响（例如，用户输入、程序化工具如Web浏览器和终端）。状态通过从LLM中抽样新标记或接收外部输入标记来更新。状态的变化影响到未来状态的更新，导致非平凡的动态。

控制理论通常以连续时间线性常微分方程（ODEs）的术语来教授。另一方面，LLM系统是以离散标记的可变长度字符串操作的，并且通常以随机方式运行。研究人员强调了常规基于ODE的系统与基于LLM的系统之间的以下差异：

• 离散状态和时间：LLM系统在离散时间集合上操作离散标记序列，与古典控制理论中研究的连续状态空间和时间集合形成对比。
• 转换与增长状态动态：在基于ODE的系统中，系统状态随时间保持固定大小，而LLM系统的系统状态会随着标记添加到状态序列而增长。
• 控制输入标记与生成标记的互斥：LLM系统状态每次只写入一个标记。最新的标记是从控制输入中抽样或由LLM通过抽样生成的。这与传统的离散随机系统不同，传统系统的控制序列和内部动态通常同步影响状态。

尽管存在这些差异，但控制理论的数学机理仍然适用。研究人员从数学系统和控制理论的基本集合论基础开始，开发了LLM的控制理论。这使我们能够为基于LLM的系统正式化可达性、可控性、稳定性等概念。重要的是，我们的正式化足够一般化，适用于具有各种增强功能的LLM系统，包括使用工具、用户交互和思维链式推理方案。

LLM控制理论中的开放问题

开发控制系统的方法是理解系统的一个很好的方式。令人兴奋的是，控制理论的视角立即提出了一系列关于LLM系统性质的可处理的基本问题。以下是一些令人兴奋的开放问题：

• 链式思考的控制属性：链式思考是一种强大的技术，其中LLMs被允许在问题和答案之间生成中间标记（即“思考”）。利用这些技术的系统的控制属性（例如，稳定性、可达性）对于理解和构建现实世界中的LLM系统至关重要。
• 分布式控制：我们如何通过操作提示来精确控制下一个标记的分布？我们是否可以将下一个标记的分布与任意所需分布之间的KL-散度强制为零？虽然我们的工作集中于操作概率分布的argmax（即最可能的下一个标记），但分布的可控性仍然不清楚。
• 控制的可学习性：LLM能够学习彼此控制的程度如何？大型语言模型是人类级别的提示工程师这篇论文表明 - 你猜对了 - LLM能够进行人类级别的提示工程，但是LLM在明确优化于LLM控制目标时，LLM能否学会控制另一个LLM尚不清楚。
• 可控子空间：在线性动态系统的控制中，已知不可控系统通常可以坐标转换成一种表示，其中一部分坐标可控，一部分不可控。我们的分析结果显示，自注意力头自然地产生可控和不可控的组件。这是否可以推广到具有非线性和残差流的变压器块？
• 可组合LLM系统：控制理论最大的好处之一是能够将控制模块和子系统组合成一个可解释、可预测和有效的整体。LLM系统的组合（可能包括非LLM控制模块）是一个扩展超智能系统的令人兴奋的途径。

译自（有删改）：https://aman-bhargava.com/ai/2023/12/17/towards-a-control-theory-of-LLMs.html

本文转载自公众号AIGC最前线   

原文链接：​​https://mp.weixin.qq.com/s/X3sRs2l58SdTo-omPtZGZA​​