回复
深度解析理解 Transformer 中的3大位置嵌入：从绝对位置嵌入到旋转位置嵌入 精华
Transformer的关键组件之一是位置嵌入。你可能会问：为什么呢？因为Transformer中的自注意力机制是排列不变的；这意味着它计算输入中每个标记从序列中其他标记接收的注意力程度，但它没有考虑标记的顺序。实际上，注意力机制将序列视为一个标记集合。因此，我们需要另一个称为位置嵌入的组件，它可以考虑标记的顺序，并对标记嵌入产生影响。
但是，位置嵌入有哪些不同类型，它们又是如何实现的呢？
在本文中，我们将研究三种主要的位置嵌入类型：绝对位置嵌入、相对位置嵌入和旋转位置嵌入（RoPE），并深入探讨它们的实现方式。
1. 背景
在自然语言处理（NLP）中，序列中单词的顺序对于理解语义非常重要，这对人类来说也是如此。如果顺序混乱，语义就会完全改变。例如“Sam sits down on the mat”（山姆坐在垫子上）和“The mat sits down on Sam”（垫子坐在山姆身上），仅仅重新排列单词顺序，语义就完全不同了。
Transformer是许多现代NLP系统的核心，它并行处理所有单词。这种并行处理发生在注意力机制中，在该机制中，模型计算每个标记从输入上下文中其他标记接收的注意力分数。虽然并行处理本质上有利于提高效率，但它导致模型丢失了所有关于单词顺序的信息。因此，Transformer有一个额外的组件，即位置嵌入，它创建包含序列中标记位置或顺序信息的向量。
位置嵌入有很多不同类型。三种主要的、广为人知的类型是绝对位置嵌入、相对位置嵌入和旋转位置嵌入（RoPE）。
2. 绝对位置嵌入
绝对位置嵌入就像是给句子中的每个标记分配一个唯一的编号。在实际操作中，我们为序列中的每个位置创建一个向量。在最简单的情况下，每个标记的位置嵌入是一个独热向量，除了标记所在位置的索引处为1，其他位置均为0。然后，在将标记嵌入输入到Transformer之前，我们将这些位置嵌入向量添加到标记嵌入中。
例如，在句子“I am a student”（我是一名学生）中，有4个标记。每个标记都有一个唯一的位置嵌入向量。假设嵌入维度为3，那么第一个标记“I”将得到独热编码[1, 0, 0]，第二个标记“am”将得到[0, 1, 0]，依此类推。
虽然独热编码是传达位置嵌入概念的一种直接方法，但在实际中，有更好的方法来实现绝对位置嵌入。所有不同的实现方式都既简单又有效，但它们在处理非常长的序列或比训练时更长的序列时可能会遇到困难。
让我们来看看这些实现方式。
2.1 实现方式
绝对位置嵌入的实现通常涉及创建一个大小为_vocabulary * embeddingdim_的查找表。这意味着词汇表中的每个标记在查找表中都有一个条目，并且该条目的维度为_embeddingdim_。
绝对位置嵌入主要有两种类型：
- 学习型：在学习型方法中，嵌入向量在训练过程中随机初始化，然后进行训练。原始的Transformer论文[5]以及像BERT、GPT和RoBERTa等流行模型都采用了这种方法。很快，我们将在代码中看到这种方法的示例。这种方法的一个缺点是，它可能无法很好地泛化到比训练时更长的序列，因为对于那些位置，查找表中不存在相应的条目。
- 固定型：这种方法也称为正弦位置编码，在开创性的“Attention Is All You Need”论文[5]中被提出。该方法使用不同频率的正弦和余弦函数为每个位置创建独特的模式。这种编码的公式如下：
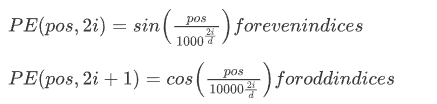
在上述公式中，是位置嵌入，是模型的维度，也称为嵌入维度。基本上，位置为的位置嵌入向量，在偶数索引处由函数决定，在奇数索引处由函数决定。
这种方法的一个关键优点是它能够外推到训练期间未遇到的序列长度；这在处理不同的输入大小方面提供了很大的灵活性。
无论采用哪种类型（学习型或固定型），一旦创建了绝对位置嵌入，就会将它们添加到标记嵌入中：
Final Embedding = Token Embedding + Positional Embedding
让我们一起从RoBERTa模型的源代码中查看学习型位置嵌入。代码取自HuggingFace代码库。
class RobertaEmbeddings(nn.Module):
# Copied from transformers.models.bert.modeling_bert.BertEmbeddings.__init__
def __init__(self, config):
super().__init__()
self.word_embeddings = nn.Embedding(config.vocab_size, config.hidden_size, padding_idx=config.pad_token_id)
self.position_embeddings = nn.Embedding(config.max_position_embeddings, config.hidden_size)
self.token_type_embeddings = nn.Embedding(config.type_vocab_size, config.hidden_size)
# self.LayerNorm is not snake-cased to stick with TensorFlow model variable name and be able to load
# any TensorFlow checkpoint file
self.LayerNorm = nn.LayerNorm(config.hidden_size, eps=config.layer_norm_eps)
self.dropout = nn.Dropout(config.hidden_dropout_prob)
# position_ids (1, len position emb) is contiguous in memory and exported when serialized
self.position_embedding_type = getattr(config, "position_embedding_type", "absolute")
self.register_buffer(
"position_ids", torch.arange(config.max_position_embeddings).expand((1, -1)), persistent=False
)
self.register_buffer(
"token_type_ids", torch.zeros(self.position_ids.size(), dtype=torch.long), persistent=False
)
# End copy
self.padding_idx = config.pad_token_id
self.position_embeddings = nn.Embedding(
config.max_position_embeddings, config.hidden_size, padding_idx=self.padding_idx
)
def forward(
self, input_ids=None, token_type_ids=None, position_ids=None, inputs_embeds=None, past_key_values_length=0
):
if position_ids isNone:
if input_ids isnotNone:
# Create the position ids from the input token ids. Any padded tokens remain padded.
position_ids = create_position_ids_from_input_ids(input_ids, self.padding_idx, past_key_values_length)
else:
position_ids = self.create_position_ids_from_inputs_embeds(inputs_embeds)
if input_ids isnotNone:
input_shape = input_ids.size()
else:
input_shape = inputs_embeds.size()[:-1]
seq_length = input_shape[1]
# Setting the token_type_ids to the registered buffer in constructor where it is all zeros, which usually occurs
# when its auto-generated, registered buffer helps users when tracing the model without passing token_type_ids, solves
# issue #5664
if token_type_ids isNone:
if hasattr(self, "token_type_ids"):
buffered_token_type_ids = self.token_type_ids[:, :seq_length]
buffered_token_type_ids_expanded = buffered_token_type_ids.expand(input_shape[0], seq_length)
token_type_ids = buffered_token_type_ids_expanded
else:
token_type_ids = torch.zeros(input_shape, dtype=torch.long, device=self.position_ids.device)
if inputs_embeds isNone:
inputs_embeds = self.word_embeddings(input_ids)
token_type_embeddings = self.token_type_embeddings(token_type_ids)
embeddings = inputs_embeds + token_type_embeddings
if self.position_embedding_type == "absolute":
position_embeddings = self.position_embeddings(position_ids)
embeddings += position_embeddings
embeddings = self.LayerNorm(embeddings)
embeddings = self.dropout(embeddings)
return embeddings注意在__init__方法中，以下这行代码是如何用随机值初始化学习型位置嵌入的：
self.position_embeddings = nn.Embedding(config.max_position_embeddings, config.hidden_size)然后在forward方法中，将位置嵌入添加到标记嵌入中：
if self.position_embedding_type == "absolute":
position_embeddings = self.position_embeddings(position_ids)
embeddings += position_embeddings让我们在文本输入上一起运行这段代码，看看结果：
from transformers import RobertaConfig
config = RobertaConfig()
print(config)输出：
RobertaConfig {
"attention_probs_dropout_prob": 0.1,
"bos_token_id": 0,
"classifier_dropout": null,
"eos_token_id": 2,
"hidden_act": "gelu",
"hidden_dropout_prob": 0.1,
"hidden_size": 768,
"initializer_range": 0.02,
"intermediate_size": 3072,
"layer_norm_eps": 1e-12,
"max_position_embeddings": 512,
"model_type": "roberta",
"num_attention_heads": 12,
"num_hidden_layers": 12,
"pad_token_id": 1,
"position_embedding_type": "absolute",
"transformers_version": "4.31.0",
"type_vocab_size": 2,
"use_cache": true,
"vocab_size": 50265
}正如你在上面打印的配置参数中看到的，我们有"position_embedding_type": "absolute"，并且上下文窗口长度为512："max_position_embeddings": 512。让我们获取一个RobertaEmbedding对象：
emb = RobertaEmbeddings(config)
print(emb)输出：
RobertaEmbeddings(
(word_embeddings): Embedding(50265, 768, padding_idx=1)
(position_embeddings): Embedding(512, 768, padding_idx=1)
(token_type_embeddings): Embedding(2, 768)
(LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)
(dropout): Dropout(p=0.1, inplace=False)
)你可以看到上面的RobertaEmbedding层，有一个(word_embeddings): Embedding(50265, 768, padding_idx=1)，这是一个随机初始化的嵌入矩阵，形状为50265*768；这意味着词汇表大小为50265，每个嵌入向量是768维的。
然后我们看到(position_embeddings): Embedding(512, 768, padding_idx=1)，这是位置嵌入向量，同样是随机初始化的，并且是768维向量。注意这个嵌入矩阵的大小是512*768，这表明我们只为512个位置提供位置嵌入。因此，如果在推理时出现长度超过512个标记的序列，我们将没有为其学习到的位置嵌入！！这就是我们前面讨论的学习型绝对位置嵌入的一个缺点。
让我们取一个序列并将其输入到嵌入层：
from transformers import RobertaTokenizer
# Initialize the tokenizer
tokenizer = RobertaTokenizer.from_pretrained("roberta-base")
sentence = "The quick brown fox jumps over the lazy dog."
# Tokenize the sentence
tokens = tokenizer.tokenize(sentence)
print(tokens)
# Get the input IDs
input_ids = tokenizer.encode(sentence, add_special_tokens=True)
print("\nInput IDs:", input_ids)输出：
['The', 'Ġquick', 'Ġbrown', 'Ġfox', 'Ġjumps', 'Ġover', 'Ġthe', 'Ġlazy', 'Ġdog', '.']
Input IDs: [0, 133, 2119, 6219, 23602, 13855, 81, 5, 22414, 2335, 4, 2]注意这个序列有12个标记。我们将其输入到嵌入层：
input_tensor = torch.tensor(input_ids).reshape((1,-1))
emb(input_ids=input_tensor)输出：
tensor([[[-0.7226, -2.3475, -0.5119, ..., -1.3224, -0.0000, -0.9497],
[-0.4094, 0.7778, 1.8330, ..., 0.1183, -0.3897, -1.8805],
[-0.7342, -1.6158, 0.2465, ..., -0.0000, -1.4895, -0.8259],
...,
[-0.2884, -3.0506, 0.6108, ..., 0.8692, 0.9901, 0.6638],
[ 0.6423, -2.1128, 1.2056, ..., 0.2799, 0.5368, -1.0147],
[-0.4305, -0.4462, -1.2317, ..., 0.4016, 1.8494, -0.2363]]],
grad_fn=<MulBackward0>)输出张量是从相应嵌入矩阵中检索到的标记嵌入和位置嵌入的总和。
3. 相对位置嵌入
相对位置嵌入关注序列中标记之间的距离关系，而不考虑标记的具体位置。
3.1 通俗解释
考虑句子“I am a student”（我是一名学生）。“I”的精确位置是1，“student”的精确位置是4。这些是标记的绝对位置。相对位置嵌入不考虑这些，它只考虑“I”与“student”的距离是3，与“am”的距离是1。
相对位置嵌入在处理较长序列时具有优势，并且对训练期间未见过的序列长度具有更好的泛化能力。我们很快就会看到原因。
一些使用相对位置嵌入的著名模型有Transformer-XL [1]、T5（文本到文本转移Transformer）[2]、DeBERTa（具有解耦注意力的解码增强BERT）[3]和带有相对位置嵌入的BERT [4]。你可以随意阅读这些论文，了解它们是如何实现相对位置嵌入的。
3.2 技术解释
首先，与将位置嵌入添加到标记嵌入的绝对位置嵌入不同，相对位置嵌入创建表示标记之间相对距离的矩阵。例如，如果标记i在位置2，标记j在位置5，相对位置就是j - i = 3。
然后，相对位置嵌入修改注意力分数，以包含关于相对位置的信息。如你所知，在自注意力机制中，注意力分数是在标记对之间计算的。因此，相对位置嵌入根据相对位置添加一个偏差项到注意力分数中，或者为每个可能的相对距离合并一个可学习的嵌入。
这种方法的一种常见实现是在注意力分数上添加一个相对位置偏差。如果A是注意力分数矩阵，添加一个相对位置偏差矩阵B：
3.3 代码示例：Transformer-XL的实现
下面是一个在PyTorch中实现相对位置嵌入的简单代码，该实现与Transformer-XL的实现方式相近。
import torch
import torch.nn as nn
class RelativePositionalEmbedding(nn.Module):
def __init__(self, max_len, d_model):
super(RelativePositionalEmbedding, self).__init__()
self.max_len = max_len
self.d_model = d_model
self.relative_embeddings = nn.Embedding(2 * max_len - 1, d_model)
def forward(self, seq_len):
# 生成相对位置
range_vec = torch.arange(seq_len)
range_mat = range_vec[None, :] - range_vec[:, None]
clipped_mat = torch.clamp(range_mat, -self.max_len + 1, self.max_len - 1)
relative_positions = clipped_mat + self.max_len - 1
return self.relative_embeddings(relative_positions)
class RelativeSelfAttention(nn.Module):
def __init__(self, d_model, num_heads, max_len):
super(RelativeSelfAttention, self).__init__()
self.num_heads = num_heads
self.d_k = d_model // num_heads
self.query = nn.Linear(d_model, d_model)
self.key = nn.Linear(d_model, d_model)
self.value = nn.Linear(d_model, d_model)
self.relative_pos_embedding = RelativePositionalEmbedding(max_len, d_model)
self.softmax = nn.Softmax(dim=-1)
def forward(self, x):
batch_size, seq_len, d_model = x.size()
Q = self.query(x).view(batch_size, seq_len, self.num_heads, self.d_k)
K = self.key(x).view(batch_size, seq_len, self.num_heads, self.d_k)
V = self.value(x).view(batch_size, seq_len, self.num_heads, self.d_k)
# 计算标准注意力分数
scores = torch.einsum('bnqd,bnkd->bnqk', Q, K) / (self.d_k ** 0.5)
# 获取相对位置嵌入
rel_pos_embeddings = self.relative_pos_embedding(seq_len)
rel_scores = torch.einsum('bnqd,rlkd->bnqk', Q, rel_pos_embeddings)
# 添加相对位置分数
scores += rel_scores
attn_weights = self.softmax(scores)
# 计算最终输出
output = torch.einsum('bnqk,bnvd->bnqd', attn_weights, V).contiguous()
output = output.view(batch_size, seq_len, d_model)
return output我们可以使用以下参数调用它：
seq_len = 10
d_model = 512
num_heads = 8
max_len = 20
x = torch.randn(32, seq_len, d_model) # 序列批次
attention = RelativeSelfAttention(d_model, num_heads, max_len)
output = attention(x)注意，seq_len（序列长度）指的是特定批次中输入序列的实际长度，每个批次的seq_len会有所不同。
然而，max_len（最大长度）是一个预定义的值，表示模型将考虑的最大相对位置距离。这个值决定了模型将为哪些相对位置学习嵌入。如果max_len设置为20，模型将为从 -19到19的相对位置学习嵌入。
请注意，这就是为什么self.relative_embeddings = nn.Embedding(2 * max_len - 1, d_model)设置为这个大小，以适应max_len定义范围内的所有可能相对位置。
现在，让我们解释一下代码：
第一个类如下，它为2 * max_len - 1的大小创建一个可学习的嵌入矩阵。在forward函数中，对于给定的序列，它从relative_embeddings矩阵中检索相应的嵌入。
class RelativePositionalEmbedding(nn.Module):
def __init__(self, max_len, d_model):
super(RelativePositionalEmbedding, self).__init__()
self.max_len = max_len
self.d_model = d_model
self.relative_embeddings = nn.Embedding(2 * max_len - 1, d_model)
def forward(self, seq_len):
# 生成相对位置
range_vec = torch.arange(seq_len)
range_mat = range_vec[None, :] - range_vec[:, None]
clipped_mat = torch.clamp(range_mat, -self.max_len + 1, self.max_len - 1)
relative_positions = clipped_mat + self.max_len - 1
return self.relative_embeddings(relative_positions)第二个类（如下）接收一个序列（即x），并计算查询、键和值矩阵。注意，每个注意力头都有自己的Q、K和V，这就是为什么所有这些矩阵的形状都是(batch_size, seq_len, self.num_heads, self.d_k)。
class RelativeSelfAttention(nn.Module):
def __init__(self, d_model, num_heads, max_len):
super(RelativeSelfAttention, self).__init__()
self.num_heads = num_heads
self.d_k = d_model // num_heads
self.query = nn.Linear(d_model, d_model)
self.key = nn.Linear(d_model, d_model)
self.value = nn.Linear(d_model, d_model)
self.relative_pos_embedding = RelativePositionalEmbedding(max_len, self.d_k)
self.softmax = nn.Softmax(dim=-1)
def forward(self, x):
batch_size, seq_len, d_model = x.size()
Q = self.query(x).view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)
K = self.key(x).view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)
V = self.value(x).view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)
# 计算标准注意力分数
scores = torch.einsum('bhqd,bhkd->bhqk', Q, K) / (self.d_k ** 0.5)
# 获取相对位置嵌入
rel_pos_embeddings = self.relative_pos_embedding(seq_len) # (seq_len, seq_len, d_k)
rel_pos_embeddings = rel_pos_embeddings.transpose(0, 2).transpose(1, 2) # (d_k, seq_len, seq_len)
rel_scores = torch.einsum('bhqd,dqk->bhqk', Q, rel_pos_embeddings)
# 添加相对位置分数
scores += rel_scores
attn_weights = self.softmax(scores)
# 计算最终输出
output = torch.einsum('bhqk,bhvd->bhqd', attn_weights, V).contiguous()
output = output.transpose(1, 2).reshape(batch_size, seq_len, d_model)
return output这行scores = torch.einsum('bhqd,bhkd->bhqk', Q, K) / (self.d_k ** 0.5)是一种强大的符号表示，用于简洁地指定复杂的张量运算。在这个上下文中，它用于计算查询向量和键向量之间的点积。'bhqd,bhkd->bhqk'这个公式可以解释如下：
-
b：批次大小。 -
h：注意力头的数量。 -
q：查询序列长度。 -
k：键序列长度（在自注意力中通常与查询序列长度相同）。 -
d：每个头的深度（即self.d_k）。
einsum符号'bhqd,bhkd->bhqk'指定在保持其他维度不变的情况下，计算Q和K的最后一个维度之间的点积。
下一行rel_pos_embeddings = self.relative_pos_embedding(seq_len)检索序列中所有现有相对距离的相对位置嵌入，这就是为什么它的形状是(seq_len, seq_len, d_k)。然后我们对其进行转置，将形状变为(d_k, seq_len, seq_len)。下一行rel_scores = torch.einsum('bhqd,dqk->bhqk', Q, rel_pos_embeddings)计算相对位置嵌入在自注意力机制中对注意力分数的贡献。这就是我们前面看到的公式中的相对位置偏差矩阵B。
最后，我们将矩阵B添加到原始注意力分数中：
# 添加相对位置分数
scores += rel_scores
attn_weights = self.softmax(scores)并与值矩阵V相乘得到输出：
# 计算最终输出
output = torch.einsum('bhqk,bhvd->bhqd', attn_weights, V).contiguous()
output = output.transpose(1, 2).reshape(batch_size, seq_len, d_model)
return output4. 旋转位置嵌入
旋转位置嵌入，通常称为RoPE（Rotary Position Embedding），是一种巧妙的方法，结合了绝对位置嵌入和相对位置嵌入的一些优点。这种方法在Roformer论文中被提出。
4.1 通俗解释
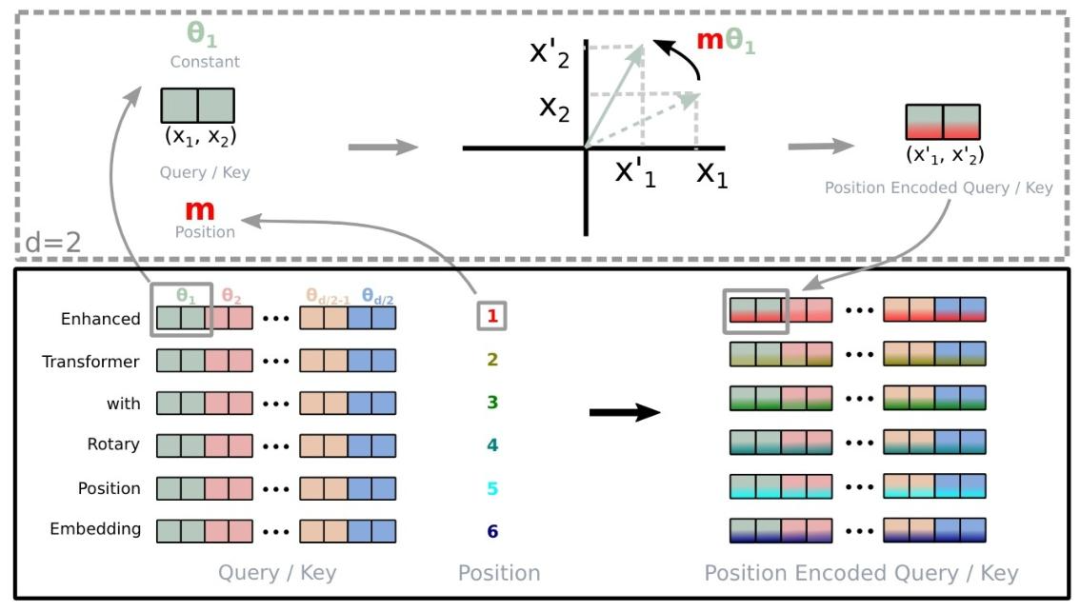
RoPE的核心思想是通过在高维空间中旋转词向量来编码位置信息。旋转的幅度取决于单词或标记在序列中的位置。
这种旋转具有一个很好的数学特性：任意两个单词之间的相对位置可以通过一个单词的向量相对于另一个单词的向量旋转了多少来轻松计算。因此，虽然每个单词根据其绝对位置获得唯一的旋转，但模型也可以很容易地确定相对位置。
RoPE有几个优点：它比绝对位置嵌入更有效地处理更长的序列。它自然地结合了绝对位置信息和相对位置信息。而且正如我们后面将看到的，它在计算上效率高且易于实现。
4.2 技术解释
给定一个标记嵌入和该标记的位置，绝对位置嵌入计算一个位置嵌入并将其添加到标记嵌入中：
然而，在旋转位置嵌入中，给定一个标记嵌入和它的位置，它会生成一个新的嵌入，其中包含位置信息：
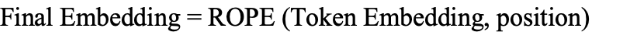
让我们看看这是如何计算的：
给定一个标记，RoPE根据其在序列中的位置对其相应的键向量和查询向量应用旋转。这种旋转是通过将向量与一个旋转矩阵相乘来实现的。然后，旋转后的键向量和查询向量以通常的方式（点积后接softmax）用于计算注意力分数，Transformer中的其余计算照常进行。
让我们看看什么是旋转矩阵，以及它是如何应用到查询向量和键向量上的。
旋转矩阵：二维空间（最简单的情况）中的旋转矩阵如下，其中是任意角度：
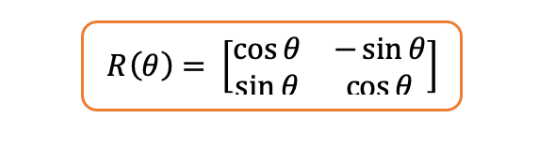
如果你将上述矩阵与二维向量相乘，它只会改变向量的角度，而保持向量的长度不变。你同意吗？
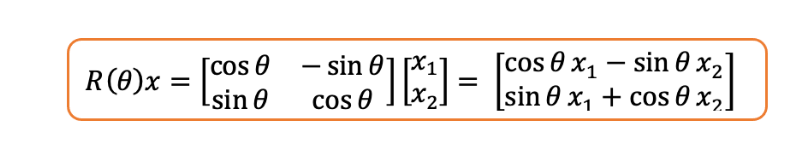
我们可以看到旋转后向量的范数与原始向量相同。让我们来算一下：
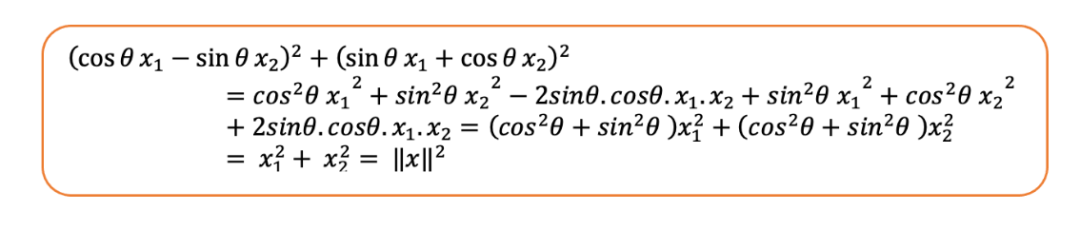
现在，它是如何应用到键向量和查询向量上的呢？
注意，查询向量是查询矩阵和标记嵌入的乘积，即：
现在如果我们对其应用旋转矩阵，我们就是在旋转查询向量。
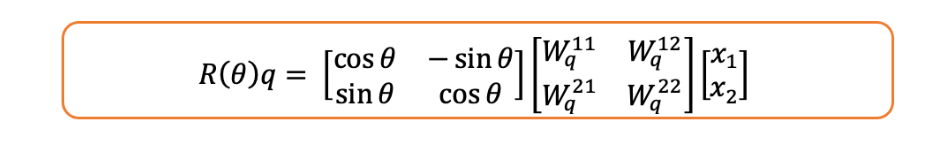
但是，它究竟是如何包含位置信息的呢？
问得好。在上述所有数学运算中，我们假设标记出现在位置1！如果它出现在任意位置，那么旋转矩阵中将包含：
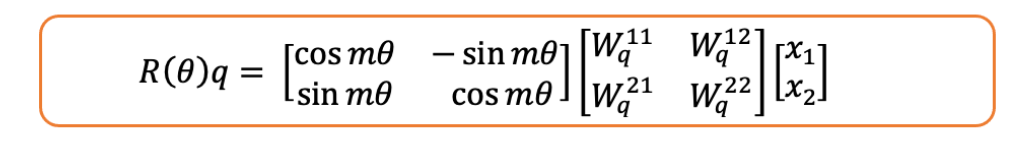
4.3 相对性的数学证明
现在，让我们证明旋转位置嵌入（RoPE）是相对的。为此，我们需要证明两个标记之间的注意力分数仅取决于它们的相对位置，而不是绝对位置。
- 我们将RoPE操作定义如下：
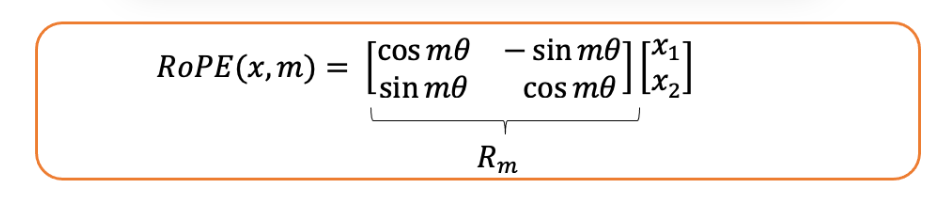
- 考虑两个位于位置和的标记：
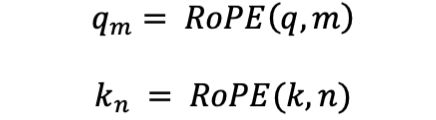
- 我们将注意力分数计算为它们的点积：
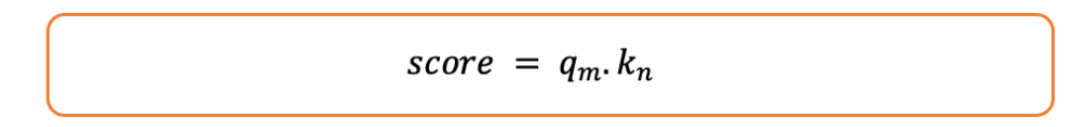
让我们如下展开：
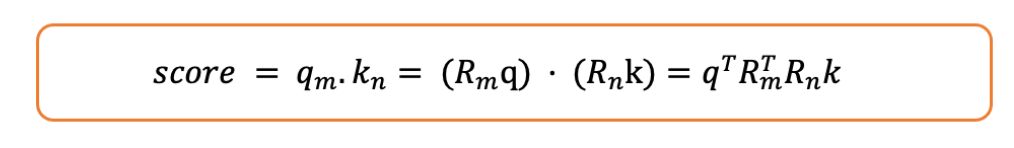
- 旋转矩阵具有这样一个很好的性质：
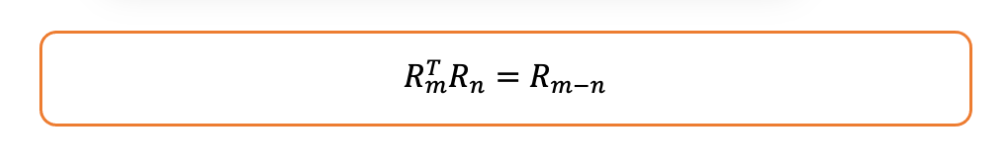
- 因此，注意力分数变为：
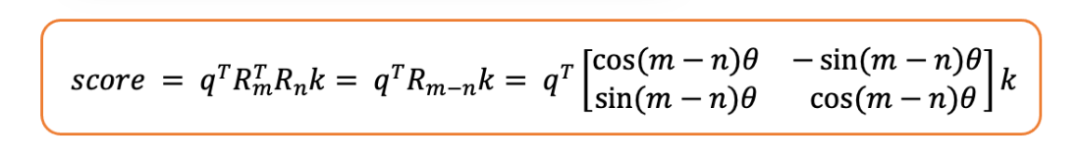
如你所见，分数是相对位置的函数，即和之间位置的差值。
4.4 高维旋转矩阵
通常情况下，模型的嵌入维度不是2，通常比2大得多。那么旋转矩阵会如何变化呢？Roformer论文的作者提出了以下组合方式：
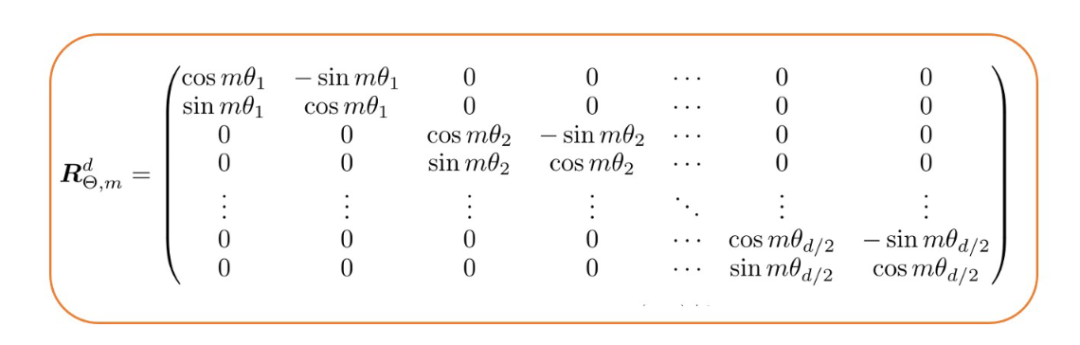
也就是说，对于位置和嵌入维度，旋转矩阵由个2×2的旋转矩阵组成。值得一提的是，由于这种构造是稀疏的，相关研究人员推荐了一种计算效率高的方法来计算它与标记嵌入向量的乘积。
4.5 代码片段：Roformer的实现
旋转位置嵌入（RoPE）的代码实现相当复杂，但本次重点介绍负责计算RoPE的核心功能，它封装在以下方法中：
def apply_rotary_position_embeddings(sinusoidal_pos, query_layer, key_layer, value_layer=None):
# https://kexue.fm/archives/8265
# sin [batch_size, num_heads, sequence_length, embed_size_per_head//2]
# cos [batch_size, num_heads, sequence_length, embed_size_per_head//2]
sin, cos = sinusoidal_pos.chunk(2, dim=-1)
# sin [θ0,θ1,θ2......θd/2-1] -> sin_pos [θ0,θ0,θ1,θ1,θ2,θ2......θd/2-1,θd/2-1]
sin_pos = torch.stack([sin, sin], dim=-1).reshape_as(sinusoidal_pos)
# cos [θ0,θ1,θ2......θd/2-1] -> cos_pos [θ0,θ0,θ1,θ1,θ2,θ2......θd/2-1,θd/2-1]
cos_pos = torch.stack([cos, cos], dim=-1).reshape_as(sinusoidal_pos)
# rotate_half_query_layer [-q1,q0,-q3,q2......,-qd-1,qd-2]
rotate_half_query_layer = torch.stack([-```python
rotate_half_query_layer = torch.stack([-query_layer[..., 1::2], query_layer[..., ::2]], dim=-1).reshape_as(
query_layer
)
query_layer = query_layer * cos_pos + rotate_half_query_layer * sin_pos
# rotate_half_key_layer [-k1,k0,-k3,k2......,-kd-1,kd-2]
rotate_half_key_layer = torch.stack([-key_layer[..., 1::2], key_layer[..., ::2]], dim=-1).reshape_as(key_layer)
key_layer = key_layer * cos_pos + rotate_half_key_layer * sin_pos
if value_layer isnotNone:
# rotate_half_value_layer [-v1,v0,-v3,v2......,-vd-1,vd-2]
rotate_half_value_layer = torch.stack([-value_layer[..., 1::2], value_layer[..., ::2]], dim=-1).reshape_as(
value_layer
)
value_layer = value_layer * cos_pos + rotate_half_value_layer * sin_pos
return query_layer, key_layer, value_layer
return query_layer, key_layer注意，query_layer = query_layer * cos_pos + rotate_half_query_layer * sin_pos这一行代码是根据上一节提到的高效计算方法进行运算的。
结论
在本文中，本文回顾了三种主要的位置嵌入类型：绝对位置嵌入、相对位置嵌入和旋转位置嵌入。绝对位置嵌入提供了一种直接的位置信息编码方式，有学习型和固定型两种方法。相对位置嵌入侧重于标记之间的相对距离，这种方法被应用于像Transformer-XL和DeBERTa等模型中。最后，创新的旋转位置嵌入（RoPE）结合了绝对位置嵌入和相对位置嵌入的优点，为位置信息编码提供了一种更高效、可扩展的解决方案。
本文转载自智驻未来，作者：小智
赞
收藏
回复
相关推荐
