循环变换器中的潜在思维：深度与参数效率的权衡研究

研究背景与创新点

深度学习模型，尤其是大型语言模型（LLMs）在推理任务上的表现令人瞩目。传统观点认为，模型参数量是决定推理能力的主要因素。然而，Google Research团队的这项研究《推理潜在思维：循环变换器的力量》提出了一个更为大胆的观点：许多推理问题主要需要的是足够的深度，而非海量参数。该研究探索了循环变换器（Looped Transformers）在推理任务中的应用潜力，并揭示了模型架构与推理能力之间的深层联系。

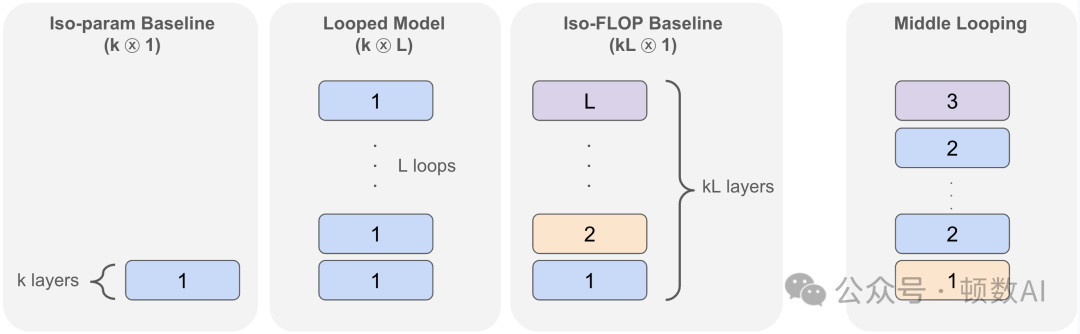
本文的核心创新点在于提出并验证了循环模型在推理任务上的优势。研究表明，一个k层变换器循环L次（表示为(k⊗L)）的性能可以接近甚至超过具有相同计算量但参数量大L倍的非循环kL层模型，同时显著优于参数量相同的k层非循环模型。这一发现不仅适用于合成推理问题，还扩展到了实际语言建模场景，揭示了模型架构设计中的重要权衡。

研究方法与实验设计

研究团队采用了多种方法验证其假设，包括：

1. 合成推理任务实验：研究者设计了三类合成推理任务来测试循环模型的能力：

• n元加法：测试模型对多个三位数进行加法的能力
• p-hop归纳：测试模型在序列中进行多步回溯检索的能力
• i-GSM（合成小学数学问题）：模拟小学数学应用题的计算图问题

2. 语言建模实验：在Pile数据集上预训练1B参数规模的模型，比较不同架构在下游任务上的表现：

• 闭卷问答（测试记忆能力）
• 开卷问答（测试阅读理解能力）
• 数学应用题（测试数学推理能力）
• 推理原语（测试基础推理能力）

3. 理论分析：证明循环模型在特定推理任务上的表达能力，包括：

• 群组合问题的最优深度解
• 循环模型模拟非循环模型的能力
• 循环模型与思维链（Chain-of-Thought）推理的关系

实验设计精巧，通过比较(k⊗L)循环模型与两个基线：参数量相同的(k⊗1)模型和计算量相同的(kL⊗1)模型，全面评估了循环架构的优势与局限。

主要研究发现

1. 循环模型在合成推理任务上的表现

在合成推理任务上，循环模型展现出显著优势。以n元加法为例，即使是循环12次的1层网络，其表现也接近使用12倍参数量的12层基线模型。类似地，在p-hop问题和i-GSM任务上，循环模型也能以少得多的参数达到与非循环模型相当的性能。这表明这些推理任务主要需要的是足够的深度，而非大量参数。

研究者还通过理论分析证明，对于群组合问题，一个1层变换器循环log₂(n)次就能有效解决，这与非循环模型的最佳已知深度上界相匹配。

2. 循环模型在语言建模中的归纳偏置

在语言建模实验中，研究者发现了一个有趣的现象：虽然循环模型的困惑度（perplexity）不如参数量更大的非循环模型，但在需要推理的下游任务上表现出色。具体而言：

• 在记忆型任务（如闭卷问答）上，循环模型的优势有限
• 在推理型任务（如开卷问答、数学应用题）上，循环模型能弥补大部分与参数量更大模型的差距
• 在纯推理原语任务上，循环模型甚至超过了参数量更大的基线模型

这表明循环架构具有促进推理能力的归纳偏置，即使以牺牲一些记忆能力为代价。研究者通过"等困惑度"下游性能比较（isoplots）进一步验证了这一发现。

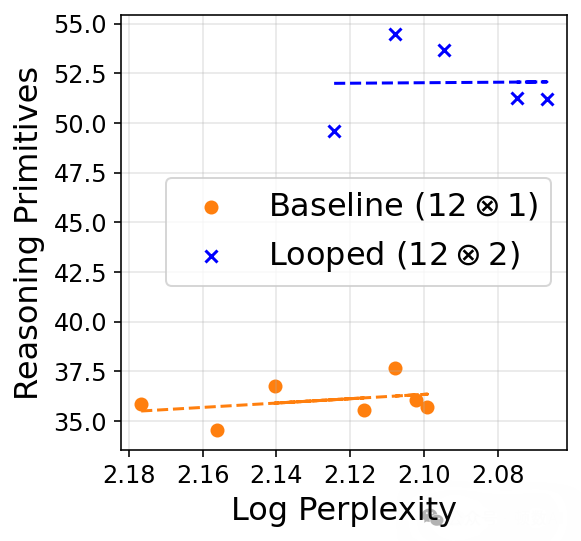
3. 循环深度的缩放行为

研究发现，随着循环次数增加，模型在各类任务上的表现呈现对数缩放规律：

准确率 = α·log(D) + β

其中D为有效深度，α衡量深度对下游性能的影响。不同任务类型的α值不同，推理任务的α值相对更高，表明推理任务从深度增加中获益更多。这种缩放行为类似于思维链（CoT）推理的推理时间缩放。

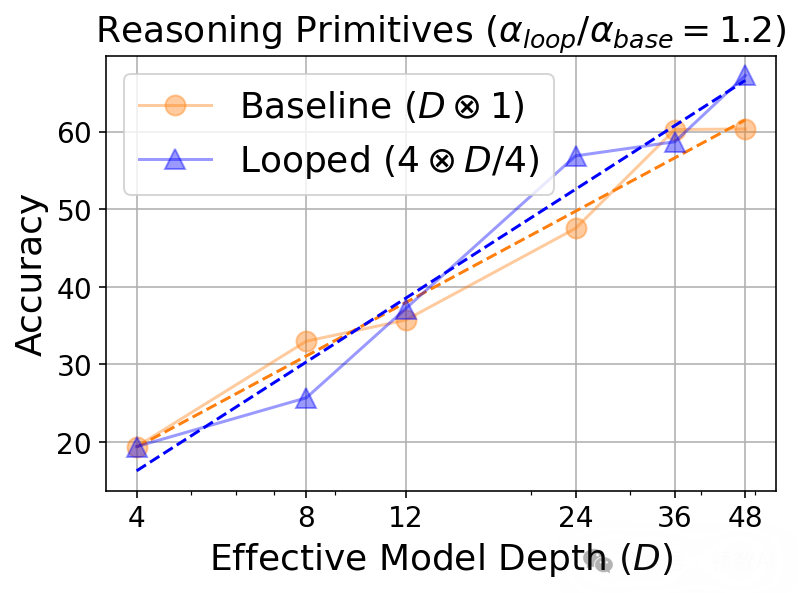
4. 循环模型与思维链推理的联系

研究者提出了循环模型与思维链推理之间的理论联系。思维链推理可以视为一种特殊的循环模型，每次迭代产生一个思维token。而循环模型则更为强大，能在每次迭代中生成多个"潜在思维"。研究者证明了循环变换器能够模拟思维链推理，这解释了为何循环模型在推理任务上表现出色。

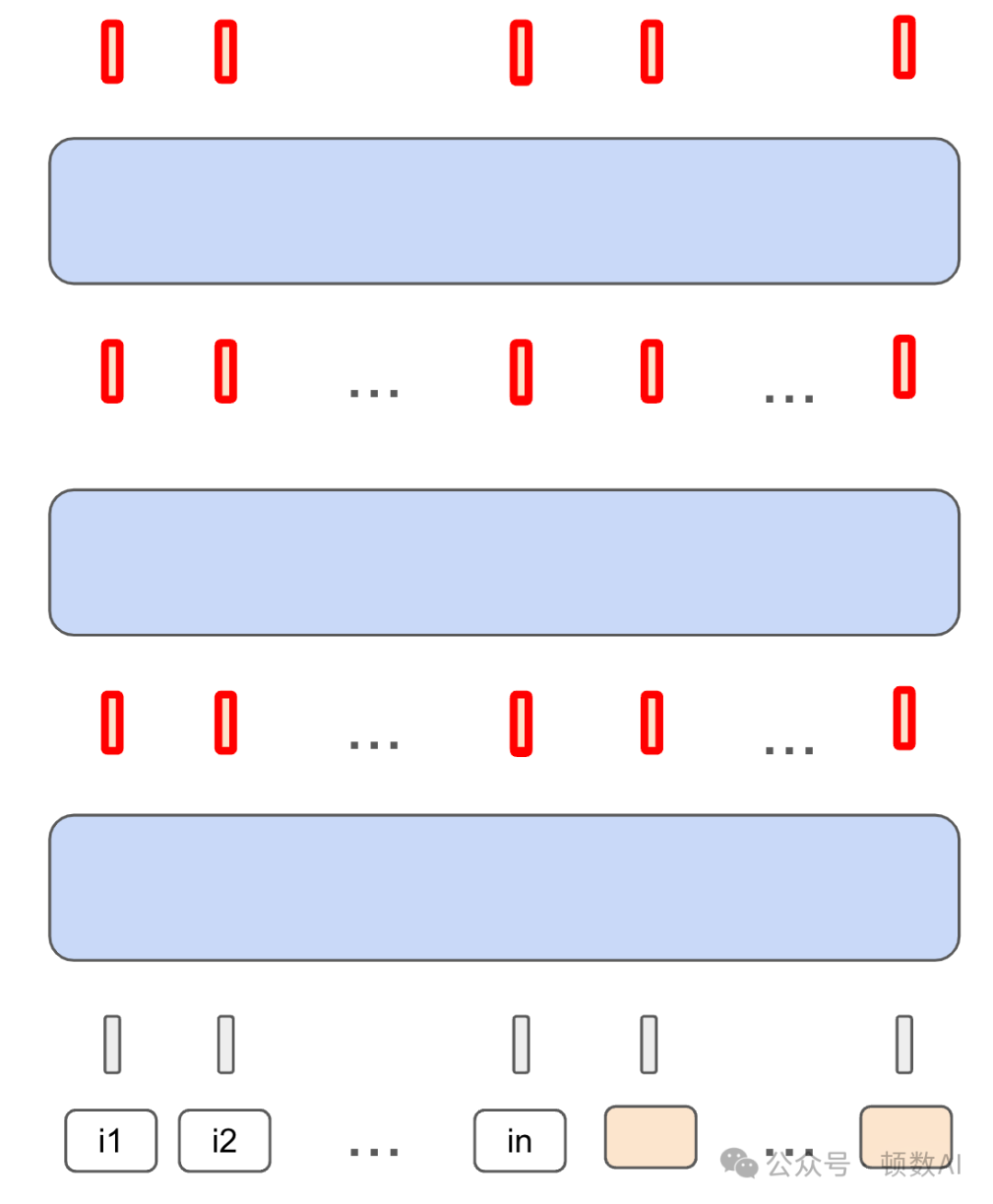
5. 基于循环的正则化方法

基于循环模型对推理的归纳偏置，研究者设计了一种新的正则化方法，通过鼓励模型层之间的相似性来获得循环模型的优势，同时保持非循环模型的灵活性。实验表明，这种正则化方法能在不影响困惑度的情况下提升模型的推理能力。

技术细节分析

循环变换器的数学表示

循环变换器可以形式化表示为重复应用相同的变换器块。给定L层变换器块TB，循环T次的模型可表示为：

p_{θ,T} = OUTPUT ∘ (TB)^T ∘ EMBED

其中OUTPUT是输出层，EMBED是嵌入层，(TB)^T表示变换器块循环应用T次。

理论结果

研究提供了几个重要的理论结果：

1. 群组合定理：对于任何有限群G和n个元素，存在一个1层变换器循环⌈log₂n⌉次就能计算这n个元素的组合，且深度最优。
2. 循环模型模拟定理：具有R个不同层的L层非循环变换器可以被一个循环L次的1层变换器模拟，后者的嵌入维度增加R+2，MLP隐藏维度增加O(L)。
3. CoT模拟定理：任何L层非循环变换器进行m步CoT推理，都可以被一个具有L+O(1)层、循环m次的变换器模拟。

这些理论结果为实验观察提供了坚实的数学基础，证明了循环架构在推理任务上的优势并非偶然。

实现细节

研究中使用的循环变换器实现相对简单，主要是在前向传播中重复应用相同的变换器块。对于(k⊗L)模型，即k层变换器循环L次，总共有k×L层计算，但只有k层的参数。

研究还探索了"中间循环"（Middle Looping）变体，即保留网络开始和结束的独立层，只在中间部分应用循环。这种方法在某些任务上表现更好，表明网络的不同部分可能需要不同程度的参数共享。

研究意义与局限性

研究意义

1. 参数效率提升：研究表明，通过循环架构可以显著减少模型参数量，同时保持甚至提升推理能力，这对于资源受限场景具有重要价值。
2. 推理与记忆的二分法：研究揭示了模型能力中推理与记忆的权衡，为理解大型语言模型的能力提供了新视角。
3. 与思维链的联系：建立了循环架构与思维链推理之间的理论联系，为理解和改进推理机制提供了新思路。
4. 正则化方法：提出的基于循环的正则化方法为提升模型推理能力提供了实用工具。

局限性

1. 推理定义的模糊性：研究中"推理"的定义相对宽泛，不同类型的推理可能需要不同的模型架构。
2. 任务覆盖有限：实验主要集中在特定类型的推理任务，可能不能完全代表所有推理场景。
3. 规模限制：实验主要在1B参数规模进行，更大规模模型的行为可能有所不同。
4. 计算效率权衡：虽然参数量减少，但循环架构在推理时的计算量与非循环模型相同，没有提高推理速度。

未来研究方向

1. 多模态推理：探索循环架构在视觉-语言等多模态推理任务中的应用。
2. 推理形式化：更精确地形式化不同类型的推理问题，理解它们对模型架构的不同需求。
3. 推理时间缩放：进一步探索利用循环模型进行更高效的推理时间缩放，辅助更深层次的推理。
4. 混合架构：结合循环和非循环层的混合架构，平衡推理能力和记忆能力。
5. 更优循环策略：研究不同的循环策略（如选择性循环、动态循环等）对性能的影响。

结论

本研究对循环变换器在推理任务中的应用进行了深入探索，揭示了一个重要发现：许多推理问题主要需要的是计算深度而非大量参数。循环架构通过参数共享实现了深度增加而不增加参数量，在各种推理任务上展现出显著优势。研究还建立了循环模型与思维链推理之间的理论联系，为理解大型语言模型的推理机制提供了新视角。

这些发现不仅有理论意义，还提供了实用价值：通过循环架构或基于循环的正则化，可以构建更参数高效的推理模型。未来研究可进一步探索循环架构在更广泛推理任务中的应用，以及与其他推理增强技术的结合。

总的来说，这项研究为大型语言模型的架构设计提供了新的思路，强调了在追求更强推理能力时，深度与参数量之间的权衡，以及循环架构作为一种有效折中方案的潜力。

论文：https://arxiv.org/abs/2502.17416

本文转载自​​顿数AI​​，作者： 葱葱 ​​​​