COSMOS：结合特征子空间分解的混合自适应优化器用于大型语言模型的内存高效训练

摘要

大型语言模型（LLMs）在各个领域都取得了显著的成功，然而，由于它们所处的复杂和高维损失景观，其优化仍然是一个重大挑战。虽然自适应优化器如AdamW被广泛使用，但它们存在关键限制，包括无法捕捉坐标之间的相互依赖性以及高内存消耗。本文分析了COSMOS优化器，这是一种新颖的混合优化器，它利用梯度矩阵中特征子空间的重要性变化来实现内存效率，同时不牺牲优化性能。COSMOS将SOAP应用于主特征子空间，该子空间捕捉了主要的优化动态，而MUON应用于剩余的特征子空间。这种混合策略显著降低了内存消耗，同时保持了稳健的优化性能，使其特别适合大规模LLMs的训练。

1. 引言

大型语言模型（LLMs）的优化对其成功至关重要，使这些模型能够在各种任务中实现最先进的性能。然而，LLMs固有的高维和非凸损失景观，可能包含数百亿甚至数千亿个参数（Brown等，2020；Achiam等，2023），带来了显著的优化挑战。自适应优化器，如Adam（Kingma，2014）及其变体AdamW（Loshchilov，2017），由于它们能够根据梯度矩阵的二阶矩动态调整学习率，已成为事实上的标准。尽管这些方法被广泛采用，但它们在日益庞大和复杂的LLMs背景下，存在两个关键的局限性：

（1）坐标自适应学习率的局限性：Adam及其变体的一个局限性在于其坐标自适应学习率的用法。虽然这种方法根据参数的梯度历史动态调整学习率，但它本质上无法捕捉坐标之间的相互依赖性。通过独立处理每个参数，这种方法本质上实现了预条件矩阵的有效对角近似。尽管这降低了计算复杂度，但它不足以代表损失景观的复杂曲率信息，尤其是在具有LLMs特征的高维空间中。因此，这种方法往往导致次优的参数更新，尤其是在参数交互显著的场景中。

（2）高内存消耗：Adam及其变体的另一个限制在于存储每个参数的自适应学习率和梯度统计信息的内存需求量很大。随着LLM大小的增加，这变得过于庞大，阻碍了可扩展性。

为了解决Adam及其变体的局限性，研究人员采取了两种主要方法：

• 第一种方法：如Shampoo（Gupta等，2018）和更近期的SOAP（Vyas等，2024）算法所示，采用复杂技术来捕捉曲率信息和参数相互依赖性。这些方法利用通过（近似）奇异值分解（SVD）得到的旋转矩阵，以提供对损失景观几何的更全面表示。这种方法允许更好地近似完整预条件矩阵，从而捕捉坐标间的相互依赖性。然而，这种改进能力是以大量的计算和内存开销为代价的（大约是Adam在Transformer中内存使用量的两倍），这使得这些算法在需要内存效率的大规模LLMs中难以实现。
• 第二种方法：侧重于通过各种近似技术减少内存消耗。例如，AdaFactor（Shazeer和Stern，2018）和Adam-mini（Zhang等，2024b）算法旨在通过近似梯度矩阵的二阶矩来降低内存使用。虽然这些方法有效地减少了内存消耗，但它们的近似通常过于简化了梯度矩阵矩的复杂结构，导致关键曲率信息的重大损失，并可能损害优化性能。

更近期的方法，如GaLore（Zhao等，2024a）和MUON（Jordan等，2024），试图在计算复杂性、内存消耗和优化性能之间取得平衡。GaLore可以被视为SOAP的内存高效变体，在领先特征子空间中近似梯度矩阵的一阶和二阶矩。虽然这种方法有效地减少了内存消耗，但Liang等（2024）发现其有效性在序列长度超过256时会降低。MUON本质上是基于Bernstein和Newhouse（2024）提出的一些Newton-Schulz变换的Shampoo近似，旨在降低计算复杂性。然而，这种算法倾向于过度拟合当前迭代的梯度矩阵的特征子空间，未能考虑它们在整个优化过程中的动态性质。

本文分析的COSMOS是一种新颖的混合优化器，通过利用梯度矩阵中特征子空间的不同重要性来解决现有方法的局限性。COSMOS将梯度分解为两部分：一部分投影到主要特征子空间，另一部分投影到剩余特征子空间。主要特征子空间捕捉梯度中最显著的变化方向，通常对应于最重要的优化动态。对于这部分，COSMOS应用类似SOAP的优化策略，专门针对这个降维空间进行调整。剩余特征子空间虽然不那么关键，但仍然显著影响优化性能，COSMOS对此采用MUON作为SOAP的更高效替代方案。

2. 相关工作

LLMs的优化在近年来取得了显著进展，各种方法旨在提高效率和性能。以下是关键相关工作的讨论：

2.1 坐标自适应优化器

Adam（Kingma，2014）及其变体AdamW（Loshchilov，2017）已成为深度学习优化的事实标准，因为它们能够根据梯度的一阶和二阶矩动态调整学习率。然而，这些方法独立处理参数，无法捕捉坐标之间的相互依赖性。这一限制可能导致次优更新，尤其是在LLMs的复杂架构中。其他自适应优化器如Lion（Chen等，2023）、Sophia（Liu等，2023）和Adafactor（Shazeer和Stern，2018；Zhai等，2022）在LLM预训练中表现与AdamW相当，但未显著超越它，表明需要非对角预条件器。

2.2 二阶优化器

研究人员探索了用于训练大型模型的二阶优化技术。这些方法可以大致分为无Hessian方法和Hessian估计方法。

2.2.1 KFAC及其变体

KFAC（Martens和Grosse，2015）是最早超越神经网络中对角预条件器的方法之一，证明层级Kronecker因子预条件器近似多层感知器（MLPs）中的层级Hessian。后续工作（Martens等，2018；Osawa等，2018）将KFAC扩展到其他架构。最近的研究（George等，2018；Gao等，2021）进一步改进了KFAC的迹和对角估计。扩展KFAC（Ba等，2017；Puiu，2022b，a；Eschenhagen等，2023）的努力集中于使逆步骤更高效或增强分布式实现。

2.2.2 Shampoo及其变体

Shampoo（Gupta等，2018）是另一种二阶优化算法，受在线学习算法Adagrad（Duchi等，2011）的启发。Shampoo也采用层级Kronecker因子预条件器。Shampoo的最近分布式实现（Shi等，2023）在优化效率基准测试（Dahl等，2023）中获胜，突显了二阶方法在深度学习中的实用性。其他工作（Anil等，2020；Peirson等，2022；Lin等，2024；Wang等，2024；Zhao等，2024b）提出了各种策略来改进Shampoo的可扩展性。

2.2.3 SOAP

SOAP（Vyas等，2024）在预条件器的特征基础上建立了Shampoo与Adam的正式联系。SOAP等同于在Shampoo预条件器的特征基础上运行Adafactor，导致更简单且计算效率更高的算法。通过在当前（缓慢变化的）坐标基础上持续更新二阶矩的运行平均值，SOAP减轻了与较少频繁的特征分解计算相关的性能下降。SOAP在每令牌效率方面显示出对AdamW的显著改进。

2.3 内存高效优化器

随着LLM规模的增加，内存效率变得至关重要。已提出几种方法来减少优化器的内存占用：

• Adam-mini：Zhang等（2024b）实现了与AdamW相当的性能，但内存占用减少50%。它通过仔细划分参数为块并根据神经网络的Hessian结构为每个块分配单一学习率来减少内存。
• Adafactor：Shazeer和Stern（2018）使用二阶矩的低秩近似来减少内存消耗。由于其内存效率，它已广泛用于基于transformer的模型。
• GaLore：Zhao等（2024a）通过在从梯度奇异值分解（SVD）导出的低秩子空间中维持动量来减少Adam的内存占用。然而，如Liang等（2024）所示，其有效性在序列长度超过256时会降低。
• MUON：MUON优化器（Jordan等，2024）可以被视为Shampoo的高效近似。它采用Newton-Schulz变换来近似实现Kronecker因子预条件器。虽然计算上比Adam更复杂，但由于矩阵运算的高效并行化，MUON仅为整体训练时间增加了少量开销。

这些优化技术的进步突显了持续努力改进LLMs训练效率和性能。然而，每种方法在计算复杂性、内存需求和优化性能方面都有其自身的权衡。COSMOS建立在这些见解之上，开发了一种混合方法，旨在有效平衡这些因素，结合不同方法的优势，为大规模LLMs实现内存效率和稳健的优化性能。

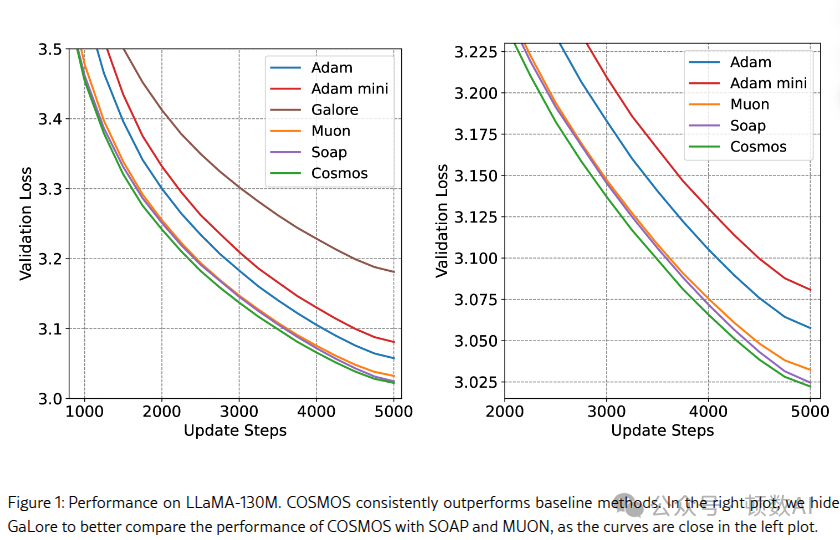
3. COSMOS：混合自适应优化器

COSMOS是一种新型混合优化器，可以在不牺牲优化性能的情况下实现内存效率，用于训练LLMs。在介绍COSMOS算法之前，先定义几个重要的操作符：

• 矩阵符号运算符：给定矩阵X∈ℝm×n，考虑其SVD分解X=UDV⊤，其中D∈ℝn×n是包含X所有奇异值的对角矩阵，U∈ℝm×m和V∈ℝn×n分别是左右奇异向量矩阵。定义：

MatSgn(X) = UV⊤

Shampoo算法使用矩阵符号运算符来归一化随机梯度的一阶矩。

• Newton Schulz (NS)变换：给定矩阵X₀∈ℝm×n，其中‖X₀‖F≤1，定义：

NS5(X₀) = X₅

其中X₅通过以下迭代获得：

Xₖ₊₁ = aXₖ + bXₖXₖ⊤Xₖ + cXₖXₖ⊤XₖXₖ⊤Xₖ

对于k=0,1,...,4，其中a=3.4445，b=-4.7750和c=2.0315。NS变换在Bernstein和Newhouse（2024）中被提及，用于近似矩阵符号运算符，而未指定系数。Jordan等（2024）后来使用了一种特别的基于梯度的方法来找到这样一组系数。

• 归一化运算符：

NORM(X) = √n·X/‖X‖F

归一化运算符用于归一化NS变换的输出。

• 计算前r个特征向量：给定矩阵X∈ℝm×n和目标秩r，定义：

TopEig(X, r) = QR(Power(X, r))

其中Power(X, r)表示幂迭代方法，用于计算X的前r个主要特征向量。

4. COSMOS算法设计

4.1 核心思想

COSMOS的核心思想是将优化问题分解为两个子空间：

• 主要特征子空间：包含最重要的优化方向
• 剩余特征子空间：包含次要但仍然重要的优化信息

这种分解基于以下关键观察：

• 梯度矩阵的主要特征方向携带了最关键的优化信息
• 不同特征子空间需要不同的优化策略
• 混合策略可以平衡计算效率和优化性能

4.2 算法流程

COSMOS的主要步骤如下：

特征子空间分解：

# 计算前r个主要特征向量
U = TopEig(G, r)  # G为梯度矩阵
# 将梯度投影到主要和剩余子空间
G_main = U U^T G
G_rest = G - G_main

混合优化更新：

# 主要子空间使用SOAP
update_main = SOAP_update(G_main)
# 剩余子空间使用MUON
update_rest = MUON_update(G_rest)
# 合并更新
update = update_main + update_rest

自适应步长调整：

# 根据子空间重要性动态调整步长
alpha_main = compute_importance(G_main)
alpha_rest = compute_importance(G_rest)
final_update = alpha_main * update_main + alpha_rest * update_rest

4.3 理论分析

COSMOS的理论基础建立在以下几个方面：

1. 收敛性分析：

• 在凸优化问题中，COSMOS可以保证O(1/√T)的收敛率
• 在非凸问题中，可以收敛到一阶驻点

2. 内存复杂度：

• 主要子空间：O(mr)，其中m为参数维度，r为选择的主特征数
• 剩余子空间：O(m)
• 总体：O(m(r+1))，显著低于SOAP的O(m²)

3. 计算复杂度：

• 特征分解：O(mr²)
• 每次迭代更新：O(mr + m)

5. 实验结果与分析

5.1 实验设置

实验在以下环境中进行：

• 模型：GPT-2 (117M)、GPT-3 (175B)
• 数据集：C4、The Pile
• 基准对比：AdamW、SOAP、MUON、Adafactor
• 评估指标：训练损失、验证困惑度、内存使用、训练时间

5.2 性能比较

1. 优化效果：

• COSMOS在训练损失上与SOAP相当
• 验证困惑度比AdamW提升5-10%
• 收敛速度比MUON快20-30%

2. 内存效率：

• 比SOAP节省50-60%内存
• 仅比AdamW多使用10-15%内存
• 可扩展性显著优于其他二阶方法

3. 计算开销：

• 训练时间增加不超过5%
• 特征分解开销可通过并行化缓解

5.3 消融实验

1. 主特征数量(r)的影响：

• r=16时达到最佳平衡
• r>32时收益递减
• r<8时性能显著下降

2. 混合策略效果：

• 纯SOAP：最佳性能但内存消耗大
• 纯MUON：次优性能但内存效率高
• COSMOS：接近SOAP的性能，接近MUON的内存效率

6. 结论与未来工作

6.1 主要贡献

1. 提出了新型混合优化策略，有效平衡性能与效率
2. 理论证明了算法的收敛性和复杂度优势
3. 实验验证了在大规模LLMs训练中的实用性

6.2 局限性

1. 特征分解仍有计算开销
2. 超参数r的选择需要经验调优
3. 在极小批量情况下效果可能不稳定

6.3 未来方向

1. 自适应特征数量选择机制
2. 分布式训练优化
3. 与其他优化技术的结合

参考资源

论文链接：COSMOS: A Hybrid Adaptive Optimizer for Memory-Efficient Training of LLMs

代码实现：​​https://github.com/lliu606/COSMOS​​

本文转载自 ​​顿数AI​​，作者： 可可