小而美！1B模型如何通过测试时优化逆袭405B LLM？

今天分享一篇来自上海人工智能实验室、清华大学、哈尔滨工业大学和北京邮电大学联合的一篇文章，标题是：Can 1B LLM Surpass 405B LLM? Rethinking Compute-Optimal Test-Time Scaling（1B 的 LLM 能否超越 405B 的 LLM？重新思考计算最优的测试时缩放）。

这篇文章研究了大型语言模型（LLMs）在「推理阶段通过增加计算量来提高性能的测试时缩放」（Test-Time Scaling, TTS）方法。作者们「系统地分析了策略模型、过程奖励模型（PRMs）和问题难度如何影响 TTS」，并提出了两个核心问题：「(1) 在不同的策略模型、PRMs 和问题难度水平下，扩展测试时计算的最佳方法是什么？(2) 扩展计算能在多大程度上提高 LLMs 在复杂任务上的性能，以及较小的语言模型是否能通过这种方法超越较大的模型？」

该方法的主要特点包括：

1. 「全面评估」：对不同的 TTS 方法进行了全面的评估，使用了各种最新的策略模型、多个 PRMs、不同的缩放方法和更具挑战性的任务。
2. 「奖励感知」：强调了在 TTS 过程中考虑奖励的必要性，并引入了奖励感知的计算最优 TTS。
3. 「小模型潜力」：实证结果表明，较小的语言模型通过 TTS 有可能超越较大的模型。

一、概述

• 「Title:」Can 1B LLM Surpass 405B LLM? Rethinking Compute-Optimal Test-Time Scaling
• 「URL:」​​https://arxiv.org/abs/2502.06703v1​​
• 「Authors:」Runze Liu, Junqi Gao, Jian Zhao, Kaiyan Zhang, Xiu Li, Biqing Qi, Wanli Ouyang, Bowen Zhou
• 「Code:」​​https://ryanliu112.github.io/compute-optimal-tts​​

1 Motivation

• 当前测试时间缩放（TTS）的研究缺乏对策略模型、过程奖励模型（PRM）和问题难度如何影响TTS的系统分析，限制了对TTS方法理解和实际应用。
• 如何在不同的策略模型、PRM和问题难度级别上优化测试时间计算的缩放方法？
• 扩展计算能在多大程度上提高LLM在复杂任务上的性能，以及小模型是否可以通过这种方法超越大模型？

2 Methods

「省流版总结:」

本文提出了一种计算最佳的TTS策略，通过综合实验分析了策略模型、PRM和问题难度对TTS的影响。实验使用了MATH-500和AIME24数据集，以及不同大小的Llama 3和Qwen2.5模型。研究发现，计算最佳的TTS策略高度依赖于策略模型、PRM和问题难度的选择。

• 「问题建模」: 将推理问题建模为马尔可夫决策过程 (MDP)。
• 「测试时缩放方法」: 考虑了三种 TTS 方法：Best-of-N (BoN), Beam Search, 和 Diverse Verifier Tree Search (DVTS) 。
• 「计算最优的测试时缩放」: 选择超参数以最大化给定测试时策略的性能。
• 「Reward-Aware Compute-Optimal TTS:」将奖励集成到计算最优的 TTS 策略中，形成更通用的框架。

「详细方法和步骤:」

论文通过以下步骤详细阐述了其方法：

• 「问题形式化」：

将推理问题定义为马尔可夫决策过程（MDP），包括状态空间、动作空间、转移函数、奖励函数和折扣因子。

策略根据当前状态生成动作，状态根据动作进行转移，并获得奖励。

目标是找到最优策略，最大化累积奖励。

• 「测试时缩放方法」：

• 「Best-of-N (BoN)」：策略模型生成 N 个响应，然后应用评分和投票方法选择最终答案。
• 「Beam Search」：给定束宽 N 和束大小 M，策略模型首先生成 N 个步骤。验证器选择最佳的 N/M 个步骤进行后续搜索。下一步，策略模型对每个选定的先前步骤采样 M 个步骤。此过程重复，直到达到最大深度或生成标记。
• 「Diverse Verifier Tree Search (DVTS)」：通过将搜索过程划分为 N 个子树来扩展 Beam Search，每个子树使用 Beam Search 独立探索。

「目标:」  这个公式旨在找到一个最优的测试时计算缩放策略（compute-optimal test-time scaling strategy），简单来说就是「怎么用最合理的计算资源，让模型在推理的时候表现最好」。

「符号说明:」

「公式含义:」

提出了一个测试时计算最优缩放策略，该策略选择超参数以最大化给定测试时策略在特定提示上的性能收益。

「符号说明 (与公式2对比):」

「公式含义:」

「公式3与公式2的区别:」

• 提出应将奖励整合到计算最优 TTS 策略中。

1. 「绝对问题难度标准」：

• 使用绝对阈值而不是分位数来衡量问题难度。
• 基于 Pass@1 准确率定义了三个难度级别：easy (50% ~ 100%)、medium (10% ~ 50%) 和 hard (0% ~ 10%)。

3 Conclusion

• 计算最佳的「TTS策略高度依赖于策略模型、PRM和问题难度的选择。」
• 通过「计算最佳的TTS策略，极小的策略模型可以胜过更大的模型。例如，一个1B的LLM可以在MATH-500上超过一个405B的LLM。」
• 实验结果表明，「与CoT和多数投票相比，计算最佳的TTS可以提高LLM的推理性能。」

4 Limitation

1. 将TTS扩展到更多任务，如编码和化学任务。
2. 探索更有效的计算最佳TTS方法。

二、详细内容

1 奖励会显著影响生成的过程和结果

image-20250216224908584

说明：

1. RLHFlow-PRM-Mistral-8B对短响应给予高奖励，却产生了错误的答案；
2. 使用RLHFlow-Deepseek-PRM-8B进行搜索虽然产生正确答案，但使用了更多token。

结论：奖励应该被整合到计算最优的TTS策略中。

2 PRM的过程监督能力是决定其在TTS中性能的关键因素

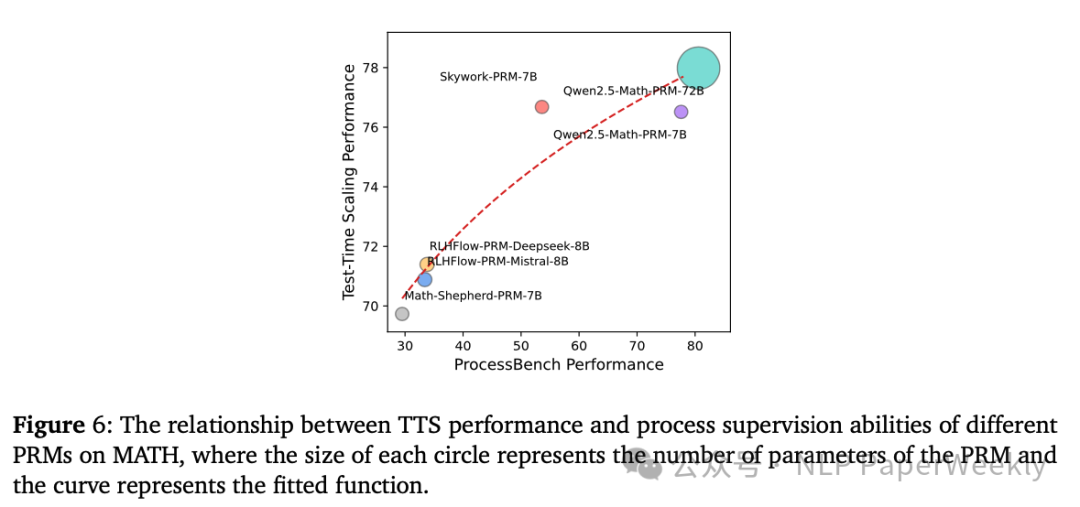
image-20250216225517615

说明：PRM的过程监督能力越强，其在TTS中通常能带来更好的性能。

结论：应该注重提高PRM的过程监督能力，而不仅仅是增加参数量。

3  策略模型大小对TTS参数的影响

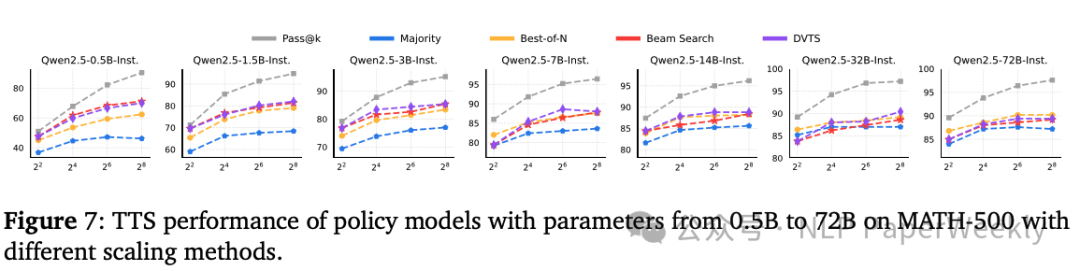
image-20250216225948348

说明：使用了Qwen2.5系列的不同大小LLM（从0.5B到72B）进行实验，分析最优TTS参数。

结论：

• 小型策略模型：基于搜索的方法优于BoN3。对于大型策略模型，BoN比基于搜索的方法更有效。
• 最优的TTS方法依赖于策略模型的大小，在选择TTS方法时需要考虑模型的推理能力。

4 题目难度对TTS参数的影响

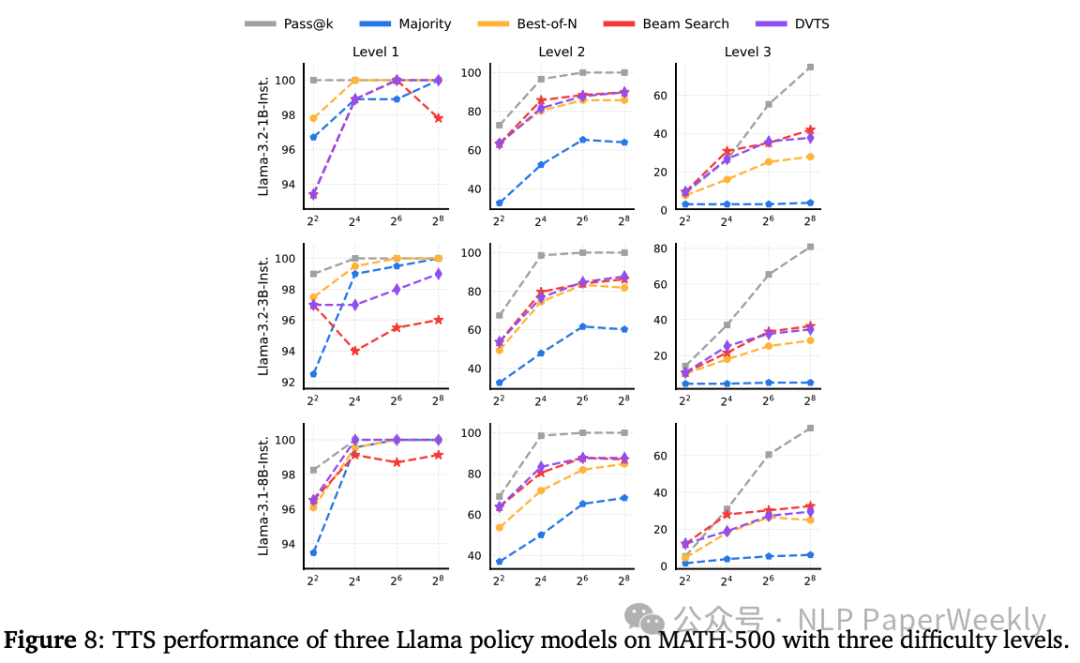
image-20250216230308416

结论：

• 「小规模策略模型（参数少于7B）」：BoN在简单问题上表现更好，而束搜索更适合解决较难问题。
• 「中等规模策略模型（参数7B至32B）」：DVTS在简单和中等问题上表现优异，束搜索则在困难问题上更具优势。
• 「大规模策略模型（参数72B）」：BoN在所有难度级别上均为最佳选择。

5 小模型在TTS加持下可以击败例如DeepSeek-R1, O1, GPT-4o等模型

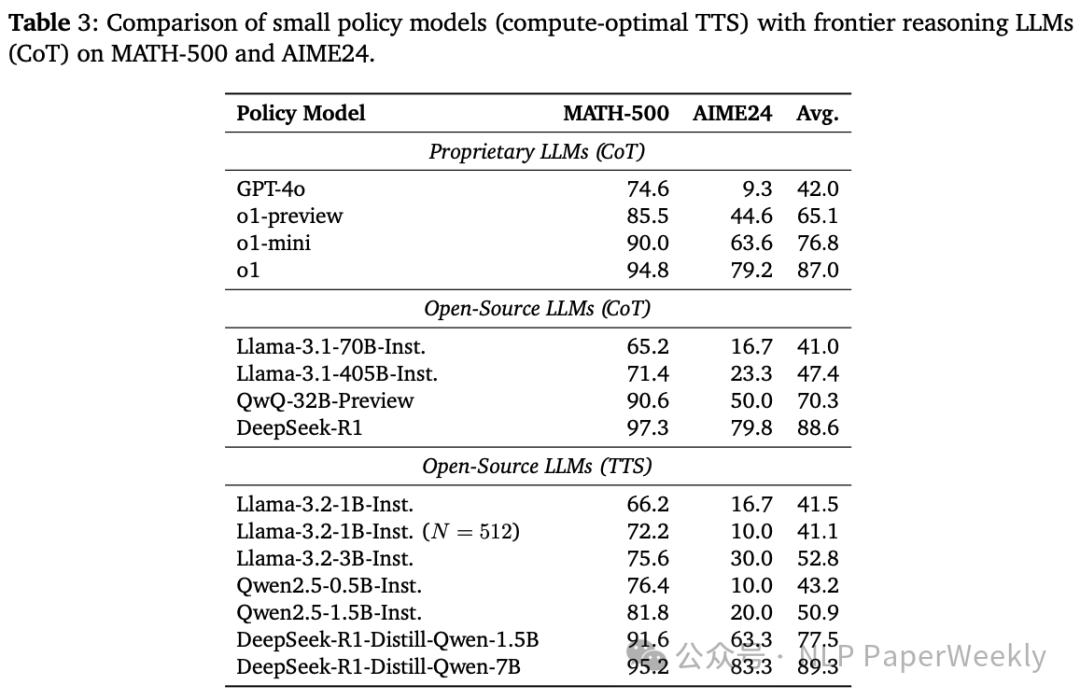
结论：

• 1B模型在TTS加持下能超过405B的模型。
• TTS加持下，DeepSeek-R1蒸馏系列的模型(1.5B和7B模型)能超过DeepSeek-R1。

6 TTS最优相对COT能显著提升推理能力同时提高效率

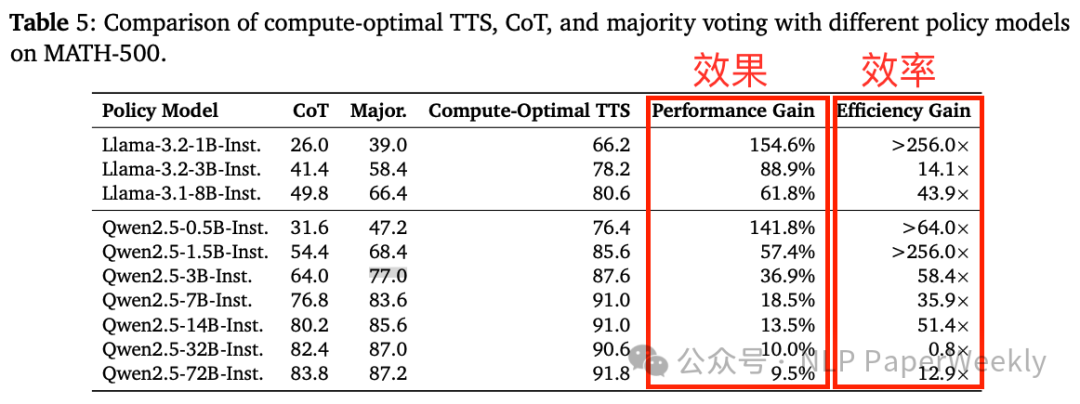
结论：

• 对于推理能力较弱的模型，Scaling测试时计算会带来显著改进；
• 而对于推理能力较强的模型，提升效果则较为有限。

7 TTS比RL或者SFT加持更有效但是比不过R1蒸馏的模型

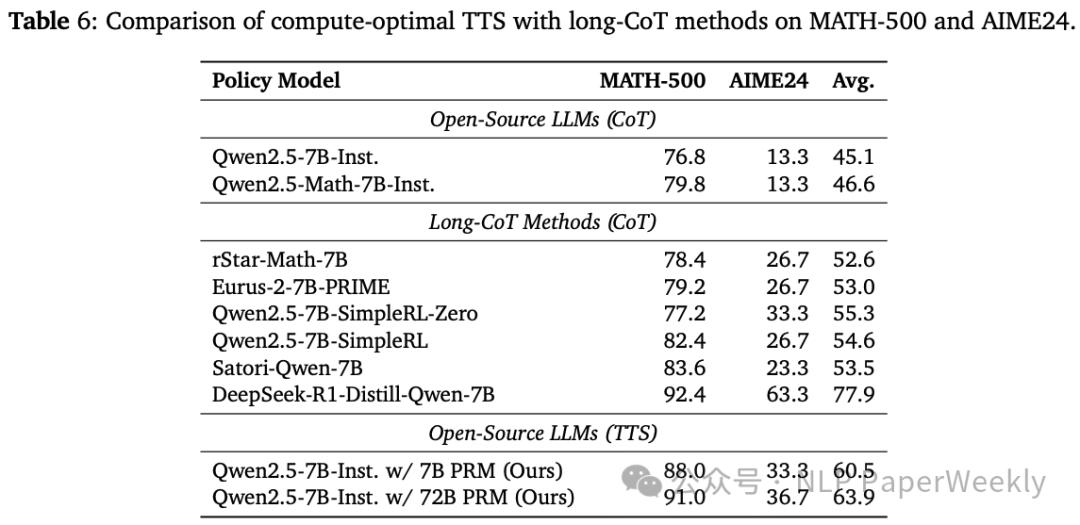
三、总结

本文对计算最优的测试时缩放进行了深入的实证分析，从不同的策略模型、PRMs 和更具挑战性的评估任务的角度出发。研究结果「验证了较小的语言模型在应用计算最优 TTS 时可以表现得比更大的模型更好。」 结果表明，一个 1B 模型可以通过 TTS 实现比 405B 模型更好的性能。此外，还证明了一个 7B PRM 可以通过监督一个更有能力的 72B 策略模型来实现强大的 TTS 结果，这表明了研究真正的“弱到强”方法的重要性，而不是目前用于策略优化的“强到弱”监督。为了实现这一目标，需要开发更有效的监督方法，因为基于 PRM 和基于 RL 的方法由于依赖于高质量的监督而存在局限性。未来的工作应侧重于开发更具适应性和通用性的监督机制，以提高小型语言模型在复杂任务上的性能，并提供开发高效推理策略的新方法。

「结论1:」 通过自适应地调整测试时计算量，「小规模语言模型在特定任务上可以达到甚至超过大规模模型的性能，实现了更高的效率。」

「结论2:」  最佳的「测试时计算缩放策略高度依赖于所使用的策略模型、过程奖励模型（PRM）以及问题的难度。」 这意味着没有一种通用的TTS策略适用于所有情况，需要根据具体任务和模型进行调整。

「结论3:」 本文通过实证分析揭示了「计算最佳TTS策略的依赖性，强调了在实际应用中考虑奖励信息的重要性」，并为未来的研究方向提供了指导。

本文转载自 ​​NLP PaperWeekly​​，作者： NLP PaperWeekly