基于文本的可解释AI局部代理模型稳定性估计分析
论文概述
本文针对可解释人工智能(XAI)中的一个关键问题展开研究 - 局部代理模型在文本领域中的稳定性估计。研究重点关注了相似度度量方法对XAI稳定性评估的影响,并提出了一种基于同义词权重的新型评估框架。
研究背景
可解释AI的重要性
随着AI/ML技术的快速发展,模型的复杂度不断提高,其内部工作机制越来越难以理解。这种"黑盒"特性在医疗、金融等高风险领域尤其令人担忧。例如:
- 医疗诊断系统的错误判断可能导致严重后果
- 金融模型的决策失误可能造成重大损失
- 自动驾驶系统的识别错误可能威胁生命安全
为解决这一问题,可解释AI(XAI)技术应运而生,旨在帮助开发者和用户理解模型的决策依据。
局部代理模型
在XAI方法中,一种常用的技术是构建局部代理模型(Local Surrogate Models)。这种方法通过生成一个简化的、可解释的模型(如决策树或线性回归)来近似复杂模型的局部行为。其中最具代表性的是LIME(Local Interpretable Model-agnostic Explanations)方法。
然而,这些代理模型本身也面临着稳定性问题 - 输入的微小变化可能导致解释结果发生显著变化。这种不稳定性严重影响了XAI方法的可信度。
研究方法
相似度度量方法分析
本文系统研究了四种主要的相似度度量方法:
1.Jaccard指数
- 基于集合交并比计算相似度
- 计算公式:
2.Kendall's Tau距离
- 计算排序列表中的对偶逆序数
- 适用于不等长列表比较
3.Spearman's Footrule
- 计算特征位置差异的L1距离
- 设置了合理的缺失元素惩罚机制
4.基于排序的重叠度量(RBO)
- 通过收敛级数加权计算交集
- 可调节参数p控制top-k特征的权重
同义词权重方案
本文创新性地提出了一种基于同义词的权重计算方案:
- 映射机制
- 建立原始解释与扰动解释之间的特征映射
- 处理不同长度列表的对应关系
- 相似度函数
- 定义Syn(a,b)函数计算特征间的同义程度
- 取值范围[0,1],1表示完全相同,0表示完全无关
- 权重整合
- 将同义词权重整合到现有相似度度量中
- 设计了合理的惩罚机制处理未匹配特征
实验评估
实验设置
实验使用了两个数据集:
- Twitter性别偏见数据集(平均11词/文档)
- 症状诊断数据集(平均29词/文档)
使用DistilBERT作为基础模型,通过LIME生成解释。对每个相似度度量方法,在不同阈值(30%, 40%, 50%, 60%)下测试攻击成功率。
实验结果
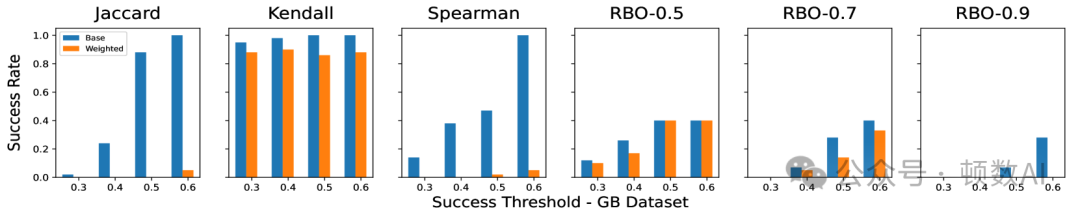
主要发现:
- 标准度量方法的局限性
- Kendall's Tau过于敏感,几乎100%攻击成功率
- Jaccard和Spearman在高阈值下表现不稳定
- 同义词权重的改进效果
- 显著降低了Jaccard和Spearman的敏感度
- RBO方法受益相对较小,可能由于其固有的权重机制
- 数据集影响
- 两个数据集上的结果基本一致
- 文档长度对稳定性评估影响有限
研究贡献
- 理论贡献
- 首次系统分析了相似度度量对XAI稳定性评估的影响
- 提出了创新的同义词权重框架
- 实践意义
- 为XAI方法的稳定性评估提供了更准确的工具
- 帮助识别和改进现有评估方法的局限性
- 应用价值
- 提高了XAI系统在实际应用中的可靠性
- 为后续研究提供了重要的方法论参考
局限性与展望
研究局限
- 方法局限性
- 仅针对LIME进行了详细验证
- 同义词权重方案可能需要进一步优化
- 实验局限性
- 未能包含更多类型的数据集
- 计算开销限制了大规模验证
未来展望
- 方法扩展
- 探索更多相似度度量方法
- 优化同义词权重的计算方案
- 应用拓展
- 验证在其他XAI方法上的效果
- 研究在不同领域的适用性
结论
本研究深入分析了相似度度量方法在评估XAI稳定性中的作用,提出了基于同义词权重的改进方案。研究结果表明:
- 相似度度量的选择对XAI稳定性评估有重要影响
- 传统度量方法存在明显的局限性
- 同义词权重能有效改善评估准确性
这些发现为提高XAI系统的可靠性提供了重要的理论和实践指导。
论文链接: https://arxiv.org/abs/2501.02042

















