深度学习的‘黄金法则’：为什么选择ReLU？

ReLU（Rectified Linear Unit）函数详细讲解

ReLU（修正线性单元）是一种在深度学习中非常流行的激活函数，它主要用于神经网络中的隐藏层。ReLU的设计简单而高效，能够有效地处理梯度消失问题，使深度神经网络得以训练。

1. ReLU函数的定义

ReLU的数学表达式非常简洁：

f(x)=max⁡(0,x)

意思是：

• 当输入值x大于0时，输出值就是输入值x。
• 当输入值x小于或等于0时，输出值是0。

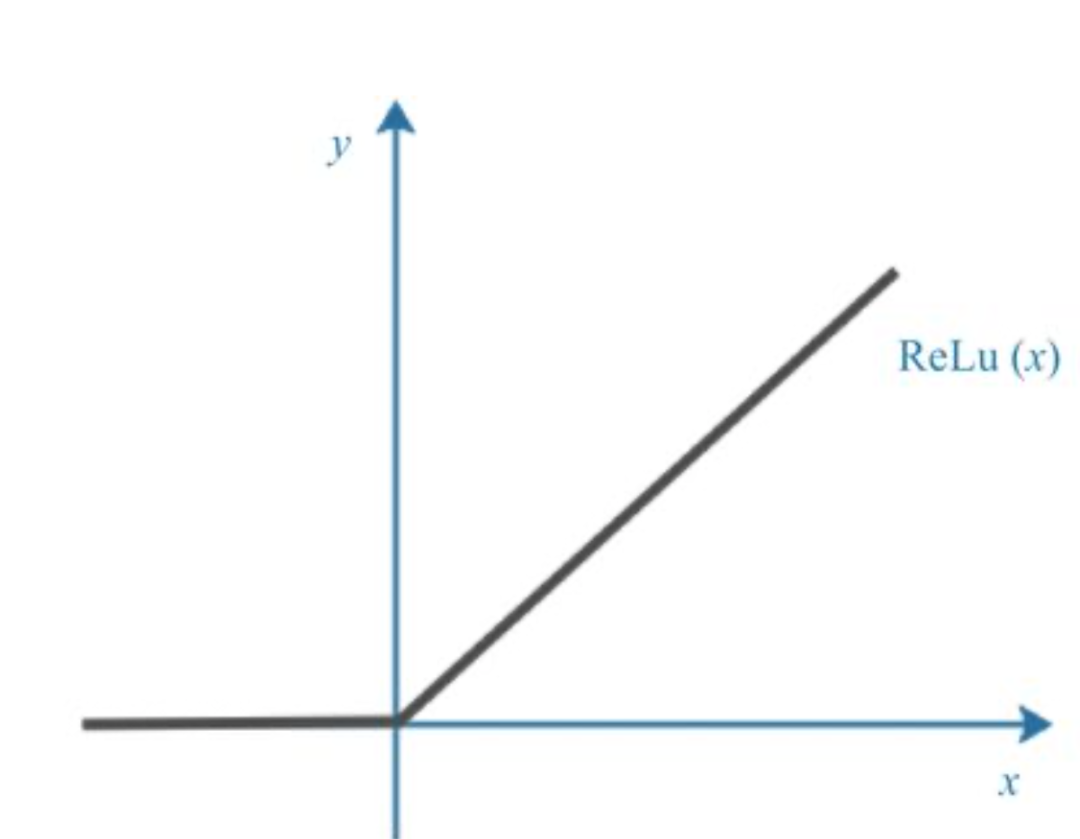
2. ReLU函数的图形

ReLU函数的图形形状呈现为分段线性函数，在输入为负数时输出为0，输入为正数时输出与输入成正比（即y=x）。

​​
​​

3. ReLU的优点

ReLU的优势主要体现在以下几个方面：

• 简洁且高效的计算

    ReLU函数的定义非常简单：f(x)=max⁡(0,x)

这意味着：

如果输入值x大于0，则输出为x；

如果输入值x小于或等于0，则输出为0。

由于ReLU的计算方式非常直接，它无需复杂的指数运算，相比于Sigmoid或Tanh等激活函数，ReLU的计算速度更快。因此，ReLU在大型神经网络中的应用可以大大加快训练速度。

• 解决梯度消失问题

    在传统的Sigmoid或Tanh激活函数中，当输入值非常大或非常小时，导数（梯度）变得非常小。这种现象称为梯度消失，它会使得反向传播时的梯度在传递过程中逐层衰减，导致网络训练困难，甚至无法更新参数。而ReLU的导数在正区间为常数1，负区间为0，几乎不受到输入值大小的限制。这样，ReLU能够有效避免梯度消失的问题，尤其在深度网络中表现得尤为突出。

• 非线性特性

    尽管ReLU函数看起来是一个线性函数，但它通过“截断”负值区域（使其为0）引入了非线性特性。这是因为神经网络需要非线性激活函数来拟合复杂的数据分布和关系。如果没有非线性激活函数，整个网络将变成一个线性模型，无法学习到复杂的特征。因此，ReLU提供了所需的非线性特性，同时保持了计算的高效性。    

• 避免饱和问题

    Sigmoid和Tanh等激活函数容易出现饱和现象，尤其是在输入值很大或很小时，函数的导数会趋近于0，从而导致梯度消失。而ReLU在正区间内没有饱和问题，输出随输入增大而线性增加。这使得ReLU能够更有效地进行权重更新，提高网络的训练效率。

• 稀疏激活（Sparsity）

    ReLU函数的一个特点是，当输入小于0时，输出为0，这意味着神经网络中一部分神经元的输出会是零。通过这种机制，ReLU激活函数可以产生稀疏激活，即在每次前向传播时，大多数神经元的输出为零。这种稀疏性类似于生物神经元的活动模式，有助于提高网络的表示能力，同时也减小了计算量。

• 计算稳定性

由于ReLU不涉及复杂的指数运算（如Sigmoid或Tanh），它能够保持计算的稳定性。在长时间的训练过程中，ReLU也能有效避免由于数值过大或过小而导致的溢出或下溢问题。这使得ReLU在大规模深度神经网络训练中，表现出良好的数值稳定性。

4. ReLU的缺点

尽管ReLU具有很多优点，但它也有一些潜在的缺点：

• 死神经元问题（Dying ReLU Problem）：当ReLU函数的输入值为负时，它的输出始终为0，这意味着神经元在某些情况下可能永远不会激活（即其输出为0）。这种情况会导致部分神经元在训练过程中“死亡”，无法参与到后续的学习。特别是在初始化时，如果某些神经元的权重偏移值过大或过小，可能导致它们在训练过程中始终无法激活。

5. ReLU的变种

为了解决ReLU的一些问题（如死神经元问题），研究者提出了ReLU的几个变种，常见的包括：

1.Leaky ReLU

Leaky ReLU在ReLU的基础上进行改进。它允许负输入时有一个非常小的斜率（通常是0.01），从而避免了“死神经元”问题。其数学表达式为：

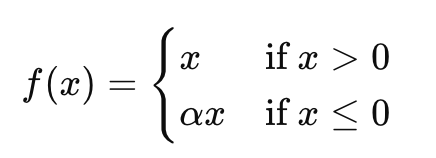
其中，α是一个小常数，通常为0.01。Leaky ReLU确保了即使在负值区域，神经元也会有一个小的梯度，从而避免神经元“死亡”。

2.Parametric ReLU（PReLU）

PReLU是Leaky ReLU的扩展，α（负区域的斜率）不再是固定值，而是可学习的参数，这样网络能够根据训练数据调整每个神经元的行为。

3.Exponential Linear Unit（ELU）

ELU通过在负区域使用指数函数来生成负值输出，从而使得激活函数在负区域也能有非零梯度。ELU通常可以加速训练并提高模型性能。

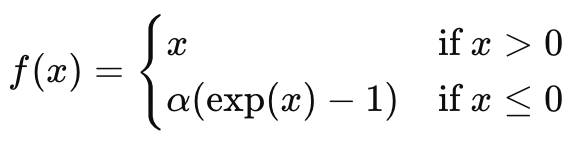
其中，α是一个常数，通常为1。

6. 举例说明

假设我们有一个包含3个神经元的简单神经网络，每个神经元的输入值分别为：x1=3,x2=−1,x3=5，我们将使用ReLU激活函数来计算这些神经元的输出。

输入值：

• x1=3
• x2=−1
• x3=5

应用ReLU函数：

1. 对于x1=3，因为3 > 0，所以输出f(x1)=3
2. 对于x2=−1，因为-1 < 0，所以输出f(x2)=0
3. 对于x3=5，因为5 > 0，所以输出f(x3)=5

总结：

• 输入[3,−1,5]
• 经过ReLU激活函数后，输出变为[3,0,5]

这个简单例子展示了ReLU如何将负值转换为0，而正值保持不变。

7. 总结

ReLU函数在现代深度学习模型中得到了广泛的应用，特别是在卷积神经网络（CNN）和深度神经网络（DNN）中。它不仅具有简单、高效、非线性的特点，而且能够缓解梯度消失问题。不过，它的死神经元问题也促使人们开发了Leaky ReLU、PReLU等变种。总体来说，ReLU是深度学习中非常重要的激活函数，尤其在深层网络的训练中，ReLU可以显著提高网络的训练效率和性能。

本文转载自 人工智能训练营，作者： 小A学习