从“Nature局部核重整化学习机制”说开去

局部核重整化学习机制

自然通讯2025年1月10日刊发一篇题为“局部核重整化作为超参数化卷积神经网络中特征学习的机制” 的文章【文献1】，学者们称“确定了一种完全不同的内核重整化形式：全连接架构的内核只是由单个标量参数全局重整化，而卷积核则经历局部重整化，这意味着网络可以选择局部分量，这些分量将以数据依赖的方式为最终预测做出贡献”。

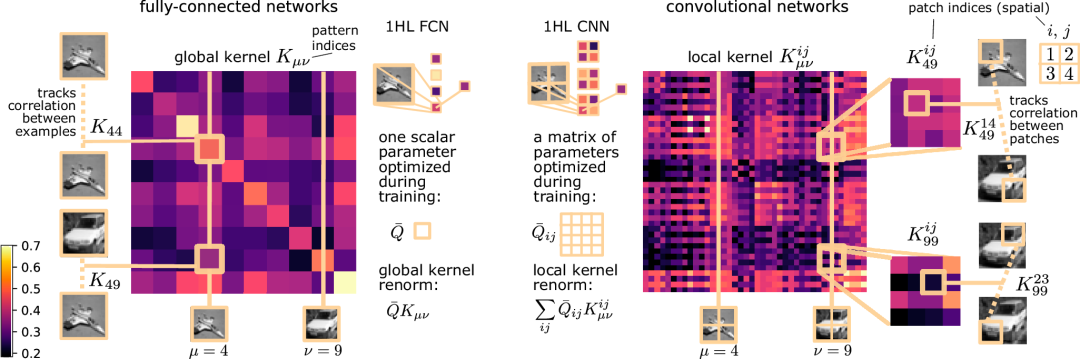
这一发现强调了一种简单的特征学习机制，CNN的重整化内核表达式中展示的核重整化的精确形式就是学者们定义的局部核重整化。该矩阵𝑄¯为所考虑的卷积神经网络（CNN）模型中的特征学习提供了一个紧凑的描述：

在训练过程中优化的特征矩阵元素𝑄¯ij实际上与局部协方差矩阵的 ⌊N0/S⌋ 个补丁对的组合一一对应，而这些补丁又是由训练集元素 xμ 的补丁定义的。可以将矩阵𝑄¯解释为一个特征、数据相关的矩阵，表示局部核的给定分量对重整化核的贡献程度。

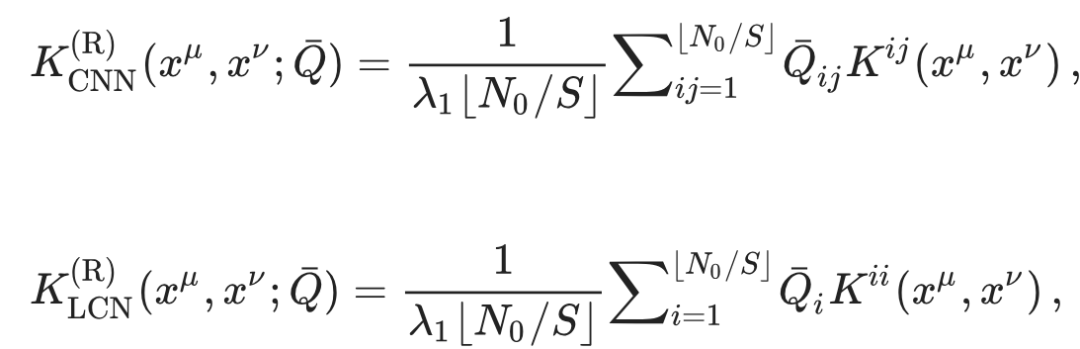
特征矩阵元素 𝑄ij也具有自然的物理解释，作为对应于补丁(i,j)的读出向量相关性的热平均值。

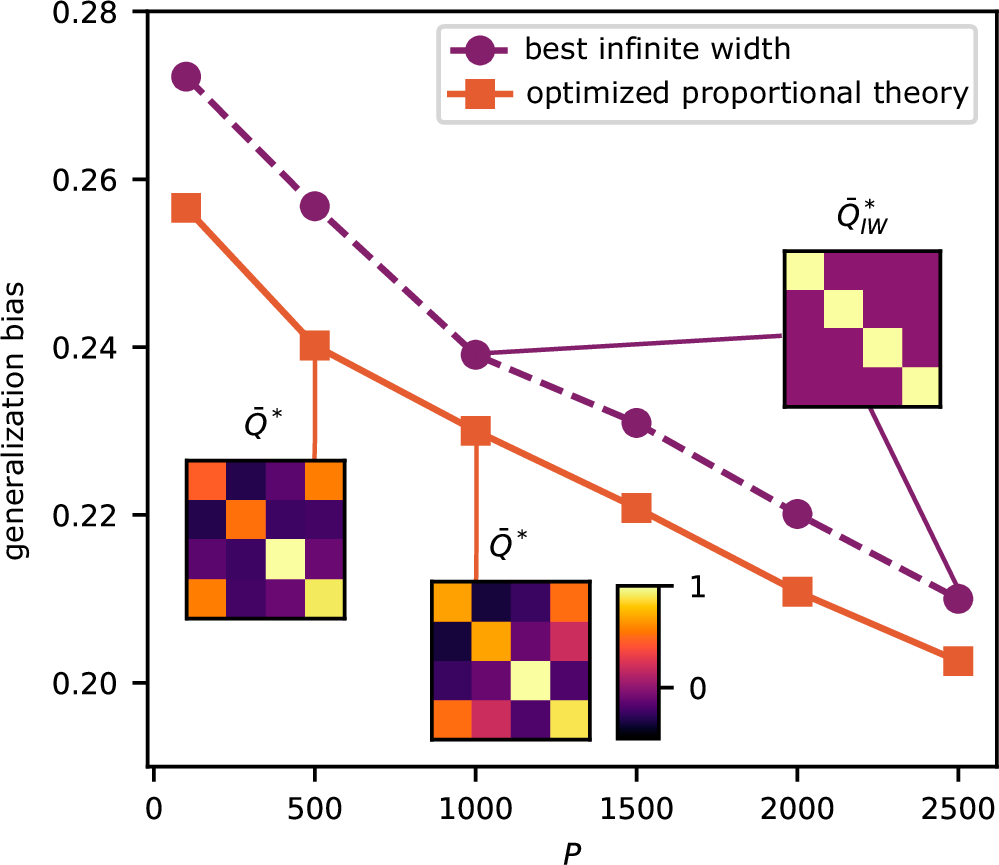
论文观察结果并不排除全连接深度神经网络架构中所有其他可能的特征学习形式：如无限宽内核的重整化并不是特征学习的唯一可能来源。与无限宽度限制无关的高阶核可能在特征学习中发挥作用，尤其是在考虑数据集大小 P 大致与全连接深度神经网络的参数数量 ∼ L × N²（Nℓ = N  ∀ ℓ）成比例的情况下。

关于重整化作为深度神经网络学习机制，笔者过去探讨过很多。

神经网络中的尺度重整化

在漂亮国的核潜艇与深度学习的内卷一文中，笔者总结过：玻尔兹曼机践行了重整化群的思想，事实上，在神经网络中引入隐含节点就是尺度重整化。每一次尺度变换后，自由能保持不变。F =-lnZ,  这里Z是配分函数，是一个能量（不同能级上粒子数）的概率分布，Z不变，即能量的概率分布不变。重整化群给出了损失函数，也就是不同层的F自由能的差异，或者说两个能量概率分布的“距离”， 训练就是来最小化这个距离。

笔者在相变与涌现中特别介绍了重整化群：重整化群（RG : Renormalization Group) 是研究不同尺度下对称性破缺与重建过程的核心数学手段。借助重整化群这一研究复杂物理系统行为的框架，人们可以在不同尺度上分析系统，并理解随着观察尺度的变化，系统的特性如何变化。通过这种方式，RG提供了一种研究微观细节如何产生较大尺度新涌现特性的方法。

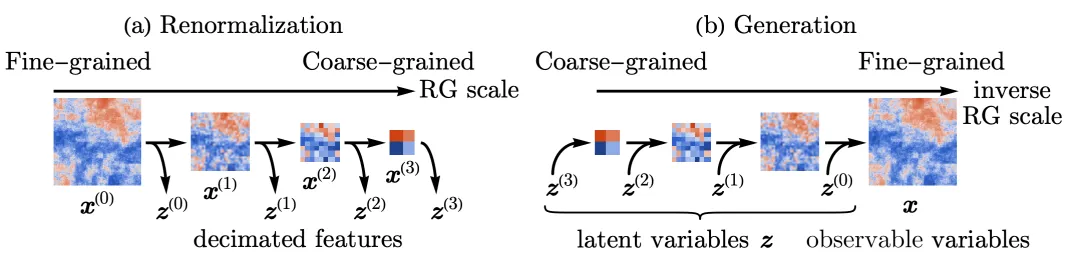
然后又在​重整化群与生成式AI文中详述了重整化群流在预训练与生成方面的机理：对一张图像，重整化从细颗粒度到粗颗粒度，逐层提取潜变量Zn, 提取图像中蕴含的各层次的结构；而生成图像的过程就是从粗粒度，对潜变量的高斯概率分布进行采样，重建下一个层次的结构（类似你跟别人描述这个人浓眉大眼）。重整化的群变换Gn 在生成过程中用到 Gn的逆。GPT 和其他大语言模型的使用的Transformer其实就可以类比这些重整化的群变换G。

重整化与大模型数理机制

物理诺奖、统计力学与大模型，笔者断言：Transformer 等价于重整化，基于过去对这一领域的关键分析： 重整化（RG）包括一个由大量自由度描述的系统，RG逐级尺度执行粗粒度化操作，自由度子集被组合在一起平均，以形成新的集体变量/隐变量。重整化自然成为统计力学的最佳工具。

重整化群与生成式AI 中，RG的数学形式表达为：G(Z) = G1G2G3G…Gn( Z )。这里的G1到Gn对应不同层次上Operation 或者说Transformation，也就是在各个层次的潜变量构成的新坐标系里面的变换，Gx(Z)是系统在潜变量函数基张成的空间中的样子。

重整化群流作为最优输运 不仅确定了精确重整化群流的方程等效于场的相对熵的最优输运梯度流，还巧妙的使用最优输运的思想将重整化群转化为变分问题。

尺度变换的每一步，RG 流都将会沿着最优输运的方向进行，也就是物理量的 RG 流尺度变换前的概率分布与尺度变换后的概率分布的距离最近的方向，而最优输运某种意义上是自然演化的必然方向和准则。

图片

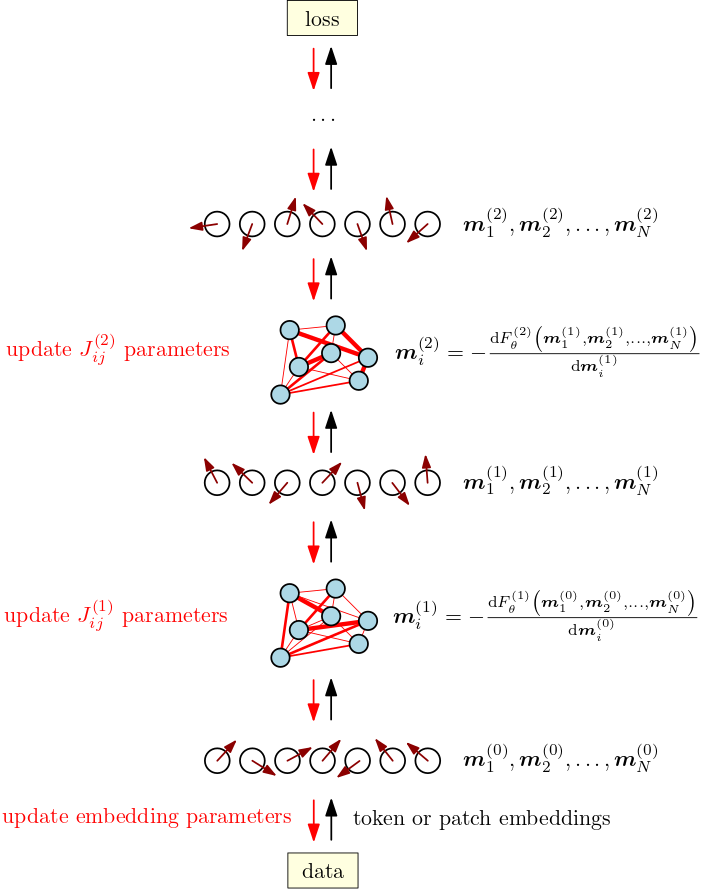
笔者在降低大模型幻觉的必由之路文中针对重整化、范畴与transformer之间的关系做了详细的阐述：

重整化本质是尺度从小到大粗粒度化概率分布的过程，而深度神经网络擅长学习小尺度结构逐级到认知全局特征，而大模型的Transformer 则可以逆重整化流，逐尺度重建微观概率分布，从而完成生成。

这里的范畴是Transformer视角下的高维概率向量编织起来的事物之间的各种复杂的关系。从海量的预训练数据集中提纯出来，对大量的分段线性核函数参数化后的表达。这些关系，关系的关系，关系的关系的关系，本质上，在范畴论概念下，就是对事物的米田嵌入。

重整化视角的大模型数理认知框架

MIT对大模型数理原理的强有力证明，笔者做了重整化视角的大模型数理认知框架原理回顾：

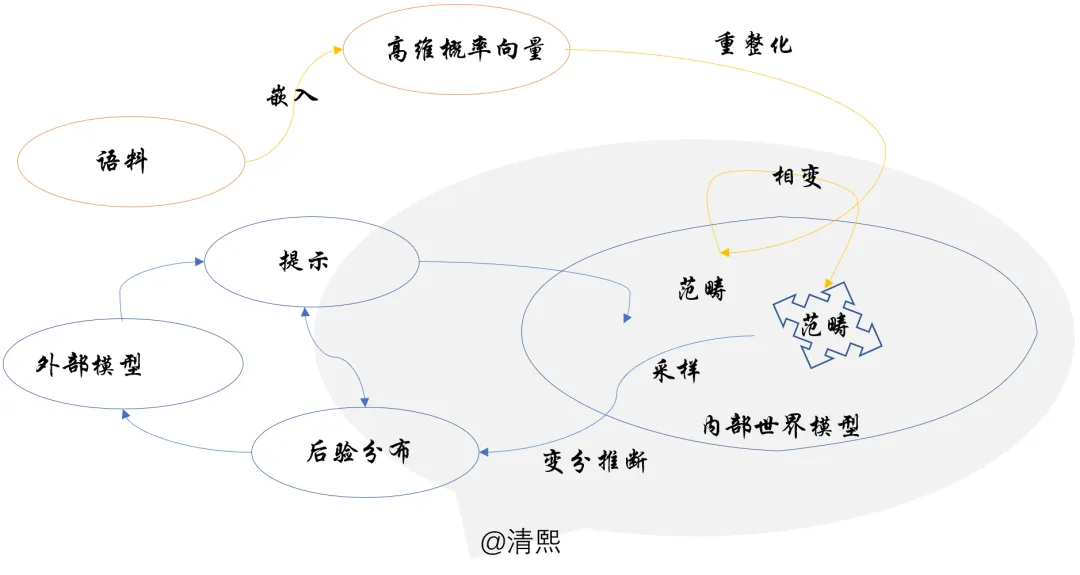
海量的文本或者多模态语料组成了大模型需要认知的外部世界的基本信息；嵌入构建高维概率化的语言空间，用来建模语言文字图像以及音视频，并对连续变量做离散化；

预训练以重整化群流的方式进行，在不同尺度上提炼语料数据中的信息概率分布；重整化群流的每一步流动（自回归预测逼近训练语料概率分布），都沿着最优输运的成本最低方向进行；

重整化群在不动点附近因新语料带来微扰而发生对称性破缺，滑入不同的相空间；不同的相空间，对应某种意义上的范畴，可形象化为信息的结晶；这是大模型从语料中学到的内部世界模型；

在外部感官输入下（被提示置于某种上下文），大模型内部将限定在相应的高维语言概率空间的子空间内推理；推理是在子空间中采样，类比时跨范畴采样；

采样不断进行，基于内部概率化了的世界模型（预训练获得的先验），针对感官输入（提示），做变分推断，最小化自由能，获取最佳采样分布q*，作为对导致感官输入的外部后验的预测。

图片

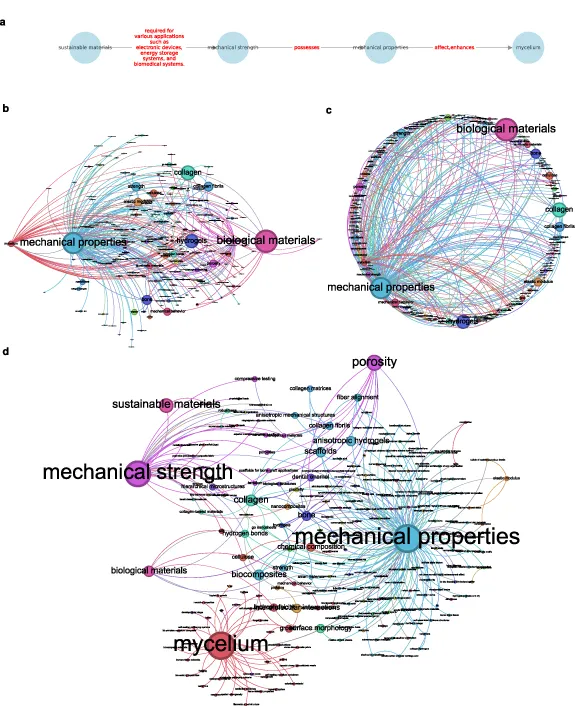
可总结为：1、重整化从海量语料中提取出范畴，2、持续重整化驱动范畴解构重组结晶，3、生成过程于范畴中采样做变分推理。

推演大模型局限与发展脉络，笔者基于这个数理认知框架推断：采样做变分推理的部分尤其薄弱，即使学到某些领域的丰富的知识，提炼成相当丰富的范畴，其采样与变分推理还处在早期人工智能“炼丹”阶段，提示工程、CoT、o1的强化学习推理，仅是“炼丹”方式不同。

通往ASI的大模型推理

重新思考 MoE中笔者看到大模型不断提升推理能力的路径：“目前 MoE 可以理解为一种分布式采样策略，可以GShard硬编码，或进一步DeepSeekMoE细分，也可以如MoDE基于噪声更灵活调节策略，亦或引入某种优化器(类似SQL优化器)，并最终依赖推理的scaling law涌现出策略”。

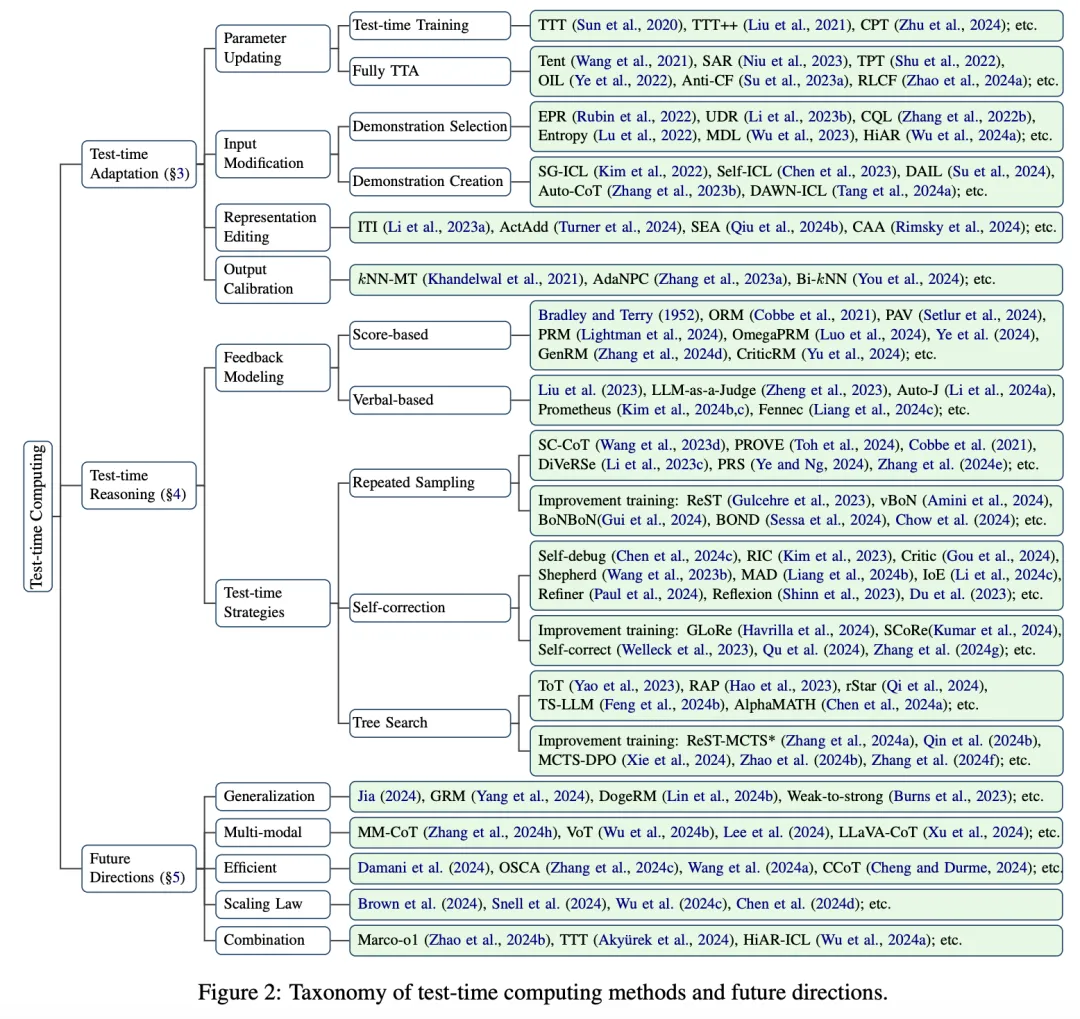
测试时计算（Test-time Computing）也被寄予厚望。【文献2】苏州大学、新加坡国立大学和蚂蚁集团的研究人员探索了测试时计算，追踪了其从 System-1 到 System-2 模型的演变。

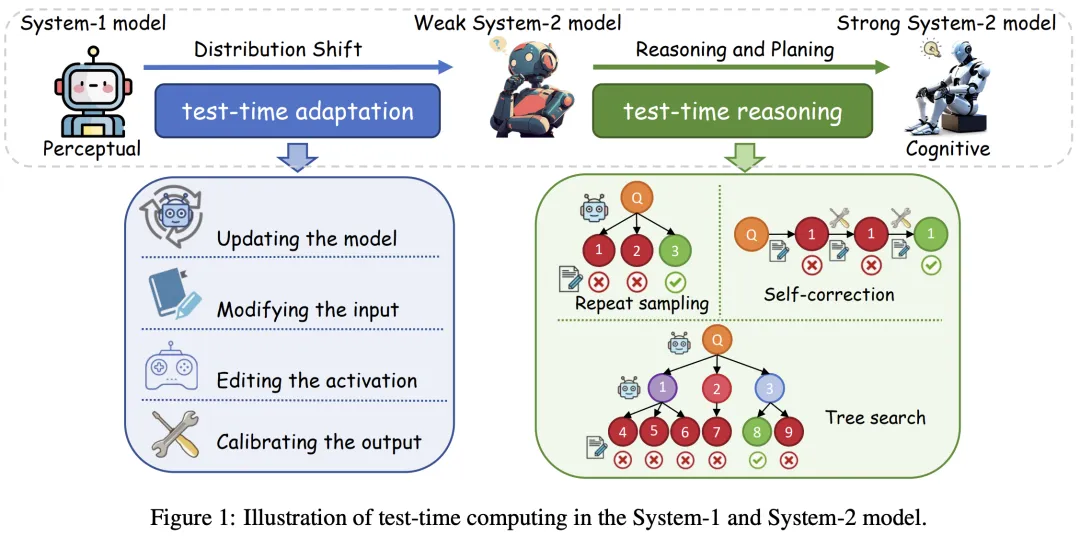
测试时计算最初应用于 System-1 模型，通过参数更新、输入修改和输出校准来解决分布偏移并增强稳健性，现在使用重复采样、自我校正和树搜索等策略加强了 System-2 模型中的推理。

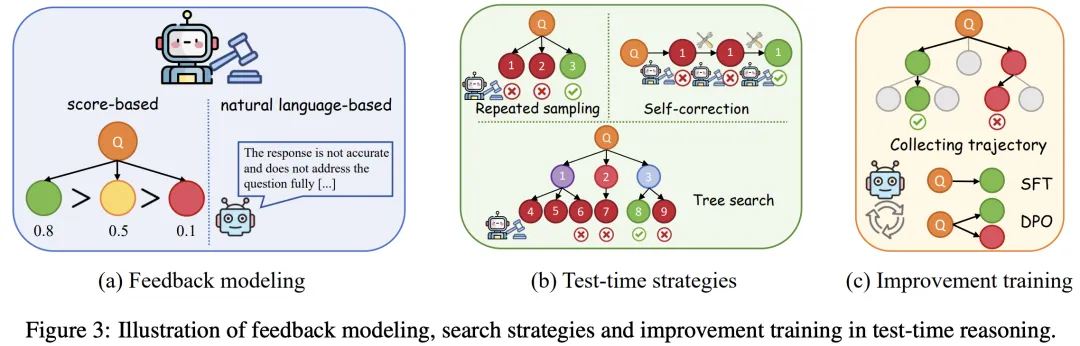
测试时适应（TTA）在推理过程中使用测试样本信息微调模型。关键考虑因素包括学习信号、参数更新和确保效率。测试时训练 （TTT） 学习信号使用辅助任务，而完全测试时适应 （FTTA） 利用内部反馈（如熵最小化）。

笔者认为，测试时计算模型更新，等于利用测试样本信息在推理阶段进一步微调了模型参数，使模型能够适应测试分布。这样不仅学了更多的内容（测试语料），还反复推敲学习如何采样变分用于推理，本质是积累了推理的范畴。

测试时计算的训练方式，如果推广到更大范围的语料（甚至重复利用预训练时期的语料），可以积累更多推理范畴，从而提升推理能力。预训练的语料中，也有大量类似的推理场景，针对此类场景，采用测试时适应，或类似的测试时计算的策略，在预训练时就可以同时积累推理的范畴，即推理内化成内部世界模型中的一部分。

文献1，https://www.nature.com/articles/s41467-024-55229-3   Local kernel renormalization as a mechanism for feature learning in overparametrized convolutional neural networks

文献 2， https://arxiv.org/abs/2501.02497  Test-time Computing: from System-1 Thinking to System-2 Thinking

本文转载自​​清熙​​，作者： 王庆法 ​​​​