LLM架构从基础到精通之门控循环单元(GRUs)
在之前对循环神经网络(RNNs)和长短期记忆网络(LSTMs)的深入探讨中,我们了解了它们在处理序列数据方面的强大能力以及应对挑战的独特方式。接下来,我们将聚焦于另一种重要的神经网络架构——门控循环单元(GRUs),它在解决标准 RNN 面临的问题上展现出了独特的优势。
12. 门控循环单元(GRUs)
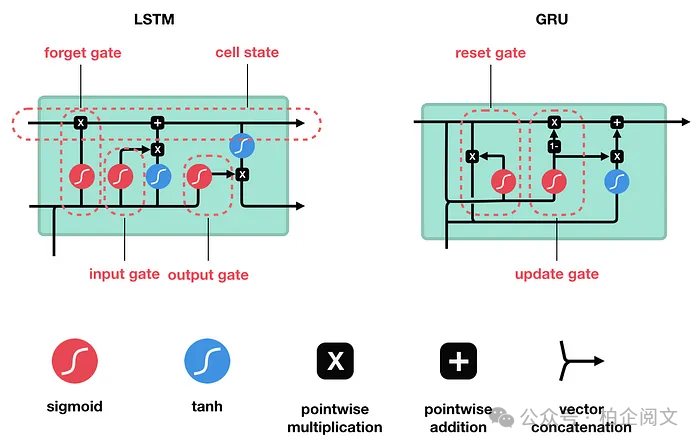
门控循环单元(GRU)由 Cho 等人在 2014 年提出,旨在解决标准循环神经网络(RNN)面临的梯度消失问题。GRU 与长短期记忆网络(LSTM)有许多共同之处,这两种算法都使用门控机制来控制记忆过程。
想象一下,你试图通过反复听一首歌来学习它。一个基本的 RNN 可能在听到结尾时就忘记了歌曲的开头。GRU 通过使用门来控制哪些信息被记住、哪些信息被遗忘,从而解决了这个问题。
GRU 通过将输入门和遗忘门合并为一个单一的更新门,并添加一个重置门,简化了长短期记忆网络的结构。这使得它们训练速度更快,使用更方便,同时仍然能够长时间记住重要信息。
更新门:这个门决定了过去的信息中有多少应该被传递到未来。
重置门:这个门确定了过去的信息中有多少需要被忽略。
这些门帮助 GRU 在记住重要细节和忘记不重要的信息之间保持平衡,就像你在听歌曲时可能会专注于记住旋律而忽略背景噪音一样。
GRU 非常适合处理序列数据的任务,如预测股票市场、理解语言,甚至生成音乐。它们可以通过跟踪过去的信息并利用这些信息进行更好的预测来学习数据中的模式。这使得它们在任何需要理解先前数据点上下文的应用中都非常有用。
12.1 与 LSTMs 和普通 RNNs 的比较
为了理解 GRU 的适用场景,让我们将它们与 LSTMs 和普通 RNNs 进行比较。
普通 RNNs:可以将普通 RNNs 视为循环神经网络的基本版本。它们通过将信息从一个时间步传递到下一个时间步来工作,就像接力赛中每个赛跑者将接力棒传递给下一个人一样。然而,它们有一个很大的缺陷:在长序列中它们往往会忘记信息。这是由于梯度消失问题,这使得它们难以学习数据中的长期依赖关系。
LSTMs:长短期记忆网络旨在解决这个问题。它们使用更复杂的结构,包含三种类型的门:输入门、遗忘门和输出门。这些门就像一个复杂的文件系统,决定哪些信息要保留、哪些信息要更新、哪些信息要丢弃。这使得 LSTMs 能够长时间记住重要信息,使它们非常适合处理需要跨多个时间步的上下文的任务,如理解文本段落或识别长时间序列中的模式。
GRUs:门控循环单元是 LSTMs 的简化版本。它们通过将输入门和遗忘门合并为一个单一的更新门,并添加一个重置门来简化结构。这使得 GRUs 比 LSTMs 计算强度更低,训练速度更快,同时仍然能够有效地处理长期依赖关系。
12.2 是什么使 GRU 比传统 RNN 更特殊和有效?
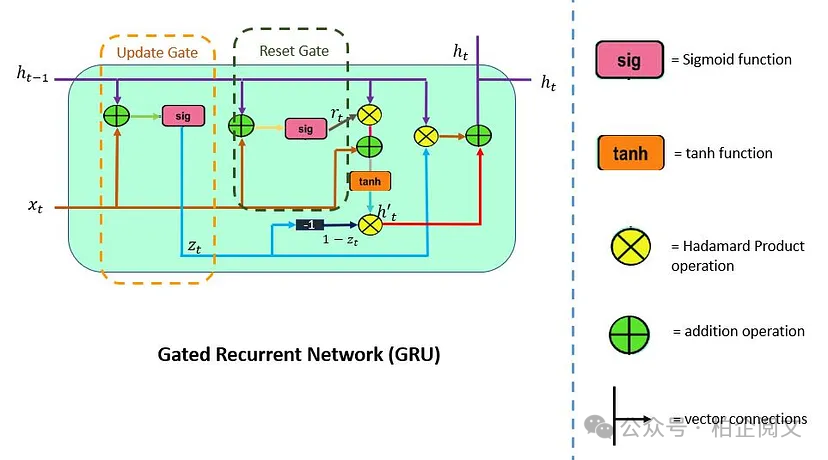
GRU 支持门控和隐藏状态来控制信息的流动。为了解决 RNN 中出现的问题,GRU 使用两个门:更新门和重置门。
你可以将它们视为两个向量条目(0,1),可以执行凸组合。这些组合决定了哪些隐藏状态信息应该被更新(传递)或在需要时重置隐藏状态。同样,网络学会跳过不相关的临时观察。
LSTM 由三个门组成:输入门、遗忘门和输出门。与 LSTM 不同,GRU 没有输出门,并且将输入门和遗忘门合并为一个单一的更新门。
接下来,让我们更详细地了解更新门和重置门。
12.2.1 更新门
更新门()负责确定需要传递到下一个状态的先前信息(先前时间步)的数量。它是一个重要的单元。下面的示意图展示了更新门的结构。
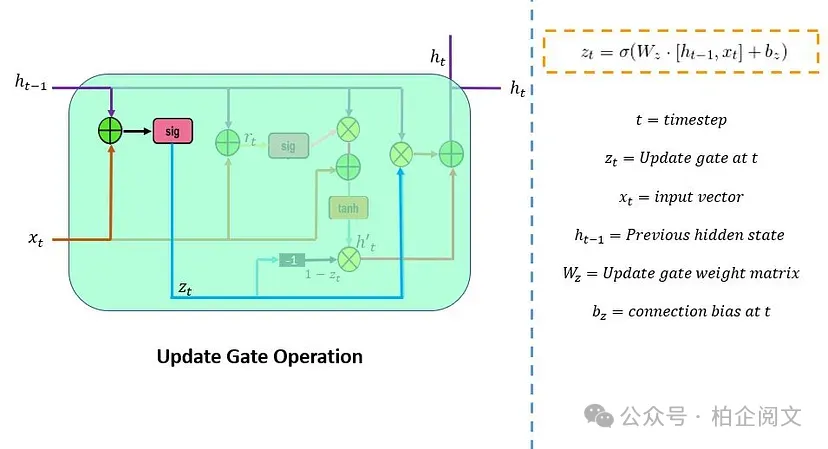
这里, 是网络单元中的输入向量,它与参数权重()矩阵相乘。 中的 表示它保存了前一个单元的信息,并与它的权重相乘。接下来,将这些参数的值相加,并通过 sigmoid 激活函数。在这里,sigmoid 函数将生成介于 0 和 1 之间的值。
12.2.2 重置门
重置门()用于决定需要忽略多少过去的信息。其公式与更新门相同,但它们的权重和门的使用方式有所不同。下面的示意图表示了重置门。
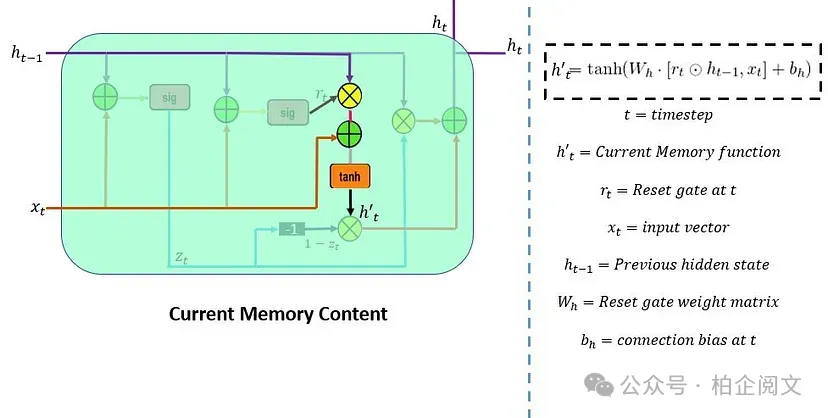
有两个输入, 和 。将它们与各自的权重相乘,进行逐点相加,并通过 sigmoid 函数。
13. 门的作用

14. 简单 GRU 的实现
为了强化我们所涵盖的概念,让我们通过实践,在 Python 中从头开始实现一个基本的门控循环单元(GRU)。
下面的代码片段展示了一个简化的 GRU 类,突出了 GRU 架构中前向和后向传播的基本功能。
import numpy as np
class SimpleGRU:
def __init__(self, input_size, hidden_size, output_size):
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.W_z = np.random.randn(hidden_size, input_size)
self.U_z = np.random.randn(hidden_size, hidden_size)
self.b_z = np.zeros((hidden_size, 1))
self.W_r = np.random.randn(hidden_size, input_size)
self.U_r = np.random.randn(hidden_size, hidden_size)
self.b_r = np.zeros((hidden_size, 1))
self.W_h = np.random.randn(hidden_size, input_size)
self.U_h = np.random.randn(hidden_size, hidden_size)
self.b_h = np.zeros((hidden_size, 1))
self.W_y = np.random.randn(output_size, hidden_size)
self.b_y = np.zeros((output_size, 1))
def sigmoid(self, x):
return1 / (1 + np.exp(-x))
def tanh(self, x):
return np.tanh(x)
def softmax(self, x):
exp_x = np.exp(x - np.max(x))
return exp_x / exp_x.sum(axis=0, keepdims=True)
def forward(self, x):
T = len(x)
h = np.zeros((self.hidden_size, 1))
y_list = []
for t in range(T):
x_t = x[t].reshape(-1, 1)
z = self.sigmoid(np.dot(self.W_z, x_t) + np.dot(self.U_z, h) + self.b_z)
r = self.sigmoid(np.dot(self.W_r, x_t) + np.dot(self.U_r, h) + self.b_r)
h_tilde = self.tanh(np.dot(self.W_h, x_t) + np.dot(self.U_h, r * h) + self.b_h)
h = (1 - z) * h + z * h_tilde
y = np.dot(self.W_y, h) + self.b_y
y_list.append(y)
return y_list
def backward(self, x, y_list, target):
T = len(x)
dW_z = np.zeros_like(self.W_z)
dU_z = np.zeros_like(self.U_z)
db_z = np.zeros_like(self.b_z)
dW_r = np.zeros_like(self.W_r)
dU_r = np.zeros_like(self.U_r)
db_r = np.zeros_like(self.b_r)
dW_h = np.zeros_like(self.W_h)
dU_h = np.zeros_like(self.U_h)
db_h = np.zeros_like(self.b_h)
dW_y = np.zeros_like(self.W_y)
db_y = np.zeros_like(self.b_y)
dh_next = np.zeros_like(y_list[0])
for t in reversed(range(T)):
dy = y_list[t] - target[t]
dW_y += np.dot(dy, np.transpose(h))
db_y += dy
dh = np.dot(np.transpose(self.W_y), dy) + dh_next
dh_tilde = dh * (1 - self.sigmoid(np.dot(self.W_z, x[t].reshape(-1, 1)) + np.dot(self.U_z, h) + self.b_z))
dW_h += np.dot(dh_tilde, np.transpose(x[t].reshape(1, -1)))
db_h += dh_tilde
dr = np.dot(np.transpose(self.W_h), dh_tilde)
dU_h += np.dot(dr * h * (1 - self.tanh(np.dot(self.W_h, x[t].reshape(-1, 1)) + np.dot(self.U_h, r * h) + self.b_h)), np.transpose(h))
dW_h += np.dot(dr * h * (1 - self.tanh(np.dot(self.W_h, x[t].reshape(-1, 1)) + np.dot(self.U_h, r * h) + self.b_h)), np.transpose(x[t].respose(1, -1)))
db_h += dr * h * (1 - self.tanh(np.dot(self.W_h, x[t].reshape(-1, 1)) + np.dot(self.U_h, r * h) + self.b_h))
dz = np.dot(np.transpose(self.U_r), dr * h * (self.tanh(np.dot(self.W_h, x[t].reshape(-1, 1)) + np.dot(self.U_h, r * h) + self.b_h) - h_tilde))
dU_z += np.dot(dz * h * z * (1 - z), np.transpose(h))
dW_z += np.dot(dz * h * z * (1 - z), np.transpose(x[t].reshape(1, -1)))
db_z += dz * h * z * (1 - z)
dh_next = np.dot(np.transpose(self.U_z), dz * h * z * (1 - z))
return dW_z, dU_z, db_z, dW_r, dU_r, db_r, dW_h, dU_h, db_h, dW_y, db_y
def update_parameters(self, dW_z, dU_z, db_z, dW_r, dU_r, db_r, dW_h, dU_h, db_h, dW_y, db_y, learning_rate):
self.W_z -= learning_rate * dW_z
self.U_z -= learning_rate * dU_z
self.b_z -= learning_rate * db_z
self.W_r -= learning_rate * dW_r
self.U_r -= learning_rate * dU_r
self.b_r -= learning_rate * db_r
self.W_h -= learning_rate * dW_h
self.U_h -= learning_rate * dU_h
self.b_h -= learning_rate * db_h
self.W_y -= learning_rate * dW_y
self.b_y -= learning_rate * db_y在上述实现中,我们引入了一个简化的 SimpleGRU 类,以展示 GRU 的核心机制。示例用法演示了如何初始化 GRU、创建输入序列和目标输出的随机数据、执行前向和后向传播,以及随后使用计算出的梯度更新权重和偏差。
14.1 GRUs 的优缺点
GRUs 的优点
- 序列数据建模:GRUs 在处理序列方面表现出色,非常适合语言处理、语音识别和时间序列分析等任务。
- 可变长度输入:GRUs 可以处理不同长度的序列,适用于输入大小不同的应用场景。
- 计算效率高:与更复杂的循环架构(如 LSTMs)相比,由于其更简单的设计,GRUs 在计算上更高效。
- 缓解梯度消失:GRUs 比传统 RNNs 更有效地解决了梯度消失问题,能够捕获数据中的长期依赖关系。
GRUs 的局限性
- 长期记忆有限:虽然 GRUs 在捕获长期依赖关系方面比标准 RNNs 更好,但对于具有复杂依赖关系的非常长的序列,它们可能不如 LSTMs 有效。
- 表达能力较弱:在某些情况下,GRUs 可能无法像 LSTMs 那样有效地捕获复杂的模式,特别是在对高度复杂的序列进行建模时。
- 特定应用:对于需要显式内存控制或复杂上下文建模的任务,LSTMs 或更高级的架构可能更合适。
14.2 在 GRUs 和 LSTMs 之间选择
选择使用门控循环单元(GRUs)还是长短期记忆(LSTM)网络取决于你的具体问题和数据集。以下是一些考虑因素:
使用 GRUs 的情况:
- 计算资源有限:与 LSTMs 相比,GRUs 的计算强度较低,在资源受限的情况下是首选。
- 简单性重要:如果你想要一个更简单的模型,同时仍然能够合理地捕获序列依赖关系,GRUs 是一个不错的选择。
- 较短序列:对于涉及较短依赖关系的序列任务,GRUs 可以提供足够的性能,而无需 LSTM 的复杂内存管理。
使用 LSTMs 的情况:
- 捕获长期依赖关系:LSTMs 更适合于捕获长程依赖关系至关重要的任务,如语言建模、语音识别和某些时间序列预测。
- 精细的内存控制:LSTMs 提供了对内存的更明确控制,在需要精确内存处理时是更好的选择。
- 复杂序列:如果你的数据呈现出复杂的序列模式和依赖关系,LSTMs 通常在建模这些复杂性方面更有效。
在实践中,最好在你的特定任务上对 GRUs 和 LSTMs 进行实验,以确定哪种架构性能更好。有时,两者之间的选择取决于对数据集的实证测试和验证。
15. 结论
我们深入探讨了循环神经网络(RNNs),详细研究了它们的核心机制、训练挑战以及提高性能的高级设计。以下是一个简要概述:
我们剖析了 RNNs 的结构,强调了它们通过内部记忆状态处理序列的能力。讨论了关键过程,如前向传播和时间反向传播(BPTT),解释了 RNNs 如何处理序列数据。
我们还强调了主要的训练挑战,包括梯度消失和爆炸,这些问题可能会干扰学习。为了解决这些问题,我们探索了诸如梯度裁剪和初始化策略等解决方案,这些方案有助于稳定训练并提高网络从较长序列中学习的能力。
门控循环单元(GRUs)是 RNNs 的一种强大变体,专为高效处理序列数据而设计。它们有效地缓解了梯度消失等问题,并擅长捕获序列中的依赖关系,使其非常适合自然语言处理、语音识别和时间序列分析等任务。
GRUs 使用门控机制来控制信息的流动,使其能够在保持计算效率的同时捕获长期依赖关系。理解 GRUs 背后的架构和数学原理是在机器学习任务中有效利用它们的关键。
在选择 GRUs 和 LSTMs 时,需要考虑多个因素,包括数据复杂性、计算资源和要建模的依赖关系的长度。这两种架构都有其优缺点,因此最佳选择取决于任务的具体要求。
本文转载自 柏企阅文,作者: 柏企
















