人工智能小白到高手：什么是损失函数

在机器学习中，损失函数是用来衡量模型预测值与真实值之间差距的一个函数。它在模型训练过程中起着至关重要的作用，因为通过最小化损失函数，模型能够调整其参数，从而使得预测结果越来越接近真实值。

为了帮助理解这一点，我们将以均方误差（MSE）为例，详细讲解什么是损失函数，以及它在实际应用中的作用。

什么是损失函数？ 

损失函数是一个用于评估模型预测准确性的数学函数。具体来说，损失函数通过对比模型的预测值与真实值，计算出一个数值（损失），这个数值代表了模型预测的误差。

如果损失较大，意味着模型的预测值与真实值相差较远；如果损失较小，说明模型的预测已经较为精确。

在一个预测问题中，假设我们有：

在下图中，您可以将损失可视化为从数据点指向模型的箭头。箭头表示模型的预测结果与实际值之间的差距。

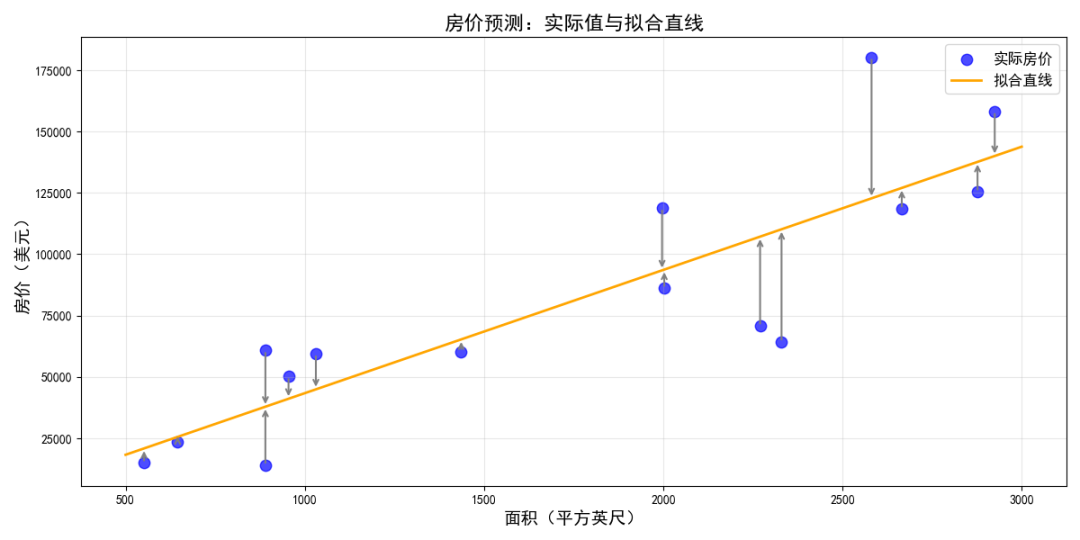
在统计学和机器学习中，损失函数用于衡量预测值与实际值之间的差异。损失函数侧重于值之间的距离，而不是方向。

例如，如果模型预测值为 2，但实际值为 5，我们并不关心损失为负值 −3（2−5=−3）。我们关心的是这两个值之间的距离为 3。

因此，所有用于计算损失的方法都会移除符号。

移除此符号的两种最常用方法如下：

• 计算实际值与预测值之间的差值的绝对值。
• 将实际值与预测值之间的差值平方。

均方误差（MSE）

以回归任务为例，均方误差（MSE）是最常见的损失函数之一。

它衡量的是预测值与真实值之间差距的平方的平均值。

均方误差的优点是，它对大误差非常敏感，因此可以较好地惩罚那些错误较大的预测。MSE是连续型数值任务中常用的损失函数，尤其在模型希望尽量减少预测误差时特别有效。

为什么需要损失函数？ 

损失函数的作用可以通过一个简单的例子来理解。假设我们正在使用线性回归模型来预测房价，给定某些特征（如面积），模型预测出一个价格，而实际的房价是已知的。

损失函数将计算预测值与真实值之间的差距，具体来说，均方误差（MSE）将计算每个预测值与真实值之间的差异，然后求出这些差异的平方和的平均值。

通过最小化这个损失函数，模型能够学习到如何调整其参数，使得预测的房价尽可能接近实际房价。

例如，如果模型的预测差异过大（例如，预测的价格比实际价格高出很多），均方误差就会较大，模型将意识到它需要进行调整，以减少这种差距。

如何使用损失函数进行优化？ 

训练机器学习模型时，我们的目标是最小化损失函数。最常见的方法是使用梯度下降算法。梯度下降通过不断调整模型的参数，使得损失函数的值逐步减小，从而提升模型的预测能力。

在均方误差的情况下，我们通过计算损失函数对每个模型参数的梯度（即偏导数），来决定如何调整参数。通过反复进行这一过程，损失函数的值会逐渐减少，模型的预测能力也会逐步增强。

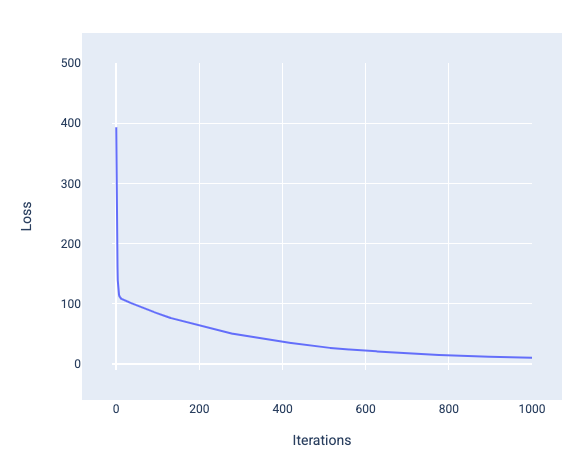
损失曲线，显示模型在第 1000 次迭代左右收敛。

损失函数的选择与优化 

选择合适的损失函数是成功训练模型的关键。不同任务可能需要不同的损失函数。

例如，在回归任务中，均方误差（MSE）是一种常用的选择，但在一些特定场景下，如数据中包含大量异常值时，可能需要使用其他损失函数，如平均绝对误差（MAE）或者Huber损失，它们对异常值更为鲁棒。

此外，损失函数的优化也很重要。在使用MSE时，确保数据进行适当的归一化或标准化，以防止过大的输入值导致训练不稳定。合理的学习率选择、优化器的使用（如Adam或SGD）等因素，也都将影响损失函数的最小化过程。

总结 

通过均方误差（MSE）这一具体例子，了解了什么是损失函数，损失函数如何在机器学习模型中评估预测的准确性，并推动模型优化。

损失函数通过量化模型的预测误差，为模型提供了学习的反馈，帮助模型在训练过程中逐步调整参数以达到更好的预测效果。理解损失函数的本质和应用，对于构建有效的机器学习模型至关重要。

本文转载自 ​​AI取经路​​，作者： AI取经路