在离散域上求解抛物线偏微分方程的框架

最优传输距离数值求解

拉格朗日成本下的神经最优传输 一文中，笔者整理了三个要点：

1.最优传输距离（也称推土距离）将统一深度学习概率分布距离计算

2.大模型Transformer等价的重整化群流都将会沿着最优传输的方向进行

3.拉格朗日成本处理神经网络最优传输能更有效地建模复杂的系统动力学

文章提到最优传输距离目前受到数值计算效率的制约，影响了其广泛应用。这也是笔者一直关注的方向之一。

文中介绍的纽约大学和Meta的AI学者创新的拉格朗日成本处理神经网络最优传输的方法，能更有效地解决最优传输复杂成本函数问题。

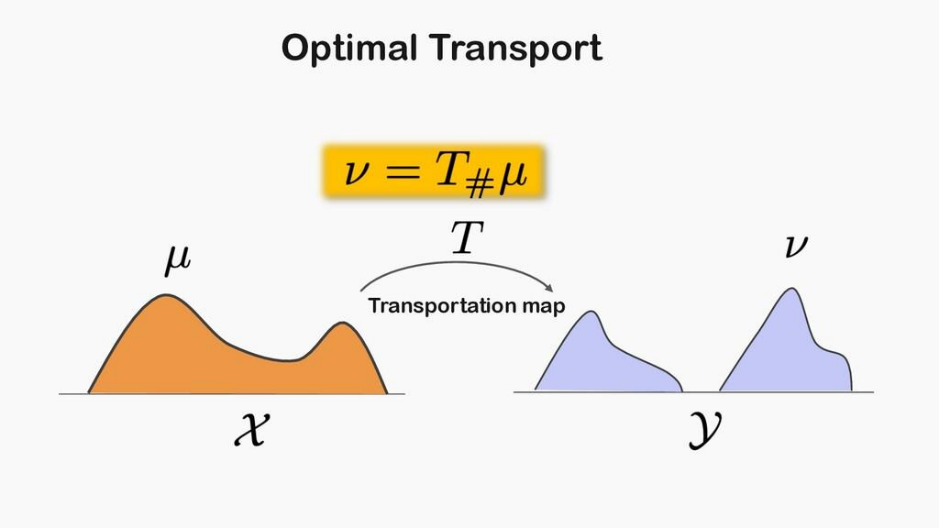
我们知道，最优传输问题大致上是寻求以最低的成本将所有质量从源分布传输到目标分布。

众多学者在这个领域做出了建设性的进展：熵正则化近似提供了一种解决各种最优传输问题的方法，如著名的Sinkhorn算法。

核心思想是在目标函数上加入熵正则化项，把复杂边际的线性规划问题转化为平滑可行域上的求解过程。  

有学者进一步扩展Sinkhorn 算法，证明二阶Wasserstein 距离的核可以用热核（Heat kernel）近似，从而能够利用几何域上的 PDE（Partial Differential Equations 偏微分方程） 求解技术进行计算。

麻省理工学院开发了一种新算法，在几何域上利用热核近似，求解某个二阶抛物线非线性偏微分方程，可以克服Sinkhorn算法中常见的小熵系数带来的数值挑战【文献1】。

这个算法具备足够的通用性，可以数值求解一类典型的二阶抛物线偏微分方程，最优传输之外，还有例如著名的热扩散、Hamilton-Jacobi、Fokker-Planck等方程。学者们称之为：求解抛物线偏微分方程的框架。

求解抛物线偏微分方程的框架

最近爆火的《黑神话-悟空》等视频游戏和电影中，创建模拟火焰等物理现象的视觉效果，以及使用 3D 打印等工具制造复杂的几何形状，后台很大程度上依赖偏微分方程对这些自然过程进行建模。

偏微分方程分析自然成为计算机图形学、几何处理和邻近科技领域中无处不在的技术。特别是，抛物线偏微分方程描述的各种各样的现象：

Hamilton-Jacobi 方程的实例模拟了前沿传播的时间演变和经历非线性扩散的函数的演变。

Fokker-Planck 方程描述了由随机过程驱动的密度函数的演变。而著名热扩散方程，则预测热量如何随时间沿表面或体积扩散。

这都是历史悠久的方程，也包括计算机图形学中各种问题如火焰建模G方程、随机热核估计、内侧轴检测和纹理合成等等。

研究人员设计了许多算法来求解曲面上的这些问题，但他们的方法通常因为无法捕获无穷小或非线性现象，仅适用于线性问题或单个PDE。

一个有趣的例子是用于重心计算的卷积 Wasserstein 距离方法【文献2】：

在少量扩散的基础上，通过启发式方法来选择扩散时间，步长太小则数值不准，步长太大，则近似值出错。

上文提到的麻省理工学院开发的新算法则更通用，可以用于解决这一类非线性问题，通过将复杂的偏微分方程分解为更简单的问题来解决它们。

论文发表在 Transactions on Graphics 期刊和 SIGGRAPH 会议上。学者们称他们的主要贡献是：

一个数值框架，用于在弯曲三角形网格上求解线性和非线性抛物线偏微分方程，其效率与传统几何处理方法相当。

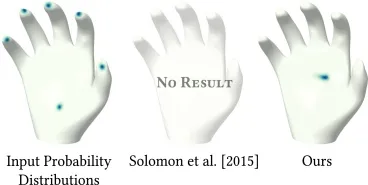
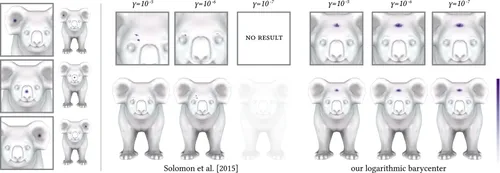
一种对数域扩散算法，克服了依赖于微量扩散的几何处理方法的已知局限性，在最佳输运（OT）任务中进行了演示。

一个对该数值框架在 G 方程数值积分方面的应用，该方程可以作为图形管道中的组件，用于模拟火和火焰。

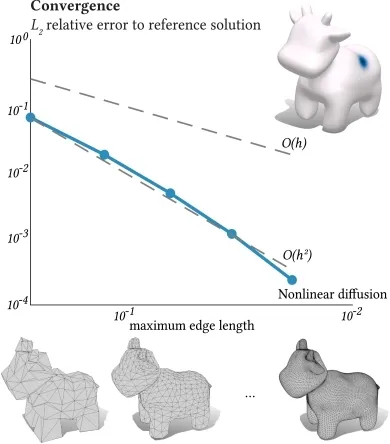
该算法通过将三角形网格上不同的非线性抛物线偏微分方程拆分为三个更简单的方程来求解，此框架可以帮助更好地分析形状并对复杂的动态过程进行建模。

G 方程在计算流体动力学 （CFD） 中广为人知，后作为“薄火焰模型”被引入计算机图形学界，用于模拟火和火焰，以及更广泛的燃烧现象。

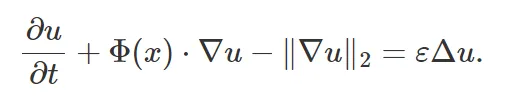
新框架实现了比标准方案更好的数值稳定性，且提供了匹配的数值结果，甚至精确解的合理近似值。 

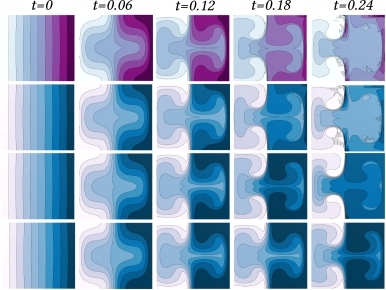
Fokker-Planck 方程是一个线性抛物线偏微分方程，描述了由随机微分方程 （SDE） 驱动的过程的概率密度函数的时间演变。

新框架可用于直接在弯曲三角形网格上求解 Fokker-Planck 方程。表明该框架为在传统几何处理中使用随机微分方程的新方法奠定了基础。

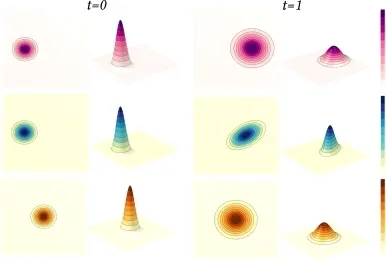
框架的典型应用案例

论文详述了该框架在Wasserstein 重心、测量插值、Fire 和 Flames 的数值积分三个领域的应用。以Wasserstein 重心计算为例：

“log-sum-exp” 技巧是一种用于稳定数值算法的标准方法，包括使用少量熵时的 Sinkhorn 算法。  

论文主张使用该数值框架直接在对数域中计算三角形网格上的热扩散结果，而不是在线性域中扩散，然后取对数，从而获得最优结果：

二阶抛物线 PDE 非常典型。该框架建立了一种有效的时间积分和空间离散化策略，以在三角形网格表面上的温和假设下求解这类偏微分方程。

微分方程与机器学习中提到，就像统计学家George Box 说的那样: 所有的模型都是错误的，但有一些是有用的。PDE对自然过程的建模无处不在。

今天初三刚开学的女儿一起散步时她说，其实世界就是个巨大的方程。

笔者一边在想这个认知自己是什么时候获得的，一边补充：这个巨大的方程可以用一个巨大的神经网络近似，这就是目前人工智能的核心。

而且我们能从世界中观测到的数据集决定了我们对世界认知的上限。“薛定谔的佛与深度学习中的因果“中笔者总结过：

最大似然事实上决定了模型可以学习到的极限，构成了所有学习方法的信息茧房。

【文献1】A Framework for Solving Parabolic Partial Differential Equations on Discrete Domains  https://dl.acm.org/doi/10.1145/3666087

【文献2】 Convolutional wasserstein distances: efficient optimal transportation on geometric domains ​ https://dl.acm.org/doi/10.1145/2766963           

本文转载自 ​​清熙​​，作者： 王庆法