大规模相似性搜索:原理、技术与 Faiss 实践
相似性搜索为何重要?
人工智能和机器学习的兴起,催生了大量高维数据表示形式,即嵌入(embeddings),它们捕捉数据点之间的复杂关系,助力强大的分析与理解。然而,在大型数据集中查找相似嵌入是一项计算密集型任务。相似性搜索在检索增强生成(Retrieval-Augmented Generation,RAG)领域引发了变革。RAG 将传统信息检索与语言模型相结合,通过利用相似性搜索查找相关文档,使模型能访问更广泛的知识库,生成更具信息量和上下文丰富的输出,从而提高生成文本的准确性和相关性。
大规模相似性搜索的挑战
传统数据库和搜索引擎难以满足大规模相似性搜索的需求。它们依赖结构化查询和索引方法,无法应对高维数据的动态特性。因此,需要专门的技术来解决这一问题。
Faiss 框架
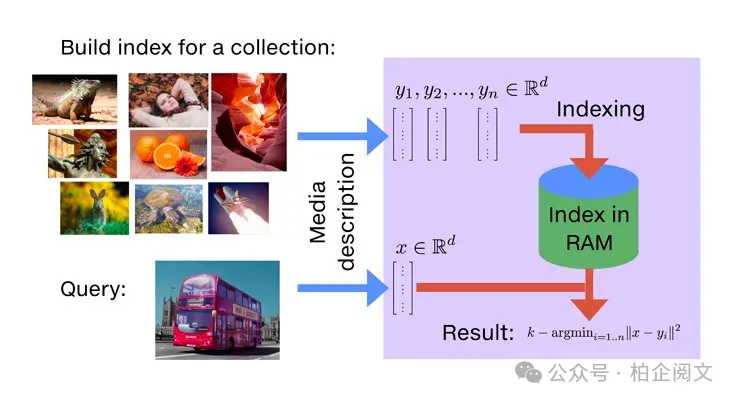
Faiss 由 Facebook AI Research 开发,是一个专为高效相似性搜索设计的强大库。它提供多种索引方法,在性能、准确性和内存使用之间进行了不同的权衡优化。Faiss 还支持 GPU 加速,非常适合处理大规模数据集。
基础准备
首先安装和导入必要的依赖项:
pip install faiss-cpu
import time
import faiss
import numpy as np接着定义一些常量:d 表示向量维度(128),nb 表示基础向量数量(10000),nq 表示查询向量数量(100)。
d = 128
nb = 10000
nq = 100为保证结果可复现,初始化随机种子:
np.random.seed(1234)生成两组随机向量,xb 代表基础向量(10000 x 128),xq 代表查询向量(100 x 128):
xb = np.random.random((nb, d)).astype('float32')
xq = np.random.random((nq, d)).astype('float32')这些向量本质上就是我们的数据点。
分层可导航小世界(Hierarchical Navigable Small World,HNSW)
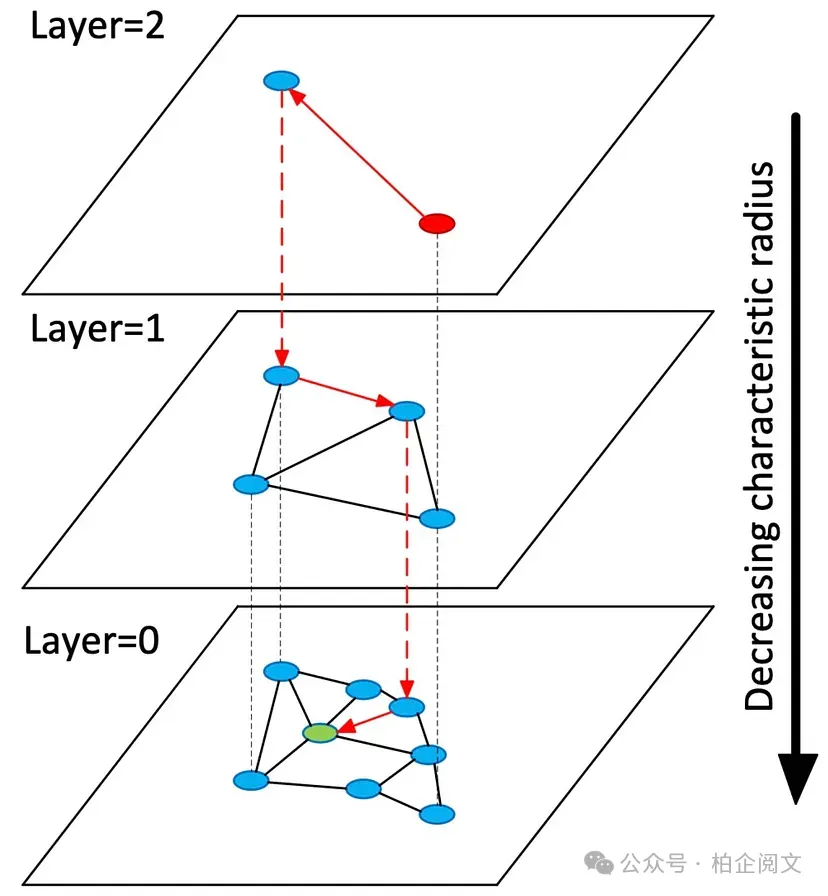
- 工作原理:HNSW 是一种基于图的索引方法,向量被组织在小世界图的层次结构中。图中的每个节点(向量)都与其最近邻节点相连。搜索时,算法在图中导航,快速收敛到最近的向量。
- 优势:HNSW 准确性高且搜索速度快,尤其适用于高维数据集。
- 关键参数:
M(每个节点的连接数):控制图中每个节点连接的邻居数量。数值越高,准确性越高,但内存消耗也越大。
efConstruction 和efSearch:分别控制索引构建和搜索过程中的探索深度。数值越高,搜索准确性越好,但计算量也更大。
创建两个 HNSW 索引 —— HNSWFlat 和 HNSWSQ(标量量化)来对比性能:
# HNSWFlat 是基本的 HNSW 实现
index_hnswflat = faiss.IndexHNSWFlat(d, 32)
start = time.time()
index_hnswflat.add(xb)
indexing_time_hnswflat = time.time() - start
start = time.time()
D, I = index_hnswflat.search(xq, 5)
search_time_hnswflat = time.time() - start
# HNSWSQ 结合了标量量化(SQ)以加快索引速度
quantizer_sq = faiss.IndexScalarQuantizer(d, faiss.ScalarQuantizer.QT_8bit)
index_hnswsq = faiss.IndexHNSWFlat(d, 32)
start = time.time()
index_hnswsq.add(xb)
indexing_time_hnswsq = time.time() - start
start = time.time()
D, I = index_hnswsq.search(xq, 5)
search_time_hnswsq = time.time() - start两个索引都使用“扁平”存储方法,即不压缩原始向量。
输出结果:
print(f"HNSWFlat Indexing Time: {indexing_time_hnswflat:.4f} seconds")
print(f"HNSWFlat Search Time: {search_time_hnswflat:.4f} seconds")
print(f"HNSWSQ Indexing Time: {indexing_time_hnswsq:.4f} seconds")
print(f"HNSWSQ Search Time: {search_time_hnswsq:.4f} seconds")与基于 IVF 的方法相比,HNSW 方法的索引速度明显较慢,因为 HNSW 需要构建邻居图,计算成本较高。由于标量量化(SQ)在索引过程中更紧凑地表示向量,降低了向量维度,所以 HNSWSQ 比 HNSWFlat 稍快。HNSWFlat 和 HNSWSQ 的搜索时间比基于 IVF 的方法略长,这是因为需要遍历图来找到最近邻居。HNSW 以高精度著称,尤其在高维空间中,但代价是索引和搜索时间较长。
倒排文件索引(Inverted File Index,IVF)

- 工作原理:IVF 是大规模数据集相似性搜索中另一种常用方法。它将数据集划分为多个桶(buckets)或“列表”,每次查询仅搜索其中一部分桶。
- 优势:与 HNSW 相比,IVF 的主要优势是内存需求较低。
- 关键参数:
nlist:聚类(或桶)的数量。数值越高,精度越高,但索引时间也会增加。
nprobe:查询时搜索的聚类数量。增加此参数可提高召回率,但会降低搜索速度。
对比 IndexIVFFlat(无乘积量化)和 IndexIVFPQ(有乘积量化):
# IVFFlat 使用无量化的扁平索引
nlist = 100
quantizer = faiss.IndexFlatL2(d)
index_ivfflat = faiss.IndexIVFFlat(quantizer, d, nlist, faiss.METRIC_L2)
start = time.time()
index_ivfflat.train(xb)
index_ivfflat.add(xb)
indexing_time_ivfflat = time.time() - start
index_ivfflat.nprobe = 10
start = time.time()
D, I = index_ivfflat.search(xq, 5)
search_time_ivfflat = time.time() - start
# IVFPQ 结合乘积量化(PQ)以提高内存效率
m = 8
nbits = 8
index_ivfpq = faiss.IndexIVFPQ(quantizer, d, nlist, m, nbits)
start = time.time()
index_ivfpq.train(xb)
index_ivfpq.add(xb)
indexing_time_ivfpq = time.time() - start
index_ivfpq.nprobe = 10
start = time.time()
D, I = index_ivfpq.search(xq, 5)
search_time_ivfpq = time.time() - startIVF 的关键思想是将数据集划分为聚类(桶),每次查询仅搜索其中一部分桶。这里设置 nlist 为 100,即有 100 个聚类。
输出结果:
print(f"IVFFlat Indexing Time: {indexing_time_ivfflat:.4f} seconds")
print(f"IVFFlat Search Time: {search_time_ivfflat:.4f} seconds")
print(f"IVFPQ Indexing Time: {indexing_time_ivfpq:.4f} seconds")
print(f"IVFPQ Search Time: {search_time_ivfpq:.4f} seconds")IVFPQ 的索引时间比 IVFFlat 长得多,因为 IVFPQ 在初始聚类后还涉及额外的量化步骤。它应用乘积量化(PQ),需要学习一个码本,将每个向量压缩为多个量化子向量。IVFPQ 的搜索时间略长,这是由于在搜索过程中需要从量化表示中解压缩和重构向量,但差异很小,其内存效率的提升通常值得这额外的搜索时间。
局部敏感哈希(Locality Sensitive Hashing,LSH)
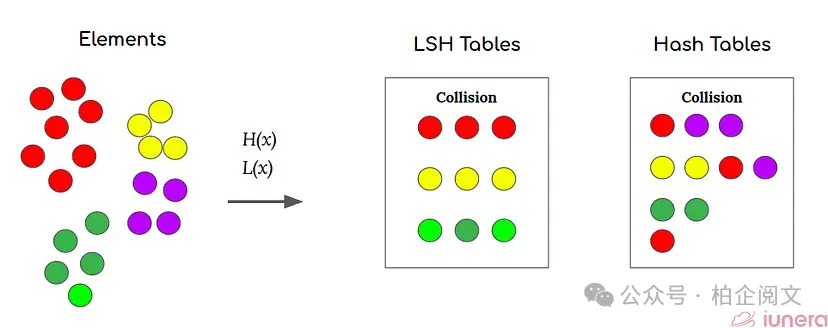
- 工作原理:LSH 将高维向量转换为低维“哈希”值。相似向量更有可能具有相同的哈希值,通过关注包含相关哈希的桶来实现高效搜索。
- 优势:LSH 为相似性搜索提供了一种快速且可扩展的方法,尤其适用于大型数据集和高维空间。
- 关键参数:
哈希表数量:控制准确性和速度之间的权衡。哈希表越多,准确性越高,但搜索时间也会增加。
每个表的哈希函数数量:用于生成每个哈希值的哈希函数数量。
使用 IndexLSH(基于哈希的方法,利用随机投影为每个向量创建哈希值):
nbits = 16
index_lsh = faiss.IndexLSH(d, nbits)
start = time.time()
index_lsh.add(xb)
indexing_time_lsh = time.time() - start
start = time.time()
D, I = index_lsh.search(xq, 5)
search_time_lsh = time.time() - start相似向量更有可能具有相同的哈希值,我们使用 16 位哈希。
输出结果:
print(f"LSH Indexing Time: {indexing_time_lsh:.4f} seconds")
print(f"LSH Search Time: {search_time_lsh:.4f} seconds")LSH 的索引速度极快,因为它只是基于随机投影将数据点哈希到哈希桶中,无需像 IVF 或 HNSW 那样的训练过程,所以索引几乎是即时的。与 IVFFlat 和 HNSW 相比,LSH 的搜索相对较慢,这是因为 LSH 的随机性,可能需要搜索多个哈希桶才能找到最近邻居。LSH 通常索引速度快,但与 HNSW 或 IVFPQ 等更复杂的方法相比,可能会牺牲准确性和搜索速度。
本文只是对大规模相似性搜索领域的简要介绍,仅触及了基础知识,还有更多内容有待探索。未来我们将深入研究实际应用,探索更高级的索引方法,甚至使用 Faiss 构建一些有趣的项目。
本文转载自 柏企阅文,作者: 柏企

















