回复
一文彻底搞懂机器学习 - 聚类与降维（Clustering And Dimensionality Reduction） 原创
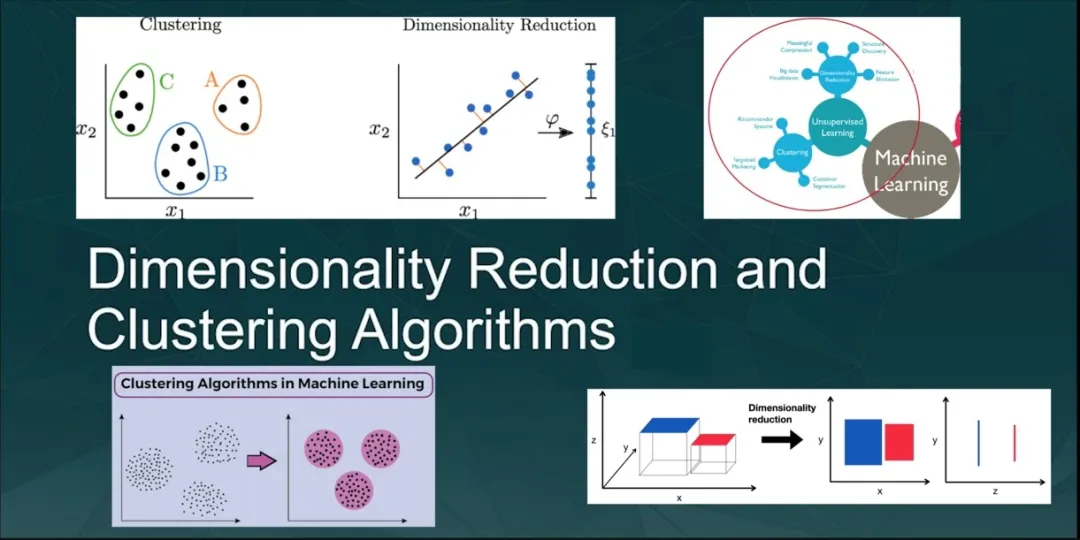
在机器学习中，聚类与降维是两个重要工具，它们能够帮助我们更好地理解和处理高维数据。聚类通过将数据划分为不同的组来揭示数据的内在结构；降维则通过减少数据的维度来简化问题并保留关键信息。
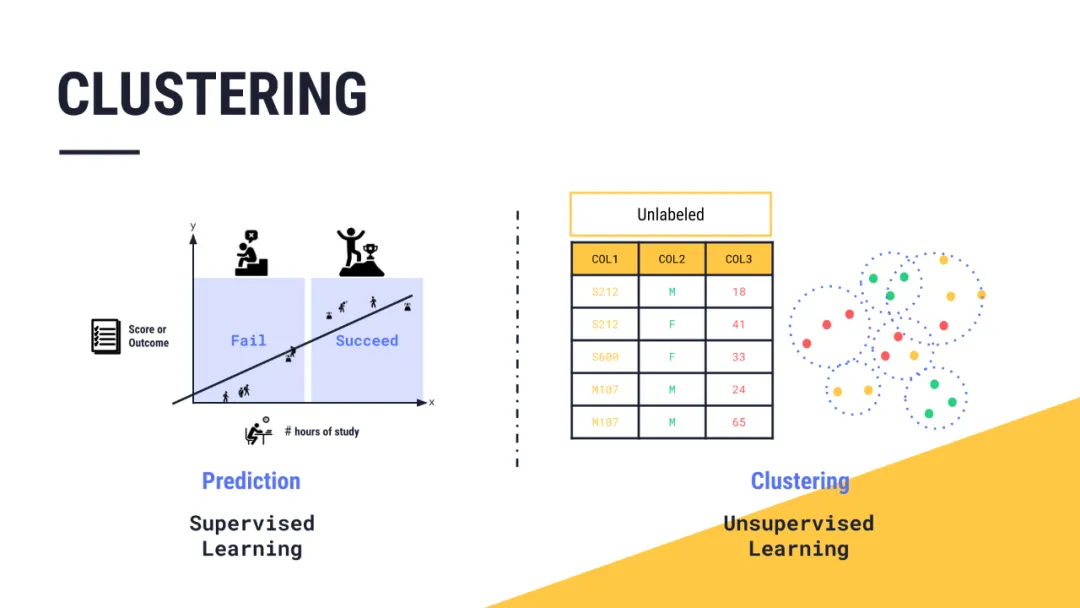
聚类是一种无监督学习算法，通过将数据划分为若干组（簇），使得同一组内的数据点彼此相似，而不同组的数据点差异较大，从而揭示数据的内在结构。
降维是一种数据处理技术，旨在通过某种方法将高维数据转换为低维数据，同时尽量保留数据的原始信息，以便于数据的可视化、特征选择或加速计算等。
Clustering And Dimensionality Reduction
一、聚类
聚类（Clustering）是什么？聚类是一种无监督学习的方法，用于将相似的对象（如数据点、样本、文档、图像等）集合分组成为多个类或簇（Cluster），使得同一簇内的对象尽可能相似，而不同簇之间的对象尽可能不同。
在聚类过程中，不需要事先指定任何标签或类别信息，聚类算法会自动根据数据本身的特征进行分组。
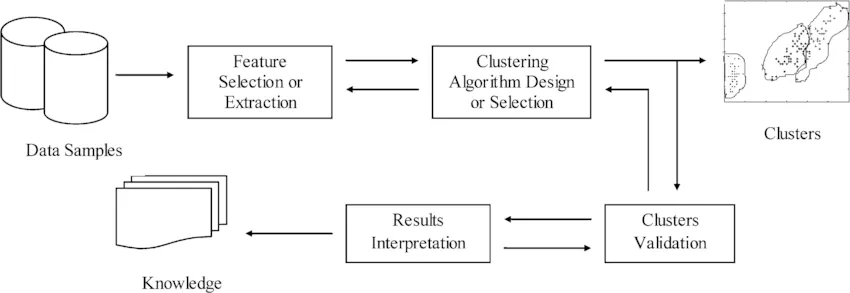
聚类处理流程是什么？数据预处理、选择合适的距离度量、选择聚类算法、初始化聚类中心、迭代更新聚类中心、判断聚类结果、输出聚类结果
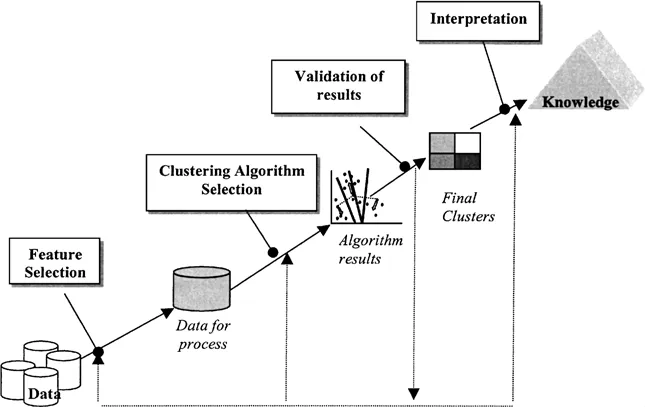
- 数据预处理：确保数据质量，通过清洗、转换、选择和划分，为聚类分析奠定坚实基础。
- 选择合适的距离度量：根据数据特性，选用合适的距离度量方法衡量样本间相似性。
- 选择聚类算法：依据数据特点和需求，挑选适合的聚类算法以揭示数据内在结构。
- 初始化聚类中心：为特定聚类算法（如K-means）设定并随机初始化聚类中心。
- 迭代更新聚类中心：通过重新分配数据点和计算新聚类中心，不断优化聚类结果。
- 判断聚类结果：根据停止条件，评估聚类结果是否满足预设要求。
- 输出聚类结果：将样本分配到不同聚类簇，并通过可视化展示聚类结果。
聚类的算法有哪些？K均值（K-means）、层次聚类（Hierarchical Clustering）、DBSCAN、谱聚类（Spectral Clustering）
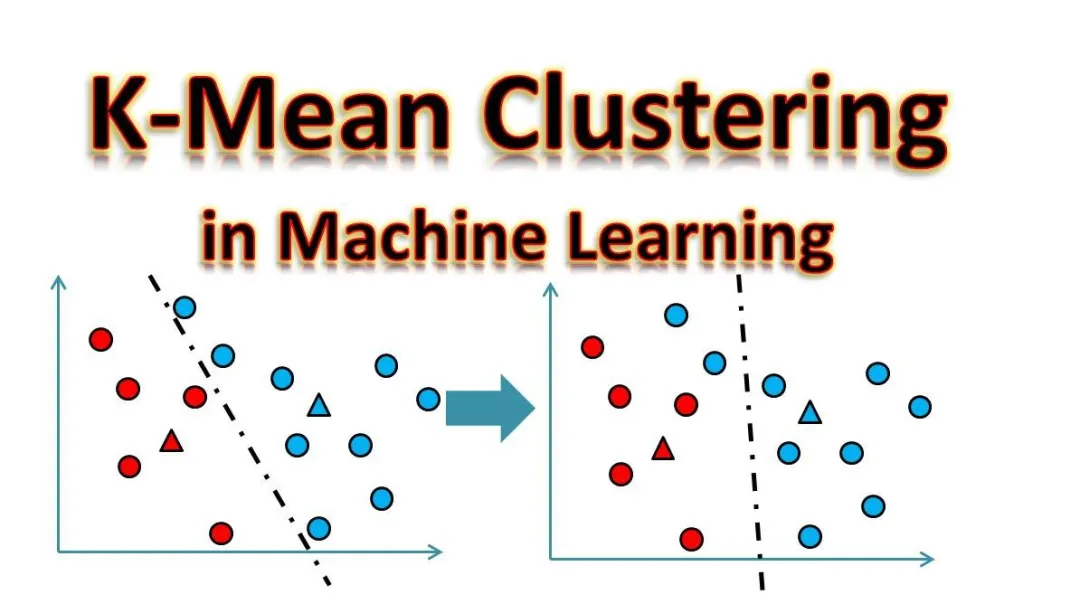
K均值（K-means）：通过迭代将样本划分为K个簇，并更新每个簇的质心，直到满足收敛条件。
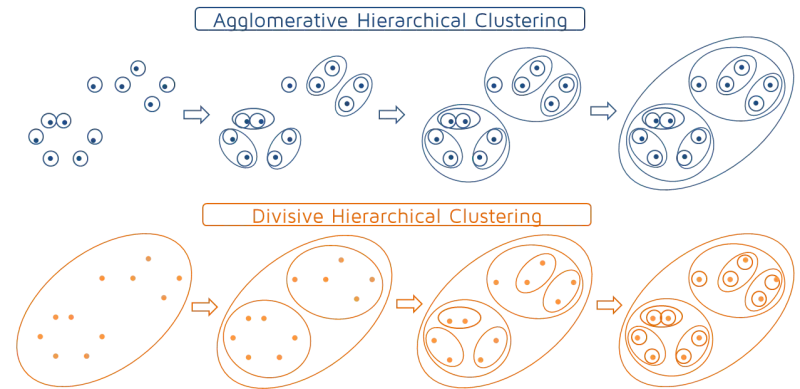
层次聚类（Hierarchical Clustering）：创建一个层次化的聚类树，可以是自底向上的凝聚方法，也可以是自顶向下的分裂方法。
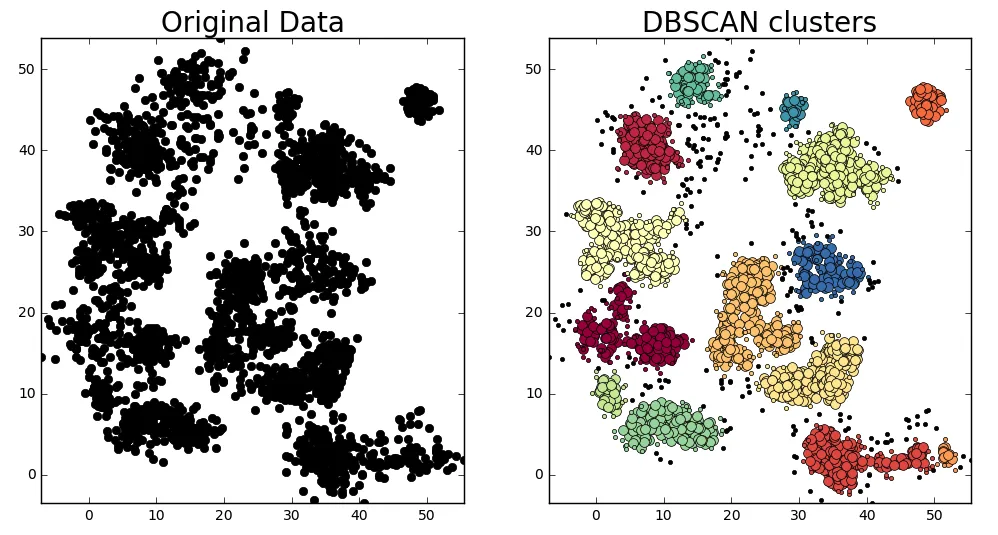
DBSCAN：基于密度的聚类算法，能够识别任意形状的簇，并处理噪声数据。
谱聚类（Spectral Clustering）：将聚类问题转化为图的最优划分问题，通过求解图的拉普拉斯矩阵的特征向量来进行聚类。
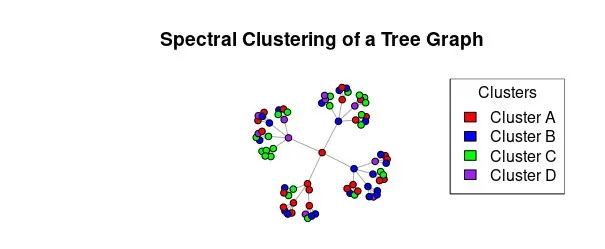
二、降维
降维（Dimensionality Reduction）是什么？降维在机器学习和统计学领域中，是指通过某种数学变换，将原始的高维属性空间转变为一个低维子空间的过程。
降维旨在减少数据集中的特征（变量）数量，同时尽量保留数据的主要信息和结构。
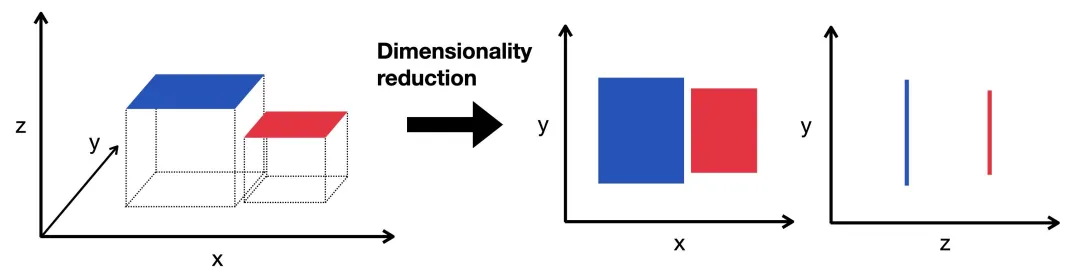
降维处理流程是什么？数据预处理、选择降维方法、实施降维、结果评估和结果输出与应用
- 数据预处理：标准化/归一化是调整数据尺度，确保各特征在相同量级上比较。
- 选择降维方法：根据数据特性，挑选合适的PCA、SVD、t-SNE或LLE等降维技术。
- 实施降维：以PCA为例，通过计算协方差矩阵、特征值分解、选择主成分和数据转换，实现数据降维。
- 结果评估：利用重建误差和方差保留率等方法，确保降维后数据的信息完整性。
- 结果输出与应用：输出降维数据，用于后续分析、可视化或机器学习模型的构建。
降维的算法有哪些？线性降维方法（PCA、ICA、FA、SVD、LDA）、非线性降维方法（UMAP、Iso-map、Kernel PCA）
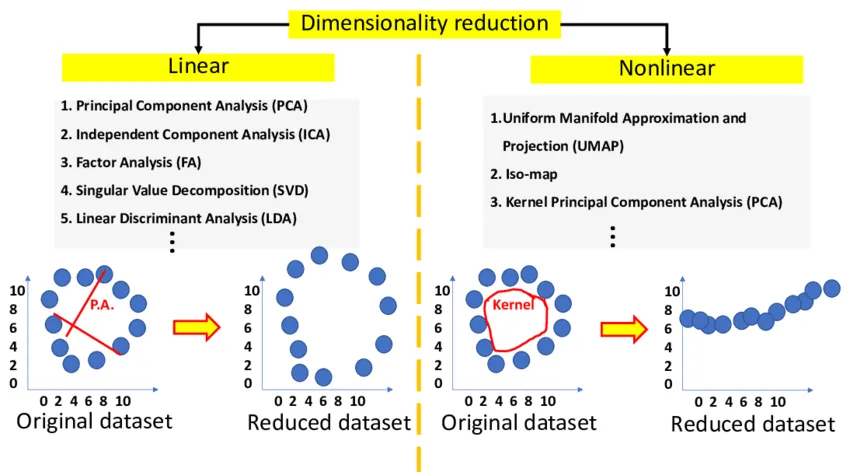
线性降维方法是什么？数据通过线性变换从高维空间映射到低维空间。
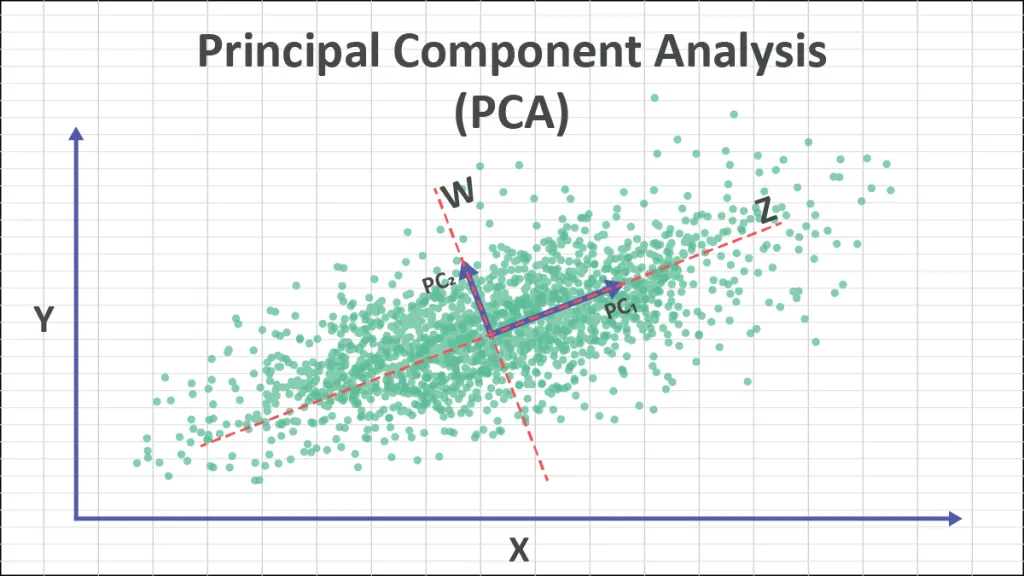
（1）主成分分析（Principal Component Analysis，PCA）
主成分分析（PCA）是一种通过正交变换将可能线性相关的原始变量转换为线性不相关的新变量的方法。这些新变量称为主成分，它们在保留原始数据大部分信息（通常80%以上）的同时，实现了数据的降维。
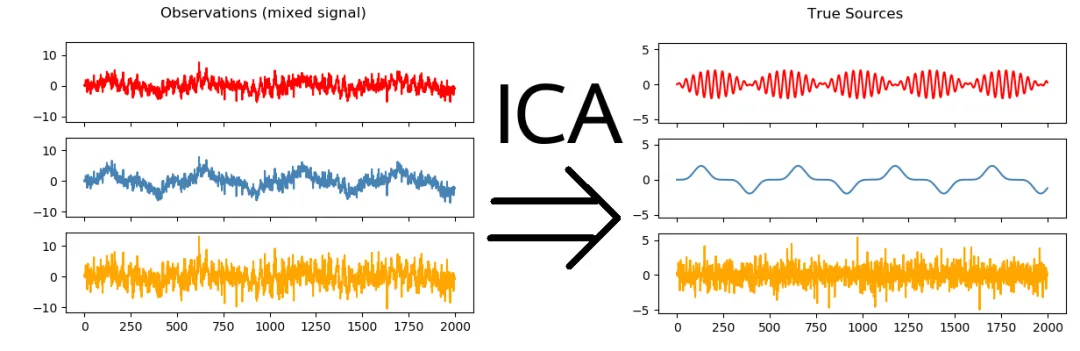
（2）独立成分分析（Independent Component Analysis，ICA）
独立成分分析（ICA）是一种用于多维信号分离的统计方法，旨在将多个混合信号分解为独立的成分。ICA假设原始信号是相互独立的，而不仅仅是相关性低的。
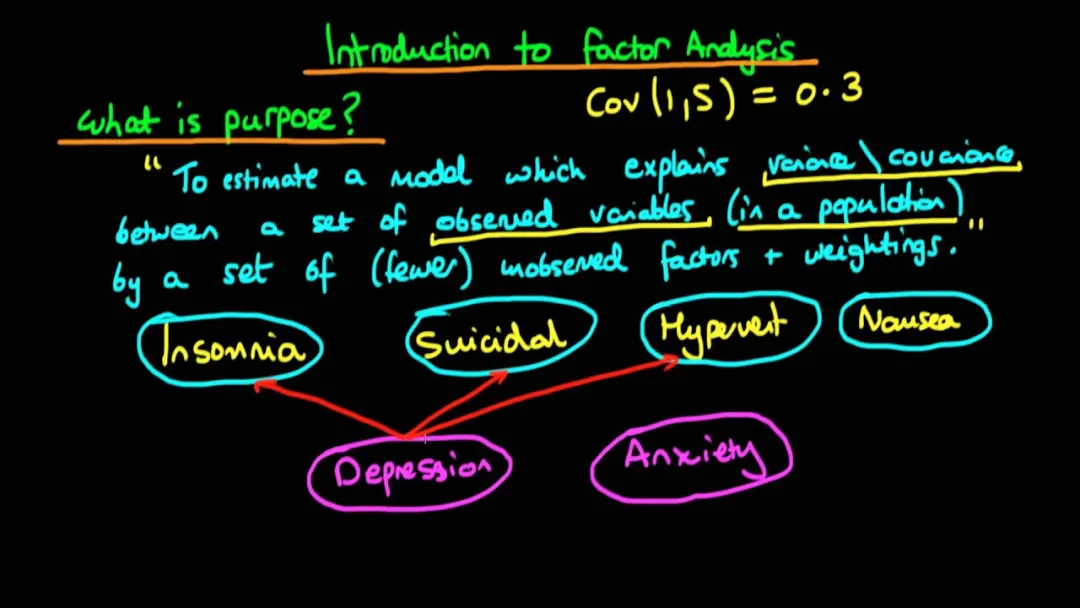
（3）因子分析（Factor Analysis, FA）
因子分析是一种统计方法，旨在探索观察到的变量之间的关系，通过假设这些变量是由少数几个不可观测的潜在因子（或称为“隐变量”）和特定噪声的影响共同生成的。
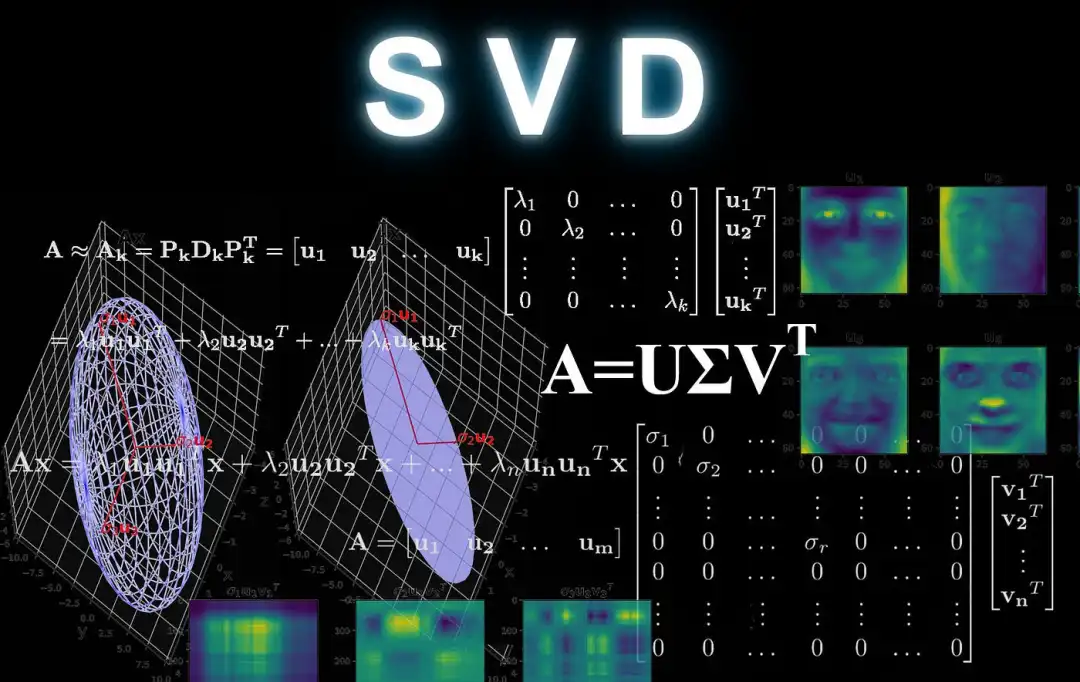
（4）奇异值分解（Singular Value Decomposition, SVD）
SVD是一种矩阵分解方法，可以将一个矩阵分解为三个子矩阵的乘积，常用于数据压缩、降维和信号处理等领域。
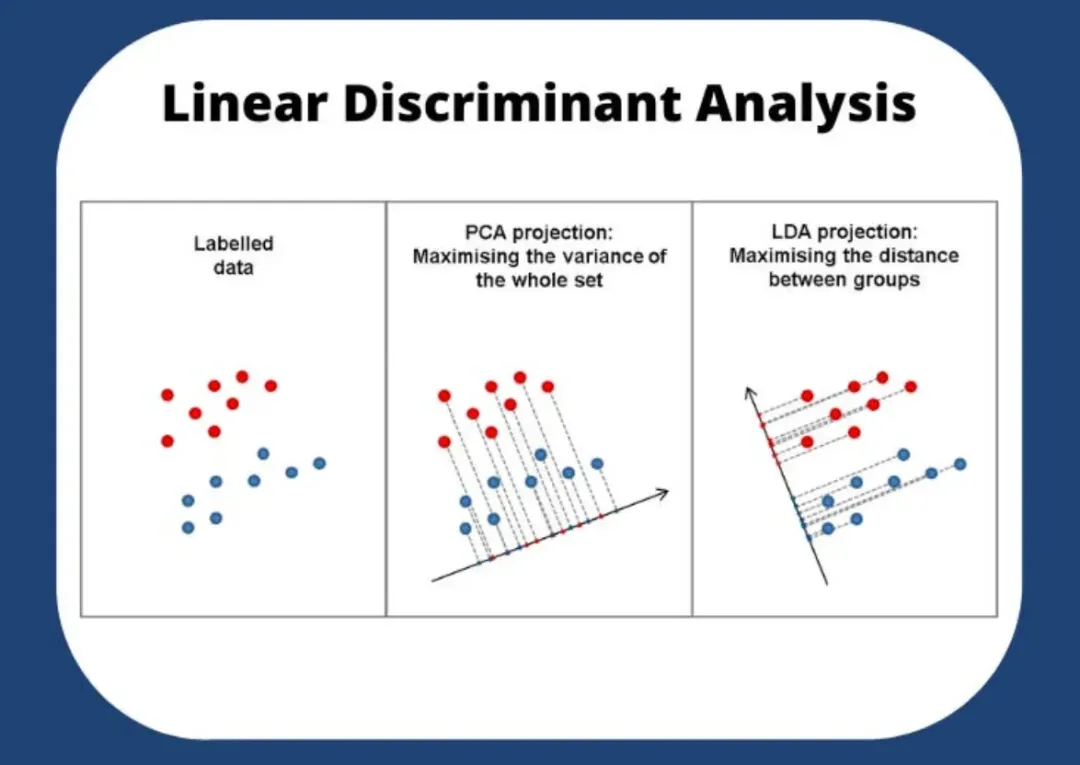
（5）线性判别分析（Linear Discriminant Analysis，LDA）
线性判别分析（LDA）是一种用于分类和降维的线性方法。它通过计算类内散列矩阵和类间散列矩阵，找到能够最大化类间差异和最小化类内差异的线性组合，即投影方向，从而实现数据的降维和分类。
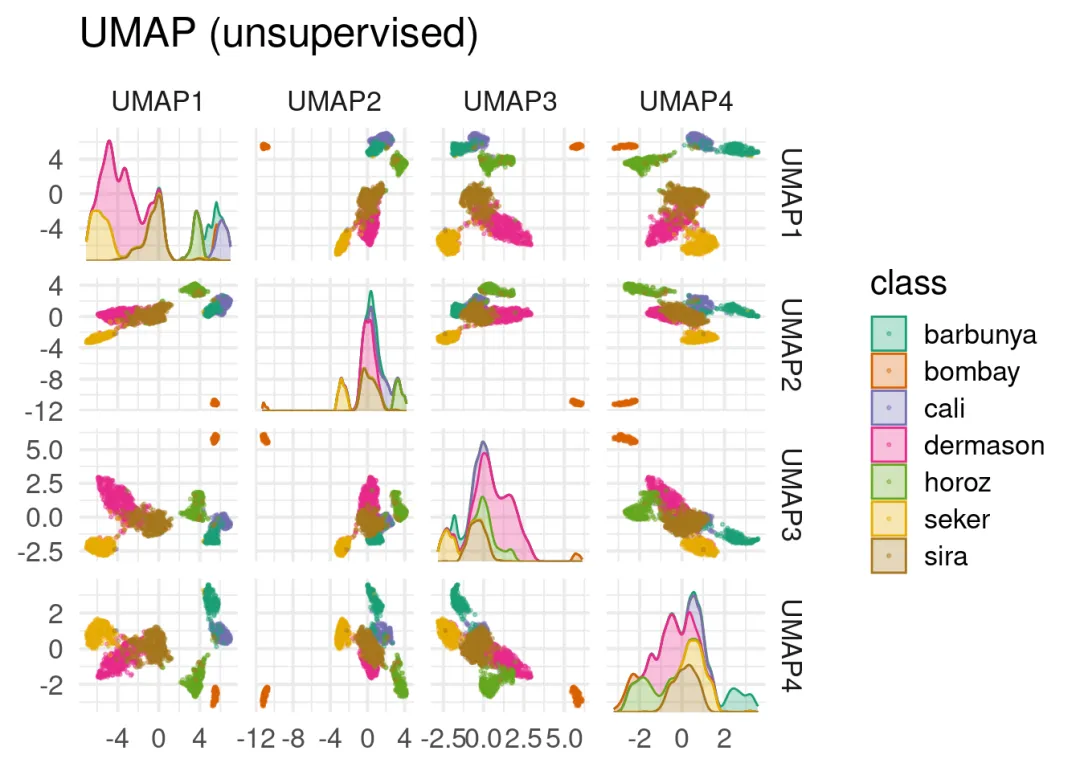
非线性降维方法是什么？与线性降维方法相比，非线性降维方法更能有效地处理非线性结构的数据。
（1）统一流形逼近和投影（Uniform Manifold Approximation and Projection，UMAP）
UMAP（统一流形逼近和投影）是一种降维技术，它利用流形学习技术和拓扑数据分析思想，为处理流形学习和降维提供了一个非常通用的框架。UMAP可用于类似于t-SNE的可视化，但也可用于一般的非线性降维。
（2）等距映射（Isometric Mapping，Iso-map）
Iso-map（等距映射）是一种基于流形学习的非线性降维方法，它试图保留数据内在的由测地线距离蕴含的几何结构。
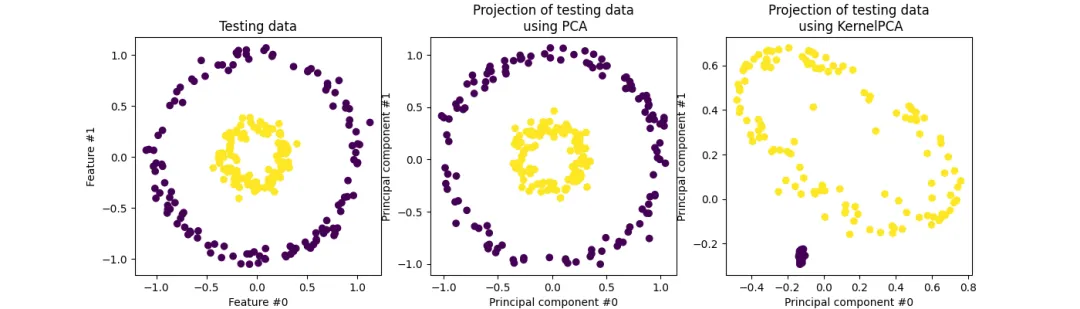
（3）核主成分分析（Kernel Principal Component Analysis，Kernel PCA）
Kernel PCA（核主成分分析）是一种非线性降维方法，它利用核技巧将线性不可分的输入空间映射到线性可分的高维特征空间中，然后在这个高维空间中进行主成分分析（PCA）。
本文转载自公众号架构师带你玩转AI 作者：AllenTang
©著作权归作者所有，如需转载，请注明出处，否则将追究法律责任
标签
已于2024-12-26 16:09:36修改
赞
收藏
回复
相关推荐
