再谈大模型向量，由向量检索引起的思考 原创

“ 向量是大模型技术的基础数据格式，也是用来描述语义关系的核心数学模型 ”

大模型是基于向量作为基础数据格式，这是一个客观存在的事实；但在此之前一直没有深入思考过向量这个问题；最近几天在搞向量数据库的时候，才突然发现向量远远没有想的那么简单。

思考一个简单的问题，向量数据库实现的原理是什么？ 

由向量数据库引起的思考

在上面的问题中，向量数据库的实现原理，说到这个可能很多人会觉得这个问题太复杂；那么就换一种简单的问法，向量检索的原理是什么？

学过中学数学的应该都知道，向量是一种具有大小和方向的量；直观体现就是在平面坐标系中的一个黑色箭头。

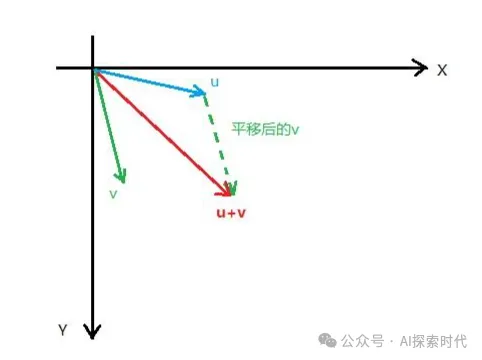
但那时所学的向量属于基础的数学概念，和今天所讲的大模型使用的向量还不是一回事；一般说到向量，我们指的都是空间向量，也就是能在坐标系中画出来，能让我们直观看到的类似空间几何的东西。

但大模型所使用的向量是一种数学概念上的向量，而不是我们所认为的空间向量；比如说320维的向量，谁知道320维是什么样的，四维空间到现在我们还无法想象呢。

大模型所使用的向量，在数学上是通过矩阵来表示的一种数学结构；在编程技术中就是数据结构中的多维数组，或者叫矩阵。

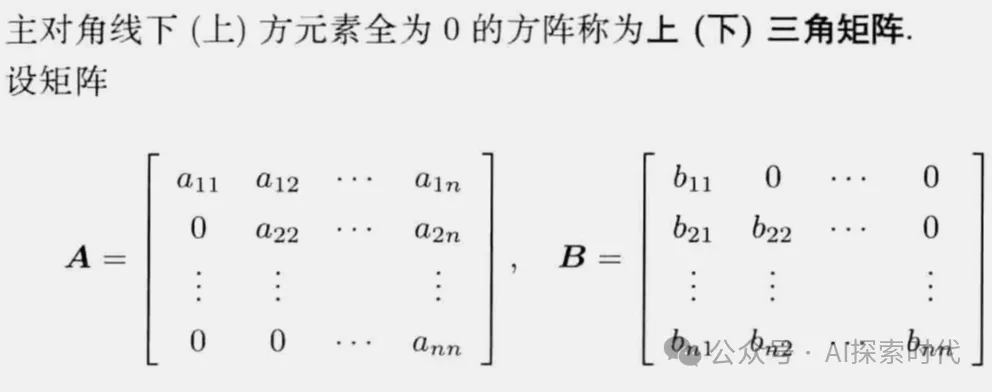
在前面的文章中有说过，之前的检索都是通过字符匹配的方式来实现；但大模型作为人工智能技术的实现方式之一，需要做的不仅仅只是字符匹配，还需要有语义关联。

比如说，我好饿，我想吃饭；这是一句有实际语义的一句话；而如果是一篇文章，一本书，那都是具有实际语义的话；而且同样的话，在不同的语境下会有不同的意义；因此，就需要一种方式来表达或者说描述语义之间的关系，而最终选择的就是向量。

那向量在大模型中的意义是什么？以及其是怎么实现的？

向量是描述大模型系统的一个数学结构，由于大模型的复杂度，因为就需要有一种数学结构去描述这种复杂关系；而向量由于其具有高维性质，因为就刚好可以用来描述复杂的模型关系。比如常见的欧式距离以及余弦相似度，经常被用来计算向量之间的关系，也就是文本(包括其它模态的数据)的语义关系。

而在大模型的发展与具体应用中，大模型所支持的数据格式也越来越多；比如说随着多模态大模型的兴起，大模型所面临的场景越来越复杂，难度也同样呈几何度上升。

而怎么对这种多模态数据进行统一处理，同样需要一种基础的数学结构；而向量刚好能满足这个要求；原因就在于，高维向量的复杂性导致其能涵盖各种复杂的任务场景，并且能够通过数值计算的方式来处理这些数据。

如果从向量的角度来理解大模型训练和微调，那么大模型的训练和微调是在做什么？ 

大模型的训练和微调就是通过一种数据模型，把输入到模型中的训练数据，使用向量去描述其关系，然后根据损失函数的误差，不断的去调整其向量关系的值；最后使得这个值达到最优解；然后把模型的计算参数(大模型的参数)保存下来。

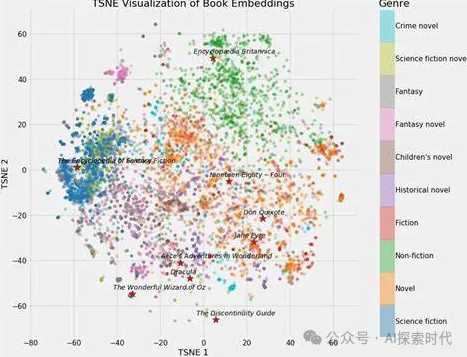
所以，在大模型训练完成之后，就可以通过保存下来的参数来描述新的输入数据；然后根据新数据的要求来生成其向量关系最近的新内容。

从这一点来看，所谓的大模型技术就是寻找一种通用的数学模型；去计算不同模态数据的数学关系；而描述这种数学关系的数学类型就是向量。

所以，如果从这一点进行反推，在未来有一种数学模型能够完全模拟人脑的运作方式；那么就可以用一种数据格式(如向量)来描述大脑的思维过程，实现最终的人工智能。

原文链接：​​https://mp.weixin.qq.com/s/gdQtsJN13gQ-caJlTUFzRg​​