什么是神经网络—终于把梯度下降搞明白了！

 什么是梯度下降？

 梯度下降是一种用于优化目标函数的迭代算法。

什么是目标函数？

就是损失函数，损失函数（Loss Function）是在机器学习和深度学习中广泛使用的一个概念。它主要用于衡量模型的预测结果与实际结果之间的差异程度。简单来说，损失函数的值越小，说明模型的预测越准确。

例如，在一个回归问题（比如预测房价）中，常用的损失函数是均方误差（MSE）。假设真实房价是y ，模型预测的房价是y^，均方误差损失函数可以表示为：

这里n是样本数量。该函数通过计算每个样本预测值和真实值差的平方的平均值，来衡量整体的误差。我们的目标就是使得误差降到最低，使预测值无限接近真实值，所以我们使用梯度下降来做到这一步。

梯度下降如何优化损失函数？

举个例子来说明这一步，假设我们需要拟合一条直线，这条直线的横坐标是体重，纵坐标是身高，如下所示（绿色的点是数据点，绿色的线是我们要拟合的线）：

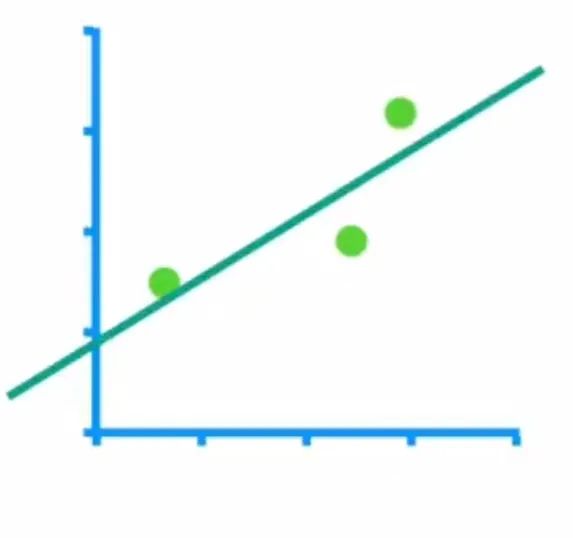
这条直线的方程是y=w*x+b，三个数据坐标点的分别是(0.5,0.8),(2.5,2),(3,3)。我们先求出损失函数，这个损失函数才是我们要优化的参数。我们使用MSE作为损失函数。

得到损失函数Loss=((0.8-w*0.5-b)平方+(2-w*2.5-b)平方+(3-w*3-b)平方)/3。

我们可以看到损失函数Loss就是关于w和b两个参数的函数。我们将Loss函数的图像画出来如下图所示：

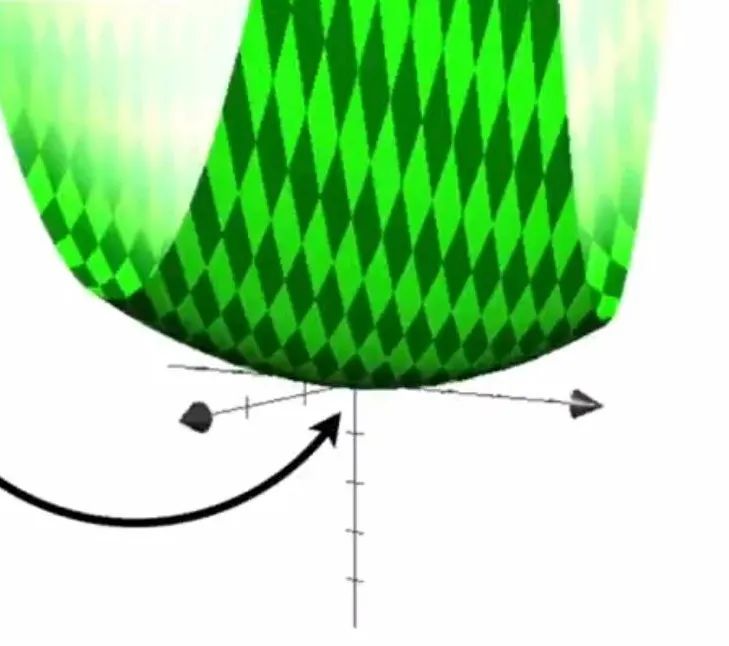
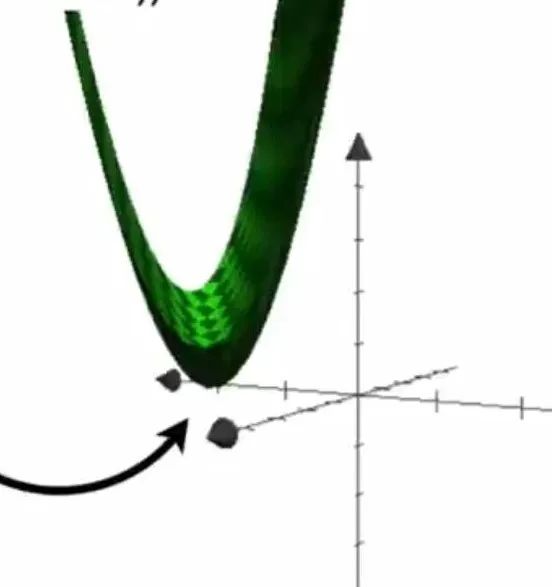
上面的图片中x轴是w，y轴是b，z轴是Loss。我们要找的就是Loss处于最低点处的w和b的值。

那我们怎么找呢？

就要使用梯度下降。梯度就是导数，就是参数在某一点的变化率，在曲线上可以反映为某一点的切线。对于多元函数来说，梯度就是一个向量，它包含了函数对各个向量的偏导数，这个梯度的向量指向函数值增长最快的方向。我们知道导数为0时，函数处于极值点。所以我们沿着梯度下降就可以最快的到达损失函数极小值点。

 梯度下降的做法就是损失函数分别对参数求导，比如说当w为固定值时，损失函数Loss对b的函数图像如下所示，图片中的斜率时Loss对b的导数，也就是b的梯度：

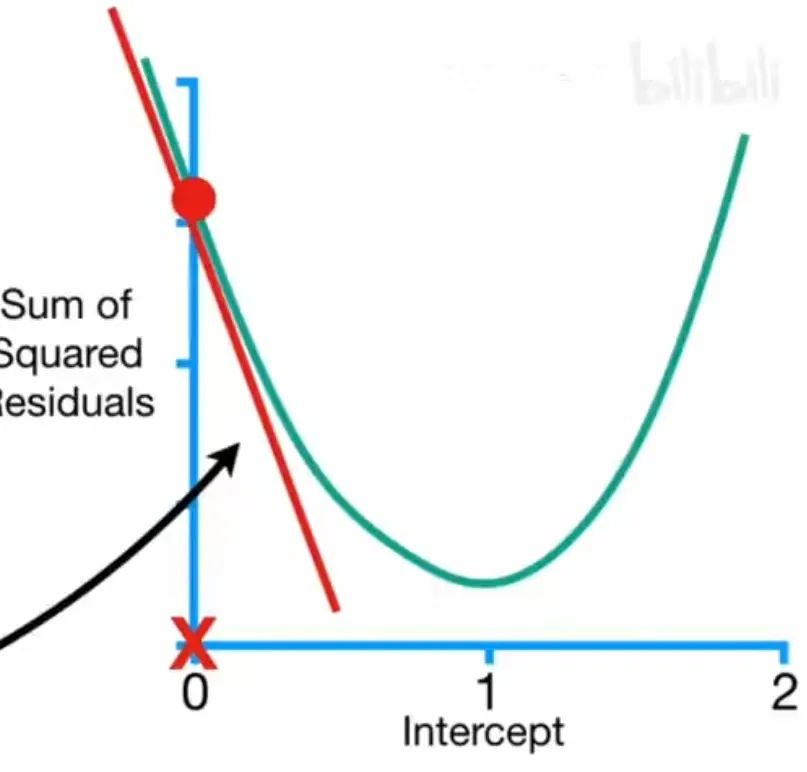
当b=0时，Loss很大，梯度(斜率)很大。

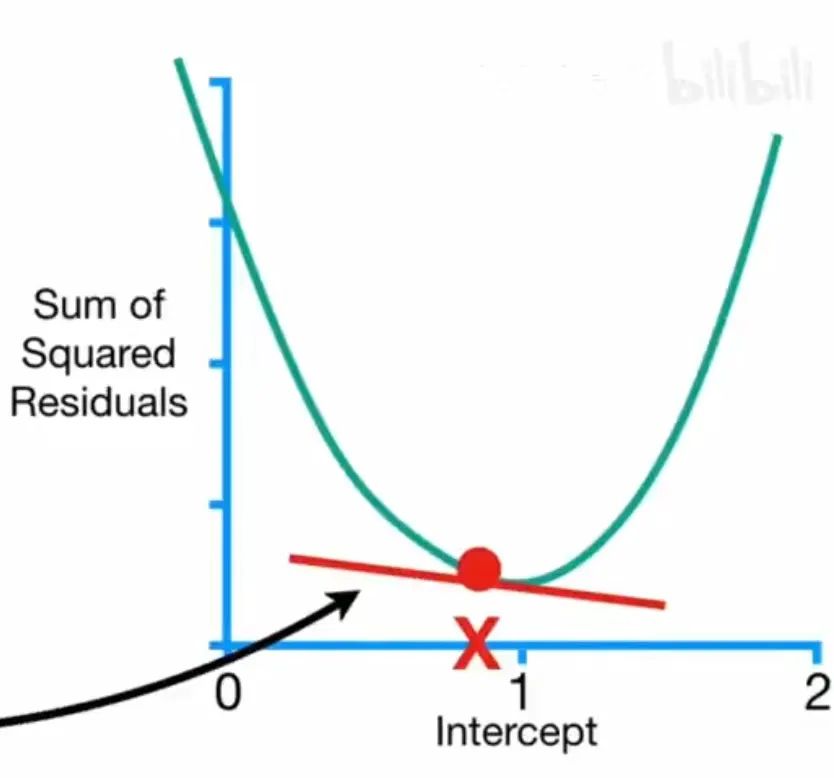
当b=0.8时，Loss趋近最小值，梯度(斜率)很小。

由此我们可以看到，当斜率也就是梯度很大的时候，b可以增大一点步长，以便于快速到达极值点；当斜率也就是梯度很小的时候说明很快逼近最小值，b可以减小一点步长；所以b可以这样更新：

                    b=b-（Loss对b的梯度）*学习率

梯度大的时候b就可以迈大一步，梯度小的时候b就可以迈小一步，这里学习率一般设置比较小，避免迈的步子太大直接跳过极小值点。

所以梯度下降的步骤一般如下所示：

1. 对损失函数中每个参数求导，也就是求梯度

2. 对参数随机赋值

3. 将参数值带入梯度

4. 计算步长

5. 更新参数

6. 回到步骤3重新计算，直到步长（（Loss对b的梯度）*学习率）小于设置阈值。

怎么样？看上去很晦涩的东西是不是也没那么难懂？是不是对梯度下降非常了解了？！

本文转载自 ​​人工智能训练营​​，作者： 小A学习