中山大学、美团联合团队推出行为正则化与顺序策略优化结合的离线多智能体学习算法

离线多智能体强化学习（MARL）是一个新兴领域，目标是在从预先收集的数据集中学习最佳的多智能体策略。相比于单智能体情况，多智能体环境涉及到大规模的联合状态-动作空间和多智能体间的耦合行为，这给离线策略优化带来了额外的复杂性。随着人工智能技术的发展，多智能体系统在诸如自动驾驶、智能家居和机器人协作等方面展现了巨大的应用潜力。但是离线MARL较单智能体情况下更加复杂，其涉及庞大的联合状态-动作空间和多智能体间的复杂互动行为，这使得离线策略优化成为一项艰巨的任务。

离线MARL面临的主要挑战包括：一是如何有效应对分布偏移问题，即在策略评估过程中，分布外（OOD）样本可能导致误差积累；二是在多智能体环境下，协调多个智能体的行为显得尤为困难。现有的离线MARL方法尽管取得了一些进展，但仍存在不协调行为和分布外联合动作的问题。为了应对这些挑战，来自中山大学、美团的联合团队提出了一种新颖的离线MARL算法——样本内顺序策略优化（In-Sample Sequential Policy Optimization, InSPO），该方法通过顺序更新每个智能体的策略，避免选择OOD联合动作，同时增强了智能体之间的协调。

12月 11 日，arXiv发表了他们的技术论文《Offline Multi-Agent Reinforcement Learning via In-Sample Sequential Policy Optimization》。研究团队的主要贡献在于提出了InSPO算法，该算法不仅避免了OOD联合动作，还通过探索行为策略中的低概率动作，解决了提前收敛到次优解的问题。理论上InSPO保证了策略的单调改进，并收敛到量化响应均衡（QRE）。实验结果表明，InSPO在多个离线MARL任务中表现出了显著的效果，与当前最先进的方法相比具有明显的优势。

研究团队成员又来自中山大学计算机科学与工程学院的Zongkai Liu, Qian Lin, Chao Yu和Xiawei Wu、上海创新研究院的Zongkai Liu和美团的Yile Liang, Donghui Li和Xuetao Ding，涵盖了学术界和工业界的专家，致力于多智能体强化学习和行为优化等领域的研究。

合作型马尔可夫游戏

在理解离线多智能体强化学习（MARL）中的样本内顺序策略优化之前，首先需要了解合作型马尔可夫游戏的基本概念和框架。

图1:XOR游戏。（a） 是联合行动的奖励矩阵。（b） 是数据集的分布。

定义与基本概念

合作型马尔可夫游戏是一种多智能体系统的建模方法，它能够有效地描述多个智能体在同一环境中进行交互的过程。这个游戏模型定义为G=⟨N,S,A,P,r,γ,d⟩G = \langle N, S, A, P, r, \gamma, d \rangle。其中，NN是智能体的集合，SS是有限的状态空间，AA是联合动作空间，包含了所有智能体的动作集合。转移概率函数PP描述了从一个状态到另一个状态的转移可能性，公共奖励函数rr则为所有智能体提供统一的奖励反馈。折扣因子γ\gamma和初始状态分布dd分别影响未来奖励的权重和初始状态的选择。在每一个时间步tt，每个智能体ii在状态sts_t选择动作aita_i^t，并依次移动到下一个状态st+1s_{t+1}，同时根据联合动作接收奖励。

IGM原则与值分解

在多智能体系统中，直接计算联合Q函数是一个极其复杂的问题，因为状态-动作空间会随着智能体数量的增加而指数级增长。值分解方法通过将联合Q函数分解为每个智能体的个体Q函数，极大地简化了这个计算过程。具体来说，联合Q函数Q(s,a)Q(s, a)被表示为每个智能体Q函数QiQ_i的组合。这种分解方式依赖于个体-全局-最大化（IGM）原则，即最优联合动作可以通过每个智能体的贪婪动作来识别。然而，这种方法在处理环境中存在多模态奖励景观时可能会遇到困难，因为IGM假设往往会被破坏。

图2:M-NE游戏。（a） 是联合行动的奖励矩阵。（b） 是数据集的分布。

离线MARL中的行为正则化马尔可夫游戏

为了有效应对离线MARL中的分布偏移问题，行为正则化马尔可夫游戏引入了一个与数据相关的正则化项。这个正则化项通过在奖励函数中加入额外的惩罚，迫使学习到的策略尽量接近行为策略，从而避免选择分布外的动作。在这个框架中，策略的目标是最大化期望折扣回报，同时减去正则化项，以此平衡策略的探索和利用。这样不仅提高了策略的稳定性，还能防止其收敛到局部最优解。

通过引入这些基础概念和原理，合作型马尔可夫游戏为多智能体系统的行为建模和优化提供了一个强大的工具。尤其在离线环境中，结合行为正则化和值分解方法，可以有效解决多智能体间的协调问题，并提高策略的整体表现。

样本内顺序策略优化

在离线多智能体强化学习（MARL）中，策略的优化往往面临着分布外（OOD）联合动作和局部最优解问题。为了应对这些挑战，研究团队提出了一种创新的方法——样本内顺序策略优化（In-Sample Sequential Policy Optimization, InSPO）。该方法在行为正则化马尔可夫游戏框架下进行，结合了逆KL散度和最大熵正则化，旨在通过顺序更新每个智能体的策略，避免选择OOD联合动作，同时增强智能体之间的协调。

样本内顺序策略优化的数学推导

InSPO方法的核心在于通过逆KL散度进行行为正则化，从而确保学习到的策略与行为策略共享相同的支持集，避免选择分布外的动作。具体来说，目标函数中的逆KL散度项可以分解为各个智能体的独立项，这使得顺序更新每个智能体的策略成为可能。数学上通过使用Karush-Kuhn-Tucker（KKT）条件，推导出目标函数的闭式解，从而实现样本内学习。最终的优化目标为最小化KL散度，以确保策略更新的有效性和一致性。

最大熵行为正则化马尔可夫游戏

为了进一步增强探索性，防止策略过早收敛到局部最优解，InSPO引入了最大熵行为正则化马尔可夫游戏（MEBR-MG）框架。在这个框架中，策略优化的目标函数不仅包含逆KL散度项，还引入了策略熵项。通过这种方式，优化目标能够促使策略在高概率动作和低概率动作之间保持平衡，鼓励充分探索低概率动作，从而避免局部最优解。理论上，最大熵行为正则化还能够确保策略收敛到量化响应均衡（QRE），即在面对扰动奖励时，策略仍能维持稳定的性能。

通过上述方法，样本内顺序策略优化不仅有效解决了离线MARL中的OOD联合动作问题，还通过策略熵的引入，显著提高了策略的探索能力和全局最优解的发现概率。

算法细节

算法 1: InSPO 的步骤

InSPO算法的核心在于通过顺序更新的方式，逐步优化每个智能体的策略，最终实现全局最优。具体步骤如下：

1. 输入：离线数据集DD、初始策略π0\pi_0和初始Q函数Q0Q_0。
2. 输出：最终策略πK\pi_K。
3. 首先，通过简单的行为克隆方法计算出行为策略μ\mu。
4. 接下来，开始迭代优化。在每一轮迭代中，先计算出当前Q函数QkQ_k。
5. 随机抽取一个智能体的排列i1:Ni_{1:N}，并依次更新每个智能体的策略。
6. 对于每个智能体，使用推导出的目标函数进行策略更新。
7. 重复上述过程，直到达到预定的迭代次数KK。

这种顺序更新的策略，确保了每一步的策略优化都是在样本内进行的，避免了分布外动作的选择，提高了策略的稳定性和有效性。

策略评估

策略评估是InSPO算法中的一个关键步骤。根据更新的Q函数，计算当前策略的期望回报。在多智能体环境中，由于联合动作空间的庞大，研究团队采用了局部Q函数来进行近似。在策略评估过程中，需要顺序地更新每个智能体的局部Q函数，使其能反映最新的策略信息。具体的目标函数包括一个权重项，用于平衡策略的探索和利用。此外，为了降低重要性采样比率的高方差，InSPO采用了重要性重采样技术，通过概率比例重采样构建新的数据集，从而稳定算法的训练效果。

策略改进

在获得优化的局部Q函数后，接下来就是策略改进步骤。通过最小化KL散度，InSPO能够在保持行为策略特性的同时，逐步优化每个智能体的策略。在具体操作中，使用推导出的目标函数来指导每个智能体的策略更新，这一过程确保了策略的收敛性和改进性。

实际应用及实现细节

在实际应用中，InSPO不仅需要在理论上保证策略的有效性，还需要在大规模状态-动作空间中保持高效的计算性能。为了实现这一点，我们对算法进行了多方面的优化：

局部Q函数的优化：为了避免联合动作空间的指数级增长，我们使用局部Q函数来近似全局Q函数，并通过顺序更新的方法逐步优化每个智能体的局部Q函数。

重要性重采样：通过重要性重采样技术，构建新的数据集，降低采样比率的方差，提高训练的稳定性。

自动调节温度参数α：为了找到合适的保守程度，我们实现了自动调节α的机制，根据目标值进行动态调整，从而进一步提高性能。

这些优化措施使得InSPO在处理复杂的多智能体任务时，能够保持高效的性能和良好的收敛性。通过这些实际应用和实现细节，InSPO展现了其在离线MARL中的巨大潜力和应用价值。

实验验证

在M-NE游戏中，研究团队评估了InSPO对局部最优收敛问题的缓解能力。实验使用两个数据集：一个是由均匀策略收集的平衡数据集，另一个是由接近局部最优的策略收集的不平衡数据集。结果显示，在平衡数据集上，大多数算法都能找到全局最优解，而在不平衡数据集上，只有InSPO正确识别出全局最优解。这表明，在存在多个局部最优解的环境中，数据集分布对算法收敛性有显著影响。InSPO通过全面探索数据集，避免了次优解的影响，展现了其强大的全局最优解识别能力。

桥游戏的实验结果

桥游戏是一个类似于时间版本XOR游戏的网格世界马尔可夫游戏。在这个实验中，我们使用了两个数据集：optimal数据集和mixed数据集。optimal数据集包含了由最优确定性策略生成的500条轨迹，而mixed数据集则包括optimal数据集和由均匀随机策略生成的额外500条轨迹。实验结果表明，只有InSPO和AlberDICE在这两个数据集上都达到了近乎最优的性能。相比之下，值分解方法未能收敛，并产生了不理想的结果。这进一步证明了InSPO在复杂多智能体任务中的有效性。

图3：数据集XOR博弈的最终联合策略（b）。

星际争霸II微操作基准测试的实验结果

为了进一步验证InSPO的性能，研究团队将研究扩展到星际争霸II微操作基准测试，这是一个高维复杂的环境。实验使用了四个代表性地图，并采用了四个不同的数据集：medium、expert、medium-replay和mixed。在这些实验中，尽管值分解方法在该环境中表现出色，InSPO依然展示了其竞争力，在大多数任务中取得了最先进的结果。实验结果证明了InSPO在高维复杂环境中的应用潜力。

表1-4：星际争霸II微管理的平均测试获胜率。

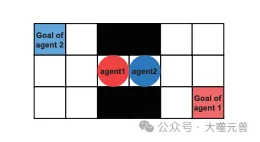
      图4：开始时的桥。

消融研究

为了评估InSPO中不同组件的影响，研究团队进行了消融研究。首先他们在不平衡数据集上的M-NE游戏中测试了去除熵项的InSPO，结果显示没有熵扰动的InSPO无法逃离局部最优。他们在XOR游戏中测试了同时更新而非顺序更新的InSPO，由于更新方向的冲突，未能学习到最优策略，并面临OOD联合动作问题。此外，研究团队还评估了温度参数α对策略保守程度的影响，结果表明自动调节的α能够找到合适的值，进一步提升性能。

图5：熵消融和顺序更新方案。（a） 对于不平衡数据集，在M-NE博弈中没有熵的InSPO。（b） 是数据集（b）XOR游戏上InSPO的同步更新版本。

通过这些实验验证，InSPO展现了其在解决离线MARL中的局部最优收敛问题、增强策略探索能力和提高全局最优解识别能力方面的优势。实验结果不仅证明了InSPO的理论可行性，还展示了其在实际应用中的强大潜力。

结论

在本研究中，研究团队提出了一种新颖的离线多智能体强化学习（MARL）算法——样本内顺序策略优化（In-Sample Sequential Policy Optimization, InSPO）。通过引入逆KL散度和策略熵，他们有效地解决了离线MARL中的分布外（OOD）联合动作和局部最优解问题。理论分析和实验验证表明，InSPO不仅能够实现策略的单调改进，并最终收敛到量化响应均衡（QRE），还在多个基准测试中展示了优越的性能。与现有的离线MARL方法相比，InSPO在应对复杂多智能体任务、提高策略稳定性和探索能力方面具有显著优势。

尽管InSPO在离线MARL领域取得了突破性的进展，但仍有许多值得进一步探索的方向。

算法扩展与优化：未来可以考虑将InSPO与其他先进的MARL算法相结合，进一步提升策略优化的效果。同时，研究如何在更大规模、更复杂的环境中实现高效的策略优化，也是一个重要的方向。

数据集增强与生成：在离线MARL中，数据集的质量和分布对算法性能有着直接影响。未来可以探索通过生成对抗网络（GANs）等技术生成高质量的数据集，从而改善策略学习的效果。

多模态奖励景观的应对：在存在多个局部最优解的环境中，如何更有效地识别和收敛到全局最优解，仍是一个具有挑战性的问题。研究新的正则化方法和优化策略，能够进一步提升InSPO的鲁棒性。

实际应用与验证：将InSPO应用到更多实际场景中，如智能交通系统、自动驾驶和智能制造等，验证其在真实环境中的性能和稳定性，将是未来的重要研究方向。

通过这些方向的深入研究与探索，我们有望进一步提升离线MARL算法的性能和应用价值，推动人工智能技术在多智能体系统中的广泛应用。（END）

参考资料：https://arxiv.org/abs/2412.07639

本文转载自​​大噬元兽​​，作者： FlerkenS ​​​​