一文彻底搞懂机器学习 - 支持向量机(SVM) 原创
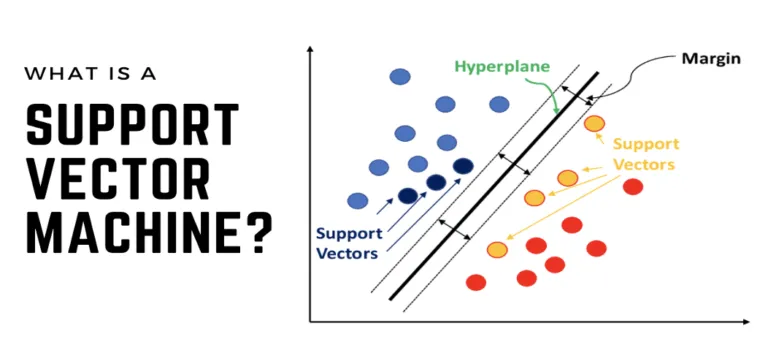
SVM是一种强大的机器学习算法,适用于线性可分和线性不可分的数据分类问题,以及回归任务。通过构建最优超平面和最大化间隔,SVM能够实现高效且准确的分类和回归预测。
线性SVM分类通过构建最优超平面最大化类别间隔实现数据分类;非线性SVM分类利用核函数将数据映射至高维特征空间以找到可分隔超平面进行分类;SVM回归则通过最优化超平面使数据点预测误差在给定范围内,实现回归预测。
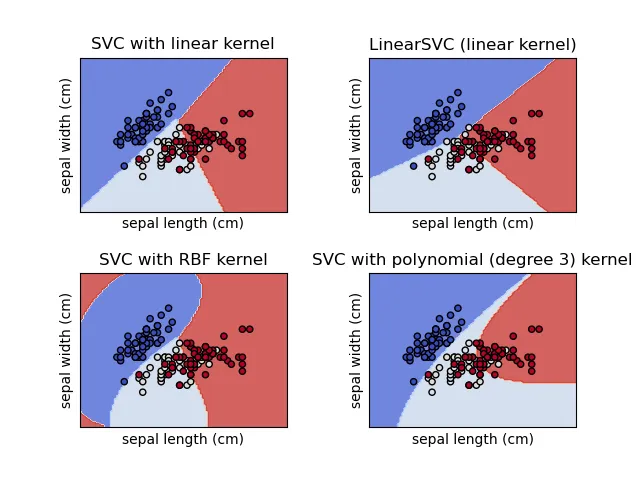
SVM
一、线性SVM分类
线性SVM(Linear Support Vector Machine)是什么?线性SVM是一种用于二分类问题的监督学习算法。
线性SVM分类的核心思想是通过构建一个最优超平面,将不同类别的数据样本分隔开来,并且具有最大的间隔(即离超平面最近的数据点的距离最大化)。

线性SVM如何实现线性分类?线性SVM(支持向量机)通过找到一个线性决策边界来实现线性分类。
这个决策边界是一个超平面(在二维空间中是一条直线,三维空间中是一个平面,以此类推),它将数据集中的样本分成两个类别。线性SVM的目标是找到一个最优的超平面,使得两类样本之间的间隔最大化。
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
# 数据生成
np.random.seed(0)
X = np.random.randn(100, 2) # 100个样本,每个样本2个特征
y = (X[:, 0] + X[:, 1] > 0).astype(int) * 2 - 1 # 生成标签,+1/-1
# 转换为PyTorch张量
X_train = torch.tensor(X, dtype=torch.float32)
y_train = torch.tensor(y, dtype=torch.float32).view(-1, 1) # 保持与PyTorch习惯一致的形状
# 模型定义
class LinearSVM(nn.Module):
def __init__(self):
super(LinearSVM, self).__init__()
self.linear = nn.Linear(2, 1) # 输入特征数为2,输出为1(决策边界的权重)
def forward(self, x):
return self.linear(x)
# 实例化模型、定义损失函数和优化器
model = LinearSVM()
criterion = nn.HingeEmbeddingLoss() # Hinge loss for SVM
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 模型训练
num_epochs = 100
for epoch in range(num_epochs):
model.train()
optimizer.zero_grad()
outputs = model(X_train).squeeze() # 去除输出张量的额外维度
loss = criterion(outputs * y_train, torch.ones_like(y_train)) # 注意:HingeEmbeddingLoss的输入要求
loss.backward()
optimizer.step()
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')
# 获取决策边界
def get_decision_boundary(model, x_range=(-3, 3), y_range=(-3, 3), num_points=100):
x0_vals = torch.linspace(x_range[0], x_range[1], num_points)
x1_vals = torch.linspace(y_range[0], y_range[1], num_points)
grid = torch.meshgrid(x0_vals, x1_vals)
grid_points = torch.stack([grid[0].flatten(), grid[1].flatten()], dim=1)
outputs = model(grid_points).detach().numpy()
decision_boundary = outputs.reshape(num_points, num_points)
return x0_vals, x1_vals, decision_boundary
# 可视化
def plot_data_and_boundary(X, y, model, x_range=(-3, 3), y_range=(-3, 3)):
plt.scatter(X[y == 1, 0], X[y == 1, 1], c='r', label='Class +1')
plt.scatter(X[y == -1, 0], X[y == -1, 1], c='b', label='Class -1')
x0_vals, x1_vals, decision_boundary = get_decision_boundary(model, x_range, y_range)
plt.contour(x0_vals.numpy(), x1_vals.numpy(), decision_boundary, levels=[0], linestyles='--', colors='k')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()
# 绘制数据和决策边界
plot_data_and_boundary(X_train.numpy(), y_train.numpy().flatten(), model)
二、非线性SVM分类
非线性SVM(Non-linear Support Vector Machine)是什么?对于线性不可分的数据,非线性SVM通过核函数将数据映射到高维特征空间,使其在该空间中可线性分隔。
在传统的线性SVM中,我们寻找一个线性决策边界来分隔不同类别的数据点。然而,当数据在原始空间中不是线性可分时,线性SVM的效果就不理想了。
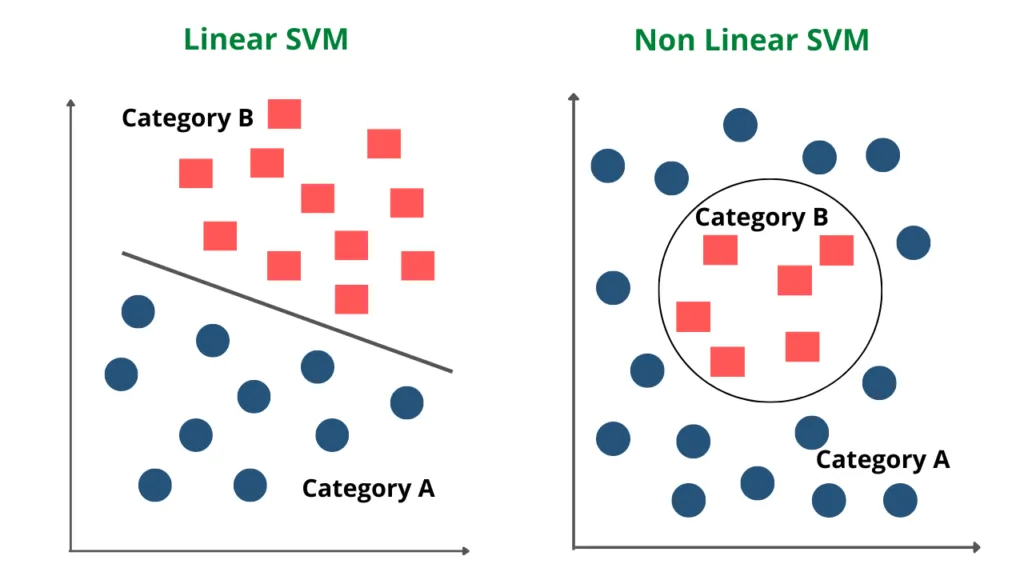
非线性SVM如何实现非线性分类?非线性SVM使用核技巧来解决数据非线性可分的问题。核技巧让我们能在高维特征空间中创建线性决策边界,尽管在原始空间中这个边界看起来是非线性的。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets, svm, metrics
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_moons
# 生成一个非线性可分的数据集
X, y = make_moons(n_samples=100, noise=0.2, random_state=42)
# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 数据标准化(对于SVM来说通常很重要)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 训练非线性SVM模型,使用RBF核
clf = svm.SVC(kernel='rbf', gamma='scale', C=1.0)
clf.fit(X_train, y_train)
# 在测试集上预测
y_pred = clf.predict(X_test)
# 计算准确率
accuracy = metrics.accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")
# 可视化(仅适用于二维数据集)
def plot_decision_boundary(clf, X, y, title=''):
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
np.arange(y_min, y_max, 0.01))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
plt.title(title)
plt.show()
# 绘制训练集的决策边界
plot_decision_boundary(clf, X_train, y_train, title='Training set decision boundary')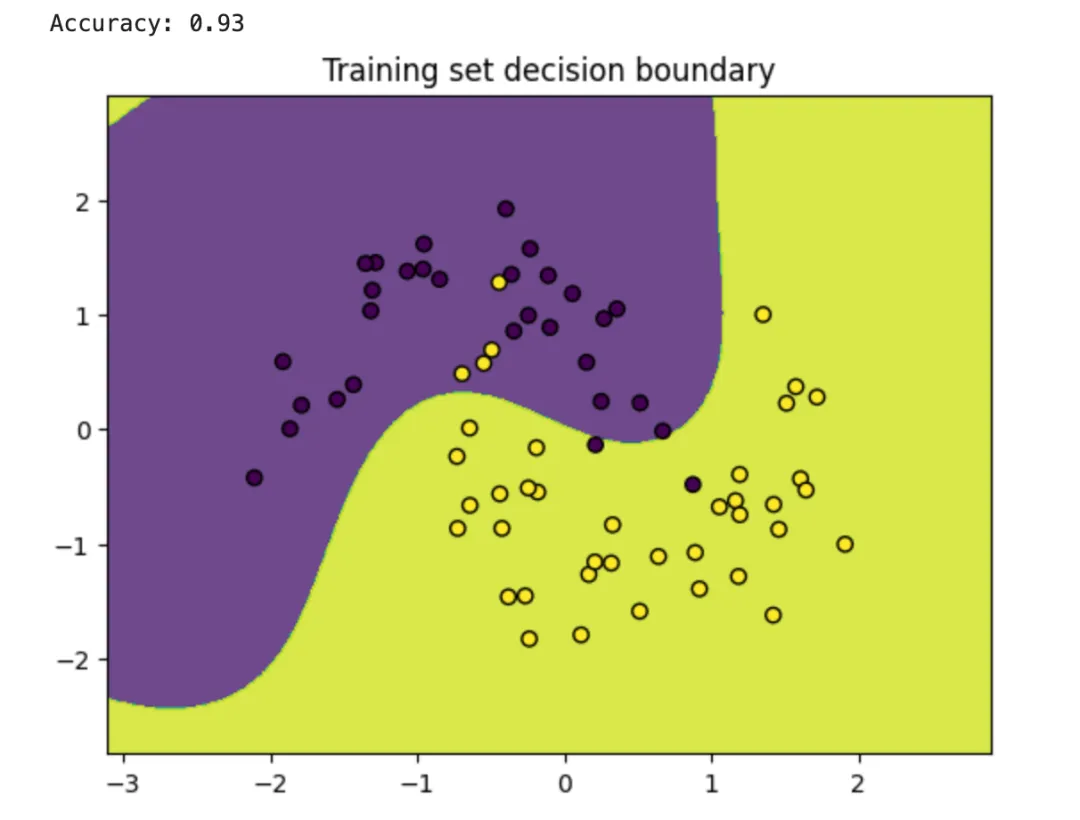
三、SVM回归
SVM回归(Support Vector Machine Regression,SVR)是什么?SVM回归是支持向量机在回归问题中的应用。
与SVM用于分类任务相似,SVR尽量使所有训练样本点都离决策边界(在回归问题中通常称为决策函数或回归函数)尽可能近,但允许有一定的偏差。
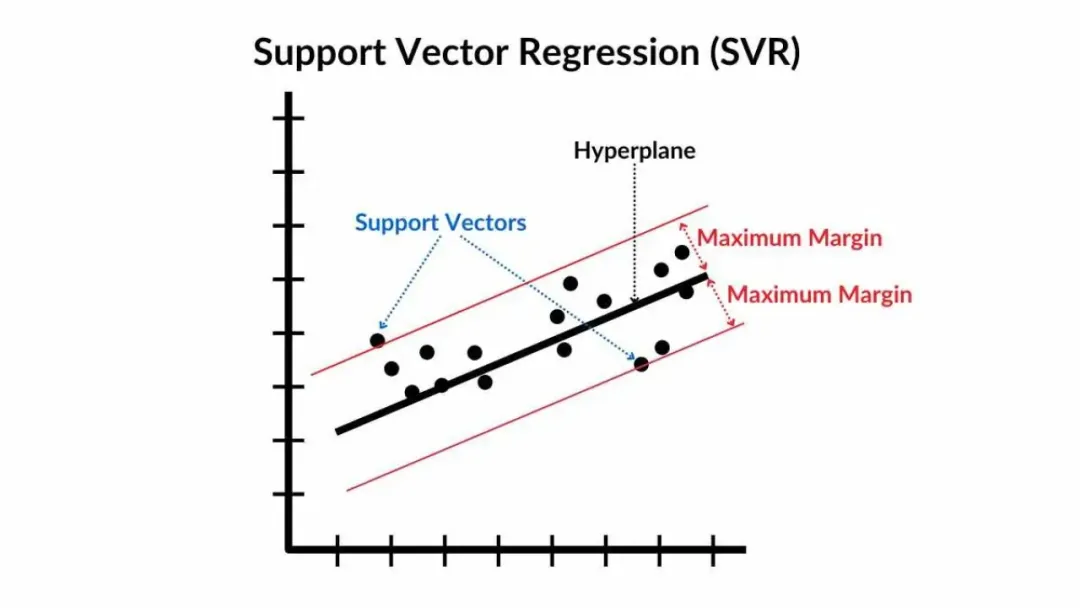
SVM回归如何实现回归任务?SVR通过寻找最优回归函数并允许一定误差范围,同时利用核函数和正则化参数来控制模型复杂度,以实现回归预测任务。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 生成一个回归数据集
X, y = make_regression(n_samples=100, n_features=1, noise=0.1, random_state=42)
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建SVR模型
svr = SVR(kernel='rbf', C=100, epsilnotallow=0.1)
# 训练模型
svr.fit(X_train, y_train)
# 使用模型进行预测
y_pred = svr.predict(X_test)
# 计算均方误差(MSE)作为评估指标
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")
# 可视化
# 在测试数据的范围内生成一系列点用于绘制回归线
X_plot = np.linspace(X.min(), X.max(), 1000).reshape(-1, 1)
y_plot = svr.predict(X_plot)
plt.scatter(X_train, y_train, color='blue', label='Training Data')
plt.scatter(X_test, y_test, color='green', label='Test Data')
plt.plot(X_plot, y_plot, color='red', label='SVR Regression Line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('SVR Regression')
plt.legend()
plt.show()本文转载自公众号架构师带你玩转AI 作者:AllenTang
















