一文彻底搞懂机器学习 - 逻辑回归（Logistic Regression）原创

鱼啊鱼

发布于 2024-12-6 10:20

浏览

0收藏

一文彻底搞懂机器学习 - 逻辑回归（Logistic Regression）-AI.x社区

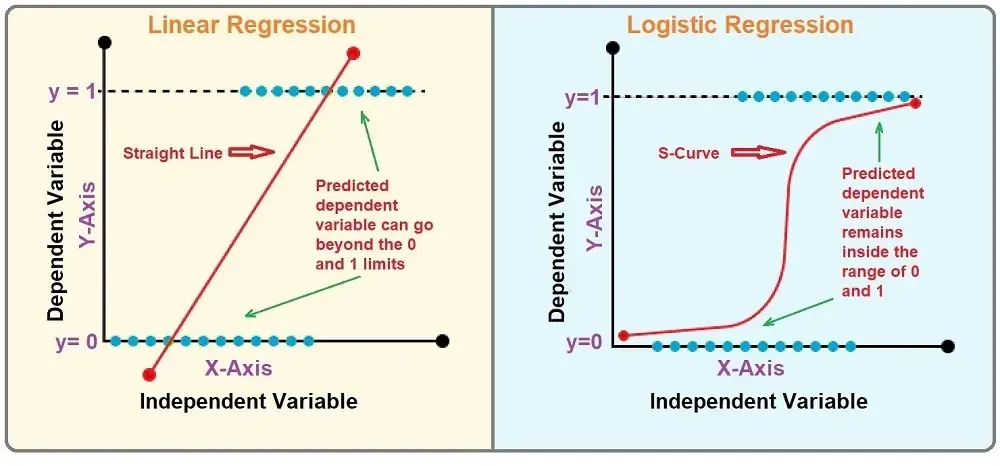
在机器学习中，逻辑回归（Logistic Regression）尽管名称中带有“回归”，但实际上是一种专为二分类问题设计的线性模型。

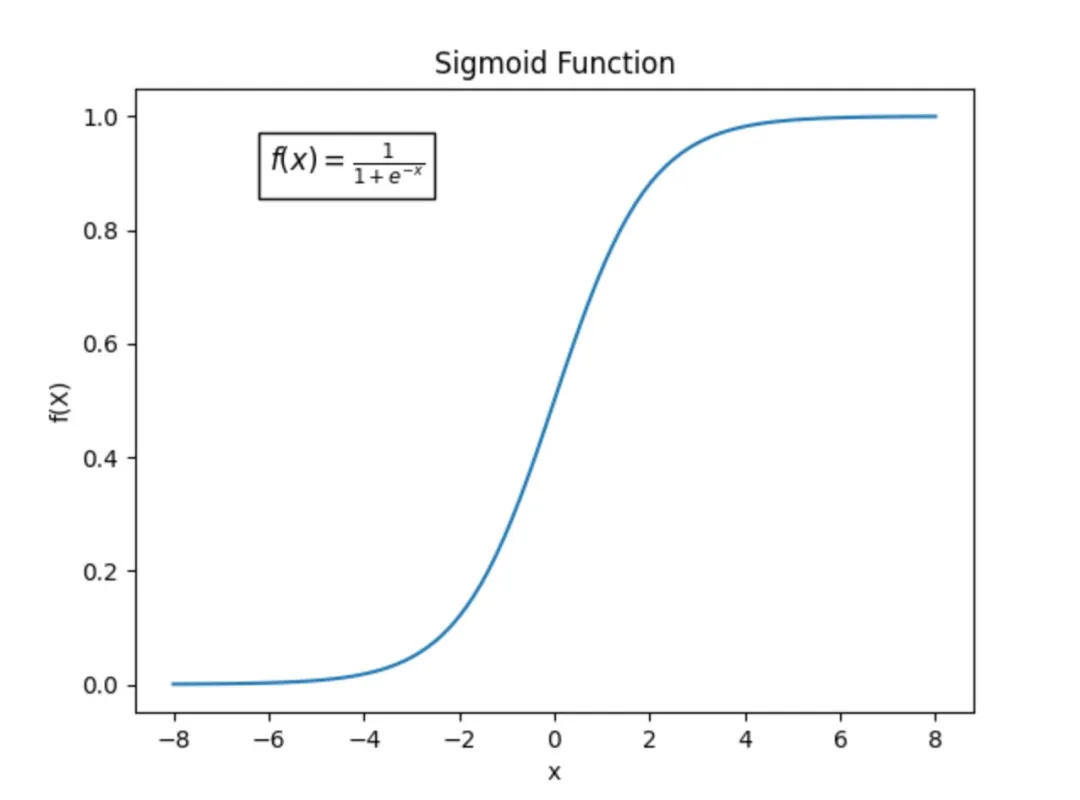
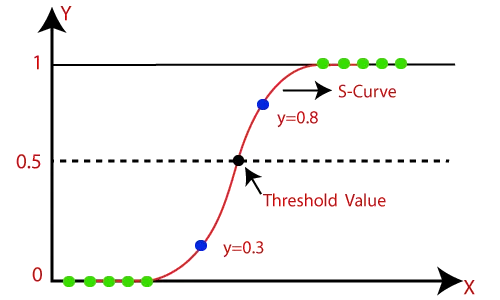
逻辑回归的实现基于线性回归模型，并在此基础上引入了sigmoid函数作为映射工具。Sigmoid函数的作用是将线性回归的输出（其值域原本为整个实数范围）巧妙地压缩至（0, 1）区间，从而该输出可以被解释为属于某一类别的概率。

一文彻底搞懂机器学习 - 逻辑回归（Logistic Regression）-AI.x社区

Logistic Regression

一、逻辑回归

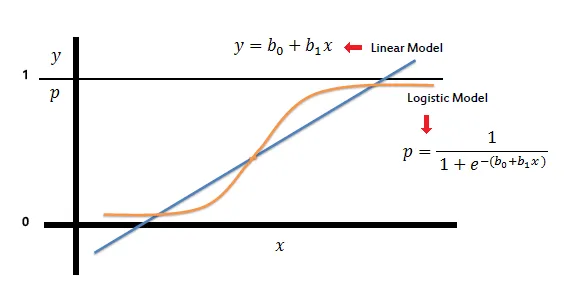
逻辑回归（Logistic Regression）是什么？逻辑回归是一种广泛用于二分类问题的线性模型，它的目标是找到一个函数，将输入特征映射到（0, 1）之间的概率值，以预测目标变量的分类。

一文彻底搞懂机器学习 - 逻辑回归（Logistic Regression）-AI.x社区

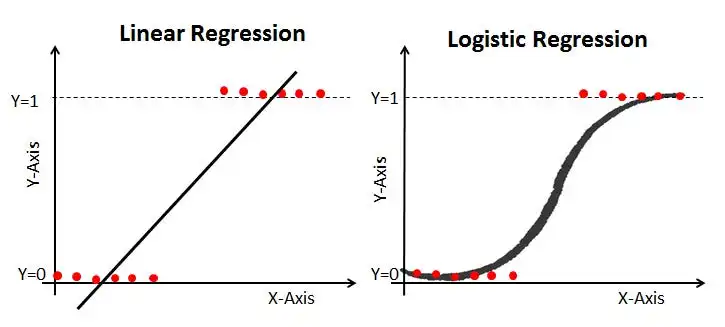
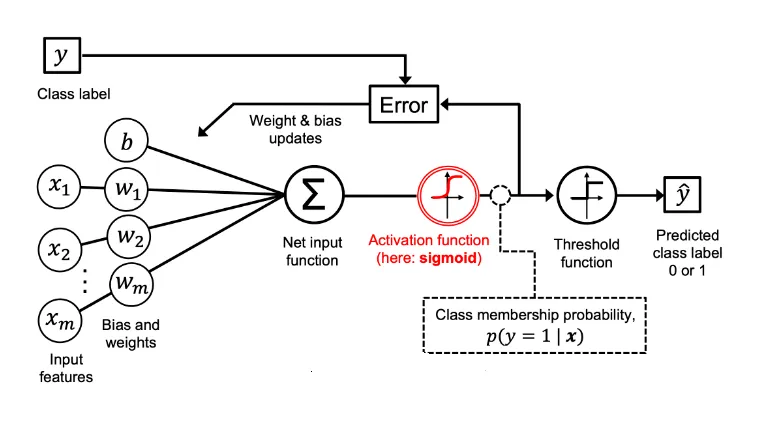
逻辑回归如何将输出映射到（0，1）？逻辑回归通过将线性回归模型的预测结果经过一个非线性函数——sigmoid函数进行变换，从而将输出映射到（0，1）之间。

逻辑回归如何进行训练？逻辑回归的训练过程包括准备数据、定义模型、构造损失函数、优化模型参数、评估模型性能和应用模型等步骤。通过迭代优化模型参数，逻辑回归可以找到最佳的分类边界，从而实现对数据的准确分类。

一文彻底搞懂机器学习 - 逻辑回归（Logistic Regression）-AI.x社区

逻辑回归使用对数似然损失函数来衡量模型的预测结果与实际标签之间的差异。为了找到最佳的模型参数θ，需要最小化损失函数J(θ)。这通常采用随机梯度下降法或批量梯度下降法来优化模型参数。

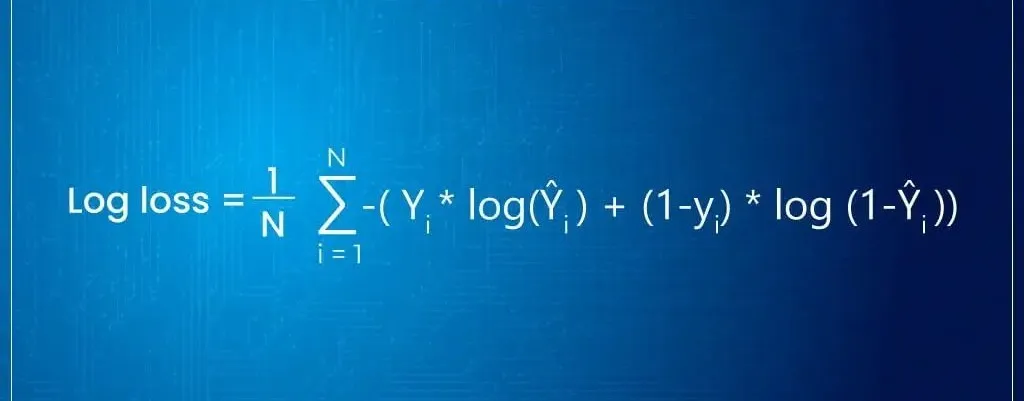
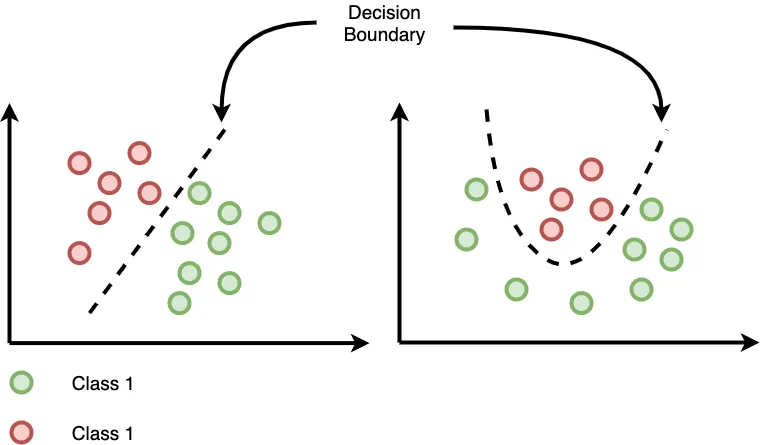
逻辑回归决策边界是什么？逻辑回归的决策边界是模型预测类别时所使用的分割超平面（在二维空间中为一条直线，三维空间中为一个平面，以此类推）。

逻辑回归模型通过线性函数计算出一个分数，然后使用sigmoid函数将这个分数转换为概率，最终根据设定的阈值（通常是0.5）来决定样本属于哪个类别。

一文彻底搞懂机器学习 - 逻辑回归（Logistic Regression）-AI.x社区

二、Pytorch实现逻辑回归

基于PyTorch实现逻辑回归模型并进行可视化涉及几个关键步骤：生成数据集、定义逻辑回归模型、初始化模型、损失函数和优化器、训练模型，以及绘制决策边界。

以下是一个简化的例子，展示如何使用PyTorch实现逻辑回归。

生成数据集：

生成一个二维数据集，其中 X 是输入特征，y 是标签（基于简单的线性决策边界）。

定义逻辑回归模型：

使用 nn.Linear 定义线性层，并使用 nn.Sigmoid 将输出转换为概率。

初始化模型、损失函数和优化器：

使用二元交叉熵损失（BCELoss）作为损失函数，使用随机梯度下降（SGD）作为优化器。

训练模型：

进行前向传播计算输出，计算损失，进行反向传播并更新模型参数。

绘制决策边界：

创建一个网格并预测每个点的类别，使用Matplotlib绘制决策边界和数据点。

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt


# 生成一个二维数据集
np.random.seed(0)
num_samples = 100
X = np.random.randn(num_samples, 2)
y = (X[:, 0] + X[:, 1] > 0).astype(int)  # 简单的线性决策边界


# 将数据转换为Tensor
X_tensor = torch.tensor(X, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.long)


# 定义逻辑回归模型
class LogisticRegression(nn.Module):
    def __init__(self, input_dim):
        super(LogisticRegression, self).__init__()
        self.linear = nn.Linear(input_dim, 1)
        self.sigmoid = nn.Sigmoid()
    
    def forward(self, x):
        out = self.linear(x)
        return self.sigmoid(out)


# 初始化模型、损失函数和优化器
input_dim = 2
model = LogisticRegression(input_dim)
criterion = nn.BCELoss()  # Binary Cross Entropy Loss
optimizer = optim.SGD(model.parameters(), lr=0.01)


# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    model.train()
    
    # 前向传播
    outputs = model(X_tensor).squeeze()
    labels = y_tensor.float()  # BCELoss需要浮点数标签
    
    # 计算损失
    loss = criterion(outputs, labels)
    
    # 反向传播和优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if (epoch+1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')


# 绘制决策边界
def plot_decision_boundary(model, X):
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
                         np.arange(y_min, y_max, 0.01))
    grid = np.c_[xx.ravel(), yy.ravel()]
    preds = model(torch.tensor(grid, dtype=torch.float32)).detach().numpy().ravel()
    
    plt.contourf(xx, yy, preds.reshape(xx.shape), alpha=0.8)
    plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o')
    plt.show()


# 绘制决策边界
model.eval()
with torch.no_grad():
    plot_decision_boundary(model, X)

一文彻底搞懂机器学习 - 逻辑回归（Logistic Regression）-AI.x社区