回复
深度学习故障诊断规则提取案例分析（可解释性）
案例使用的试验数据来源于常见的凯斯西储大学轴承数据中心，试验台采集的振动信号数据包括四种状态，分别是健康状态、内圈故障、滚动体故障、外圈故障。案例选择驱动端振动传感器采集的数据，采样频率为12000Hz，轴承信号为SKF6205。为简化试验，仅使用电动机负荷为0的振动信号，转速为1797r/min。为便于对注意力的分布进行解释，案例应用包络谱作为模型的输入。对于四种状态的轴承数据，使用滑窗选取55段信号，每段信号包含12000个点，也就是1秒的数据。随后计算段信号的包络谱，并把0到2000Hz的频率幅值作为样本输入到模型中进行训练，即输入维度为1×2000。80%的样本被用作训练集，其余样本为测试集。案例使用的模型是基础的Transformer网络，其内部的自注意力机制针对振动信号具备良好的可解释。
由于该数据集的四种故障是极易区分的，所以模型在测试集上的准确率为100%。本案例将注意力权重映射到输入振动信号生成热图，解释模型的决策依据。根据轴承关键频率的计算公式，案例中的转频、内圈故障频率、外圈故障频率和滚动体故障频率大致分别为30Hz、162Hz、108Hz和141Hz。
经模型训练后，在测试阶段可获取该模型对于49个正常样本、25个内圈故障样本、25个滚动体故障样本和25个外圈故障样本的诊断预测结果。经过频谱分析和归一化处理后，可获得5类特征属性，即：1/2转频(1/2X)、转频(X)、二倍频(2X)、三倍频(3X)和四倍频(4X)。经过数据离散化分析，5类属性的断点如下表所示。
属性离散化断点
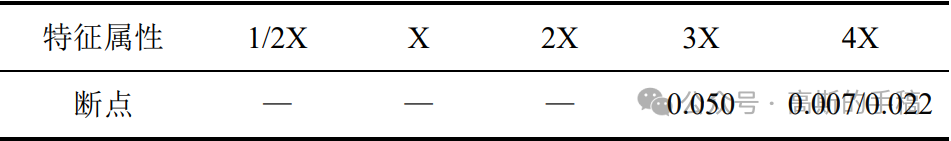
其中，三倍频(3X)的断点为0.050，表明该断点将此属性划分为两类。四倍频(4X)的断点为0.007和0.022，表明断点将该属性划分为小于0.007、0.008～0.022和大于0.022三类。不考虑其余属性对故障诊断的影响。因此，所提取的规则集如下表所示。
所提取的规则集
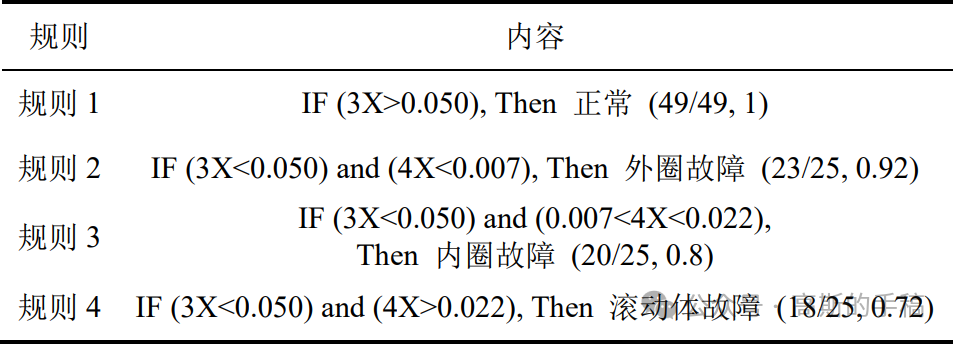
从上表可以看出，规则在一定程度上反映了外圈故障、滚动体故障和内圈故障的特征。其中，规则1表明正常样本的三倍频比故障样本的三倍频更为明显，49个示例样本全部满足该条规则，该规则的置信度为1。规则2表明，当样本的三倍频和四倍频皆较小时，为外圈故障。在25个示例样本中，共有23个样本满足该规则，置信度为0.92。规则3表明当三倍频较小、四倍频在0.007和0.022之间时，为内圈故障。在25个示例样本中，共有20个样本满足该规则，置信度为0.8。规则4表明当三倍频较小、而四倍频较大时，为滚动体圈故障。在25个示例样本中，共有18个样本满足该规则，置信度为0.72。该案例展示了规则提取方法可以将复杂模型学习到的难以解释的诊断知识转化为可解释的规则，提升了模型的可解释性。
知乎学术咨询：
https://www.zhihu.com/consult/people/792359672131756032?isMe=1担任《Mechanical System and Signal Processing》《中国电机工程学报》等期刊审稿专家，擅长领域：信号滤波/降噪，机器学习/深度学习，时间序列预分析/预测，设备故障诊断/缺陷检测/异常检测。
分割线分割线分割线
一维神经网络的特征可视化分析-以心电信号为例（Python，Jupyter Notebook）
包括Occlusion sensitivity方法，Saliency map方法，Grad-CAM方法
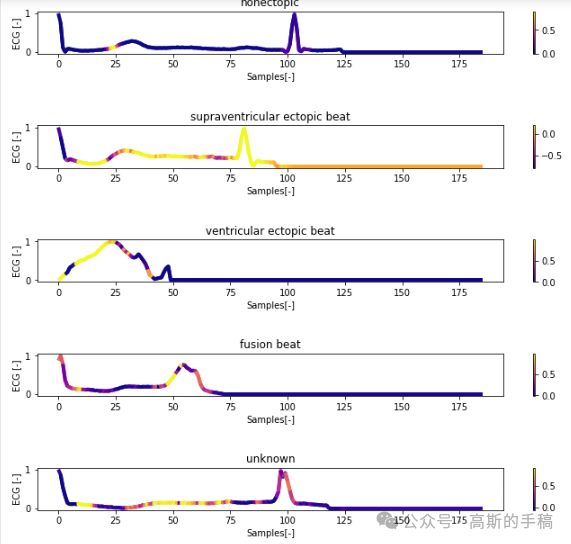
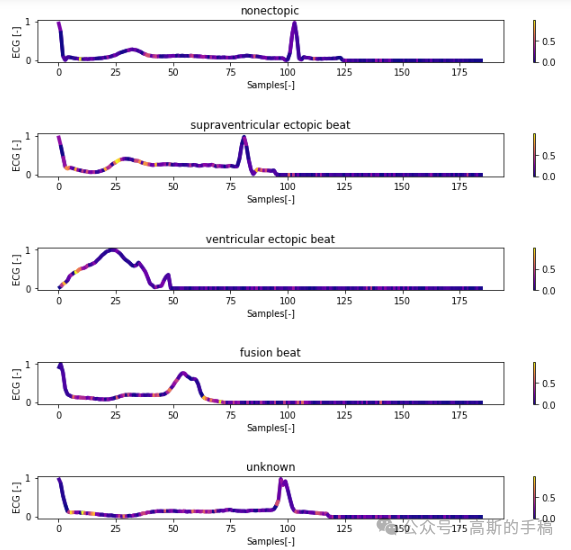
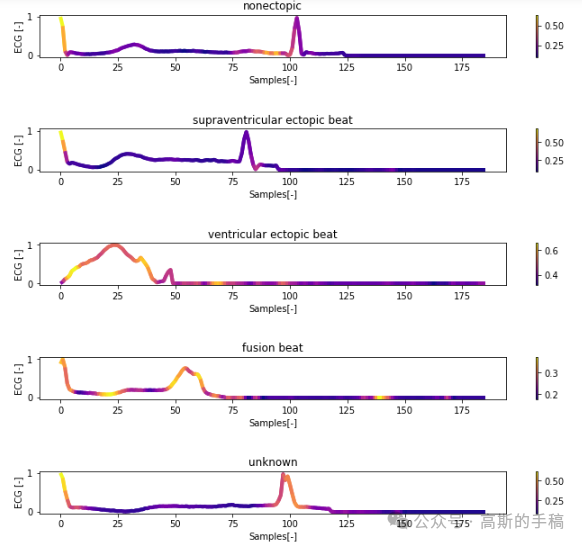
完整代码可通过知乎付费咨询获得：
https://www.zhihu.com/consult/people/792359672131756032基于深度学习的机械故障诊断及其权重可视化（Python）
完整代码可通过知乎付费咨询获得：
https://www.zhihu.com/consult/people/792359672131756032MATLAB环境下基于CNN的轴承故障诊断及特征可视化
算法程序运行环境为MATLAB R2021B，使用 CNN 进行滚动轴承故障诊断，原始数据来自西储大学轴承数据中心，包含3种故障工况（内圈故障，外圈故障和滚动体故障）和1种正常工况。
完整代码可通过知乎付费咨询获得：
https://www.zhihu.com/consult/people/792359672131756032医学图像的深度学习可解释性（MATLAB R2021B）
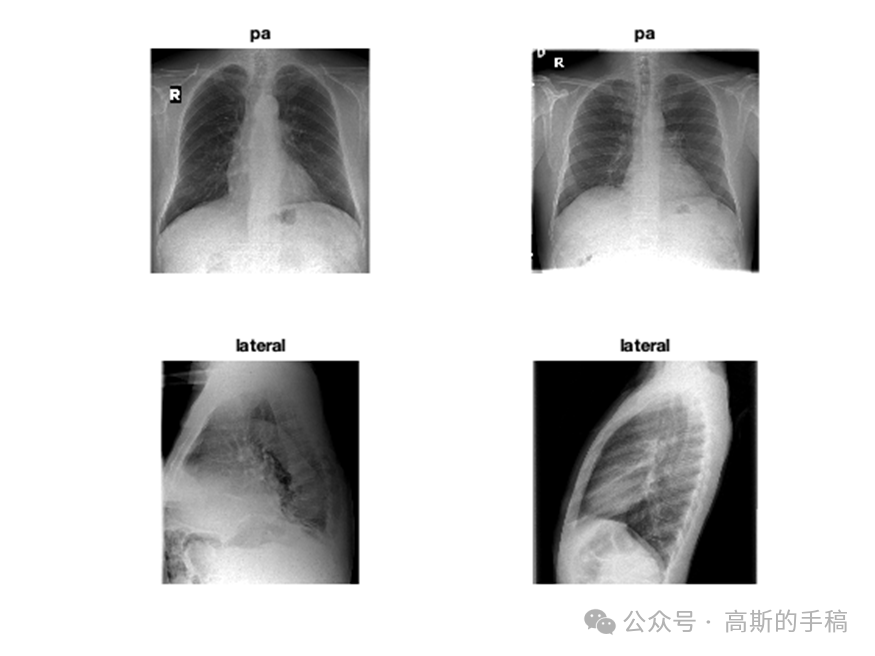
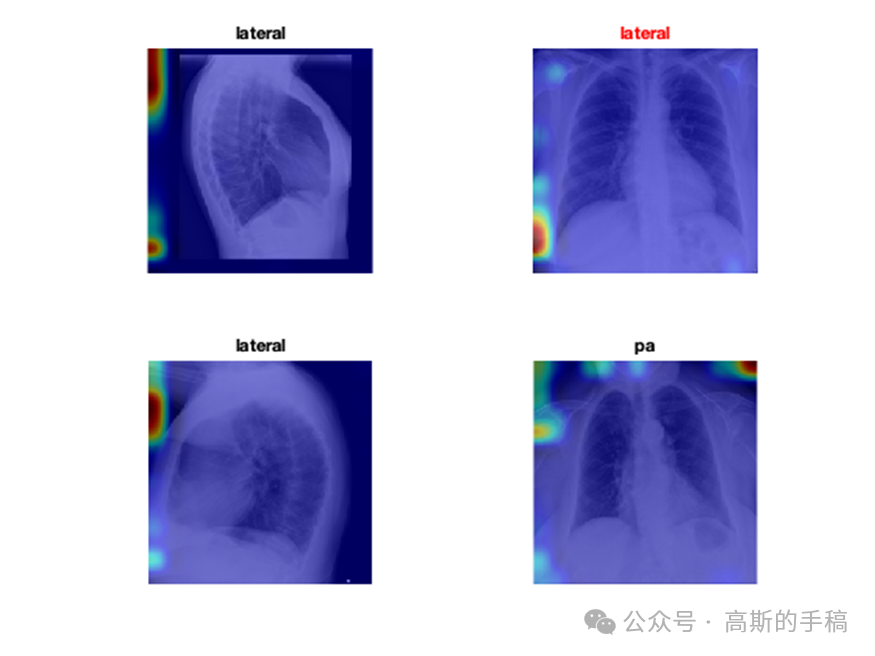
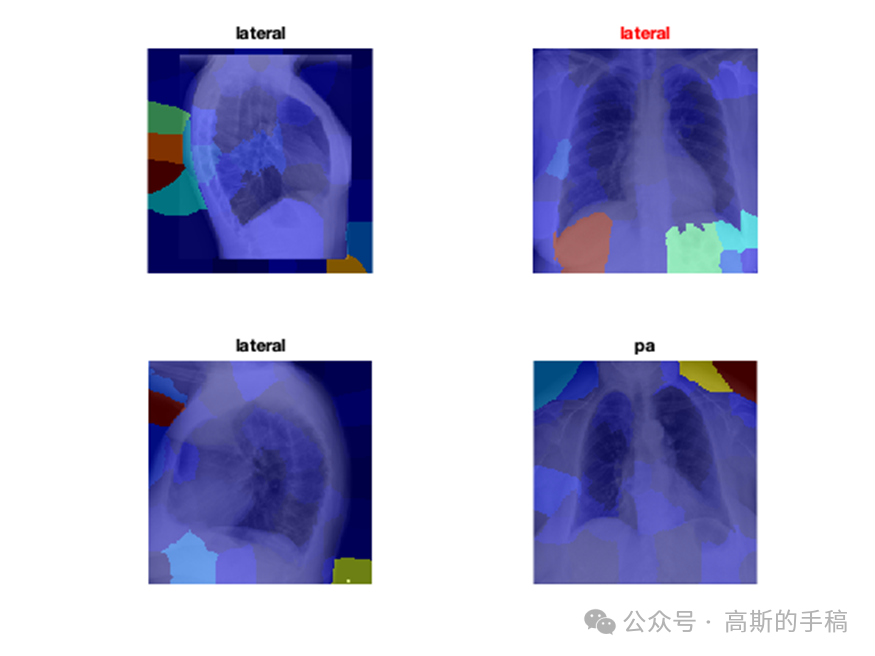
完整代码可通过知乎付费咨询获得：
https://www.zhihu.com/consult/people/792359672131756032一维时间序列信号的稀疏度度量方法（MATLAB R2018A）
算法运行环境为MATLAB R2018A，执行一维信号的稀疏度量方法，包括峰度(Kurt)、负熵(NE)、d -范数(DN)、2-范数与1-范数之比(L2/L1)、基尼指数(GI)、修正平滑指数(MSI)、基尼指数2 (GI2)、基尼指数3 (GI3)、广义基尼指数(GGI)、完全广义基尼指数等。
算法可迁移至金融时间序列，地震信号，机械振动信号，语音信号，声信号，生理信号（EEG,EMG）等一维时间序列信号。
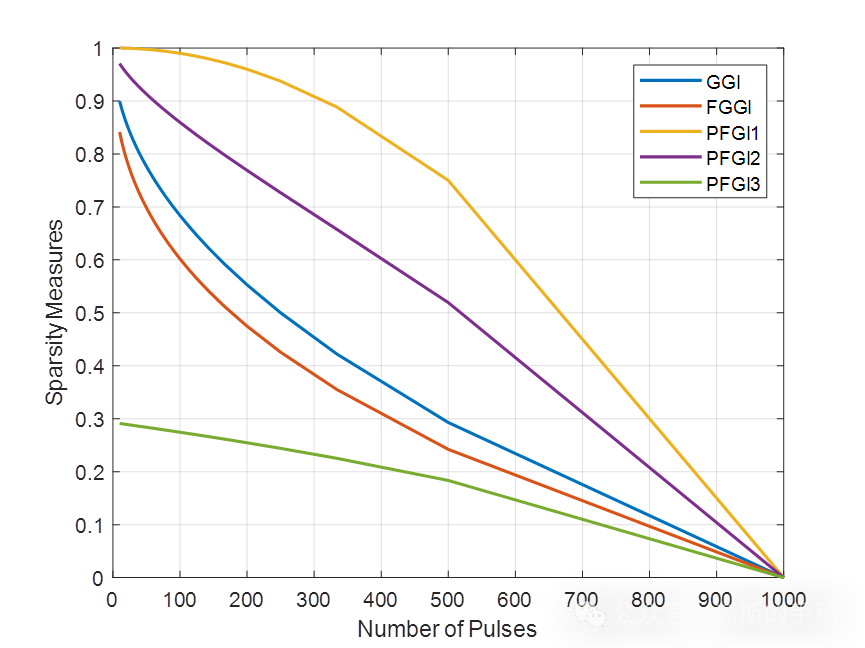
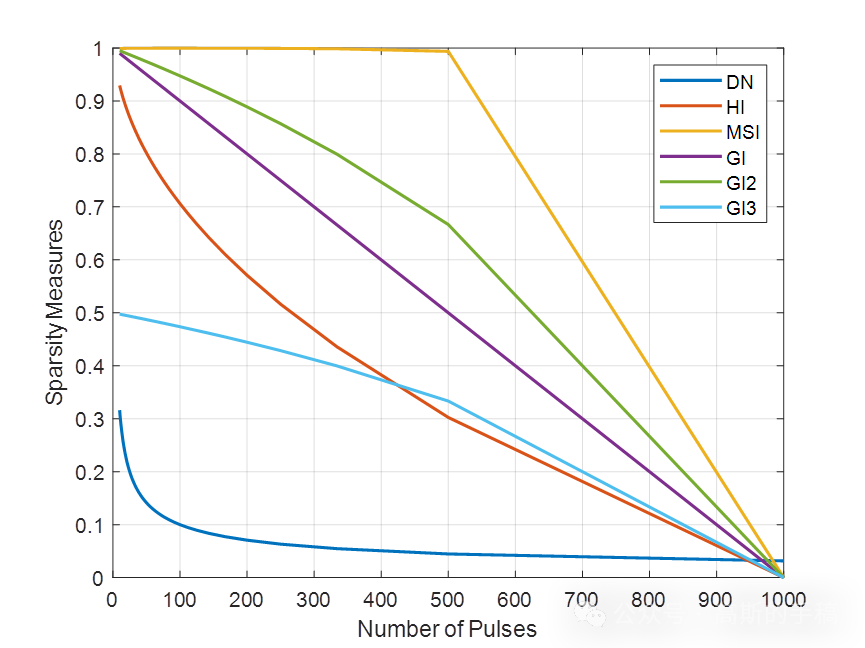
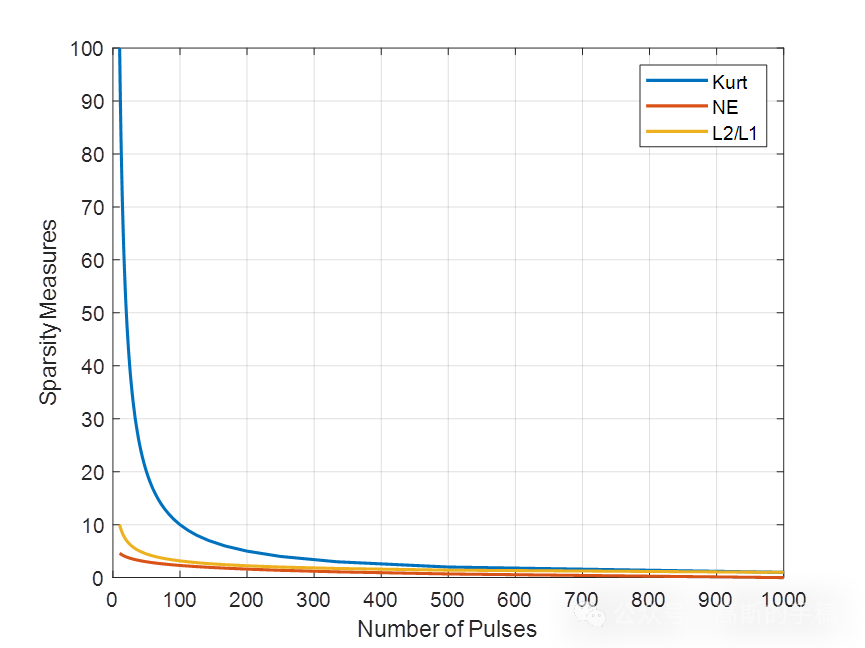
完整代码可通过知乎付费咨询获得：
https://www.zhihu.com/consult/people/792359672131756032分割线分割线
基于脉冲小波的旋转机械故障诊断（MATLAB R2018a）
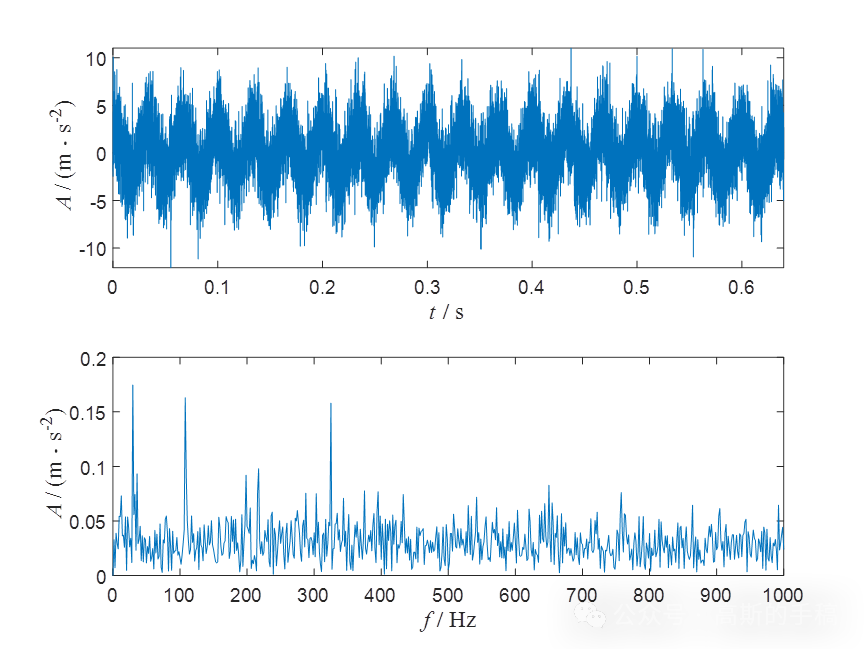
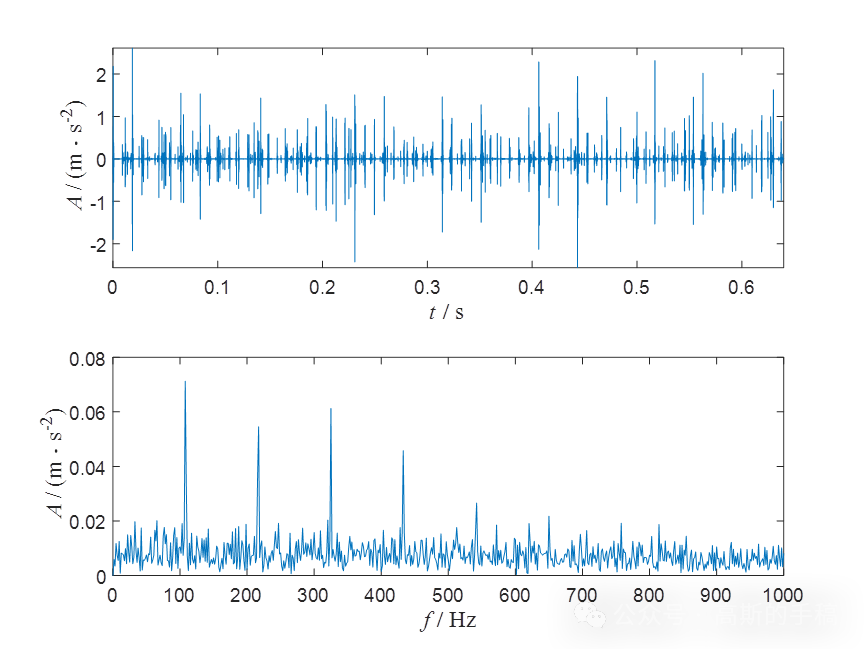
完整代码可通过知乎付费咨询获得：
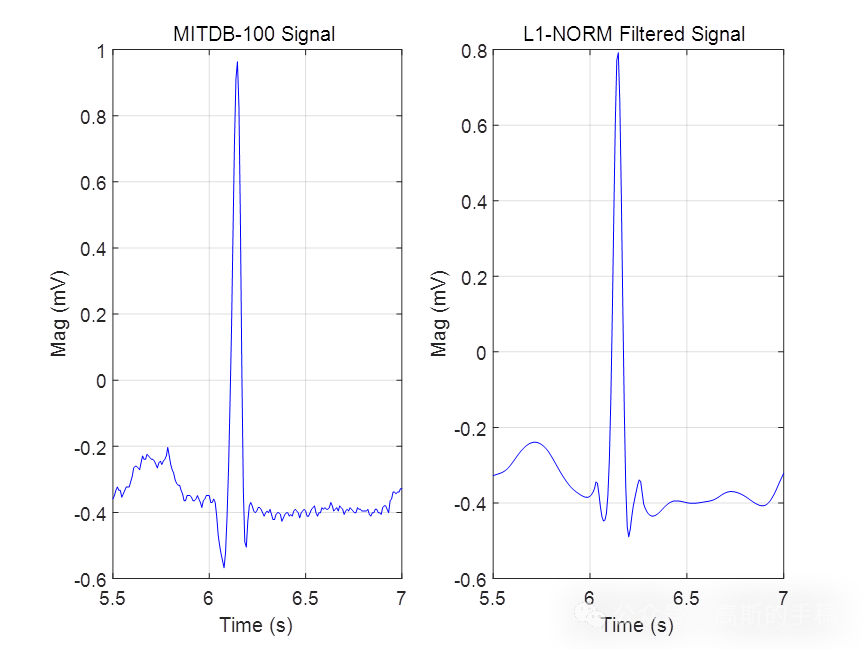
https://www.zhihu.com/consult/people/792359672131756032基于L1范数惩罚的稀疏正则化最小二乘心电信号降噪方法（Matlab R2021B）
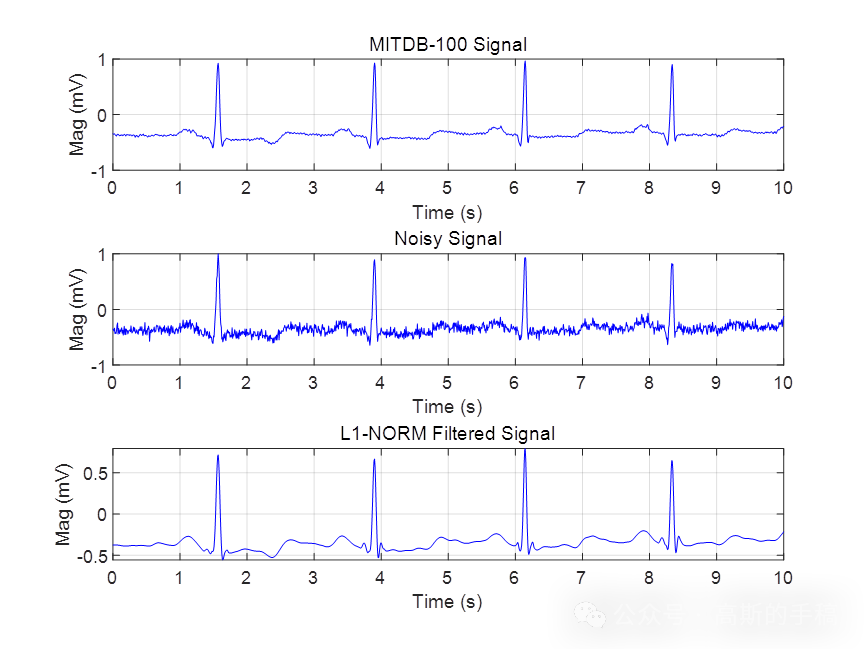
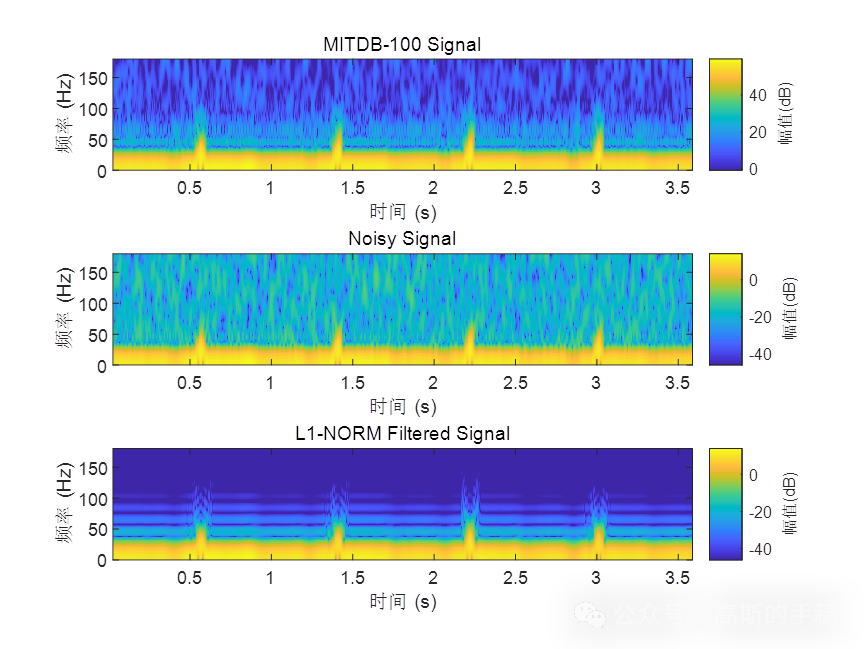
完整代码：
https://mbd.pub/o/bread/mbd-ZZaZmplr本文转载自高斯的手稿
赞
收藏
回复
相关推荐
