一文回顾常见图像融合方法
背景介绍
图像融合将多个源图像(可能来自不同传感器、不同视角、不同时间点)的信息整合到单一的输出图像中,这一过程旨在通过有效合并各源图像中的互补、冗余或独特信息,生成一个既包含所有关键细节又具有增强特性的综合图像。
例如对多帧不同曝光设置下的图像融合可以实现高动态范围(HDR)效果,对多帧不同焦段的图像进行融合可以得到大景深的图像,多张连续拍摄的相同环境下的图片可以有效降低图像中的噪点并提升整体画质,多个视角的图像拼接融合可以得到全景图像。

根据不同的融合任务需要设定不同的准则,然后对每张图像计算一个权重图。根据原始图像和融合权重图就可以根据融合算法计算结果。图像融合算法要保证结果过渡自然,清晰度不出现丢失。其余如色彩自然度、细节保留、边缘过渡、伪影抑制等方面也要尽善尽美。
常见的融合算法可以根据空间域融合和频域融合来划分:
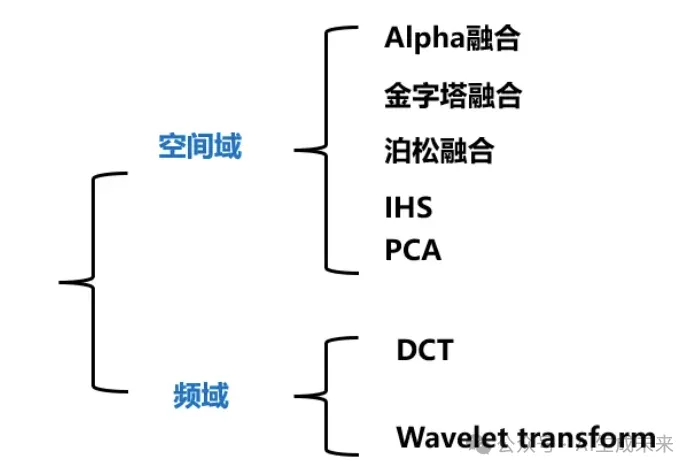
空间域融合
alpha融合
alpha融合作为最简单的融合方法,对于两张参与融合的图像每个对应位置的像直接进行加权,alpha控制各帧图像参与融合的比例。
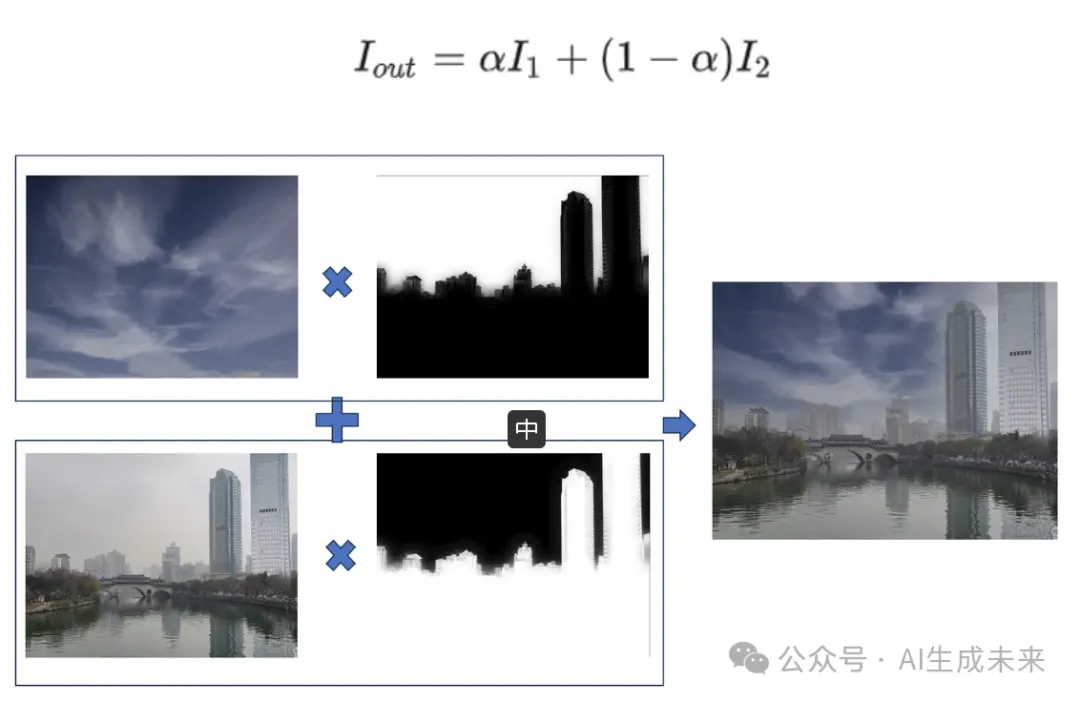
alpha融合适合在前景贴图、亮度比较接近的图像之间的拼接任务,alpha权重通常为物体的分割结果,并且为了过渡自然权重需要保持一定的平滑性。
金字塔融合
金字塔融合被广泛应用于多曝光融合任务中,对于不同亮度图像间的融合alpha融合很难保证融合mask边缘亮度过渡自然,金字塔融合利用图像金字塔结构来实现图像的多尺度融合,保证过渡平滑性。

金字塔融合主要涉及权重的高斯金字塔融合和图像的拉普拉斯金字塔融合,高斯金字塔是由同一幅图像经过一系列降采样和滤波操作构建而成的一组不同分辨率的集合,而拉普拉斯金字塔是高斯金字塔每个尺度的残差,那么图像就被分解为低分辨率下的低频分量和不同尺度下的高频细节。

对于每个尺度分别进行alpha融合得到该层融合结果,最后对融合结果的拉普拉斯金字塔做一次重建(当前层上采样叠加上一层)就可以得到融合结果。
泊松融合
图像泊松融合(Poisson Blending)是一种先进的图像编辑技术,主要用于将源图像中的某个物体或区域无缝地嵌入到目标图像中,创建出自然、无明显接缝的新图像。这一技术基于泊松方程及其在图像处理中的应用,特别适用于需要精确匹配源图像和目标图像之间光照、纹理和色彩的情况,以实现难以察觉的融合效果。

相较于Alpha融合,泊松融合对源图像融合边缘的精确性要求较低,不需要α mask精确的把物体贴边的截取出来,仍能实现较好的融合效果。
泊松融合的原理如下:v代表目标图像D的原始梯度场, g代表目标图像D的原始标量场(亮度),现在需要把目标图像这部分区域融进源图像S中,重建的融合结果我们设为f:
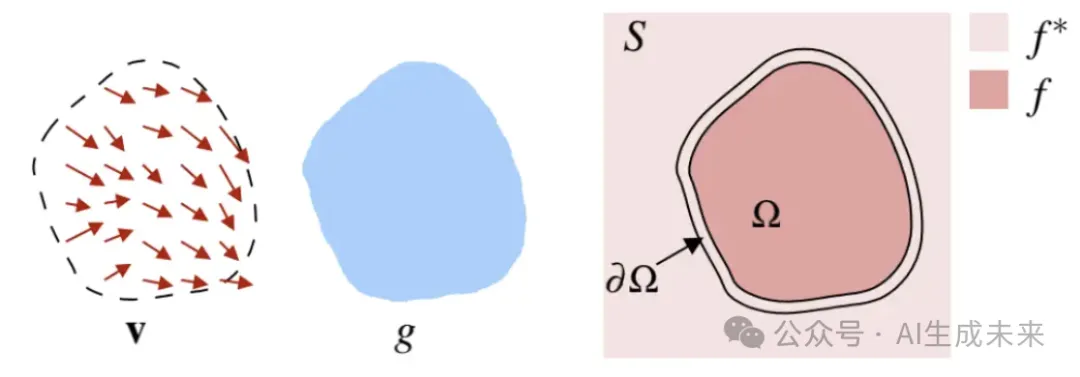
一方面我们希望f的结构信息(梯度)和目标图像D的梯度v不要有太大的变化,另一方面也希望f融合边界Ω的亮度和源图像S的边界亮度要相等,这样才能有一个平滑的过渡:
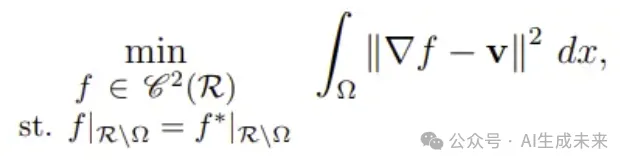
对于这个泛函方程的求解,带入欧拉-拉格朗日方程后,可以看成带有狄利克雷边界条件的泊松方程:
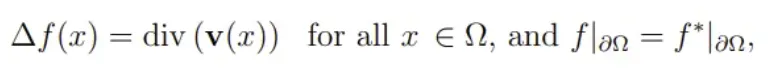
这里三角形代表亮度标量场的拉普拉斯算子,div代表梯度矢量场的散度。根据不同的需求散度可以直接等于目标图像D的散度,也可以对前后景D和S的散度做一些混合(mixed)。
补充材料:浅谈矢量场 -- 1.梯度、散度与拉普拉斯算子:https://blog.csdn.net/poisonchry/article/details/114387703
IHS融合
IHS融合(Intensity-Hue-Saturation Fusion)是一种主要用于遥感图像处理领域的图像融合技术,针对多光谱图像与高分辨率全色图像进行融合。其目的是结合多光谱图像丰富的光谱信息与全色图像的高空间分辨率,生成一幅既具有高空间细节又包含多光谱特征的融合图像。
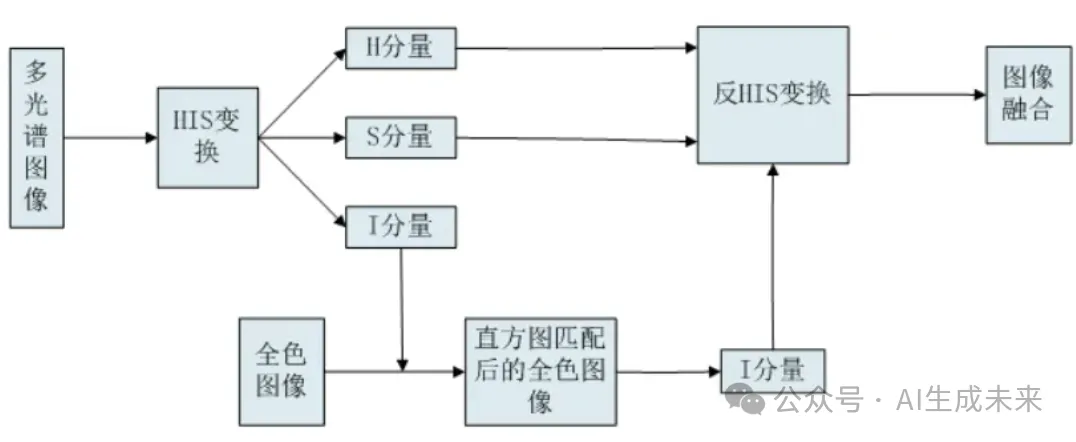
通过HIS变换将多光谱图像低空间分辨率的强度分量I和颜色成分H、S区分开,然后将全色图像高空间分辨率的强度分量替换过来,就可以得到一张色度和饱和度分量保持不变并且分辨率提升的图像。最后反HIS变换得到最终输出,即达到了空间分辨率的提升也对光谱信息和色彩做了保留。
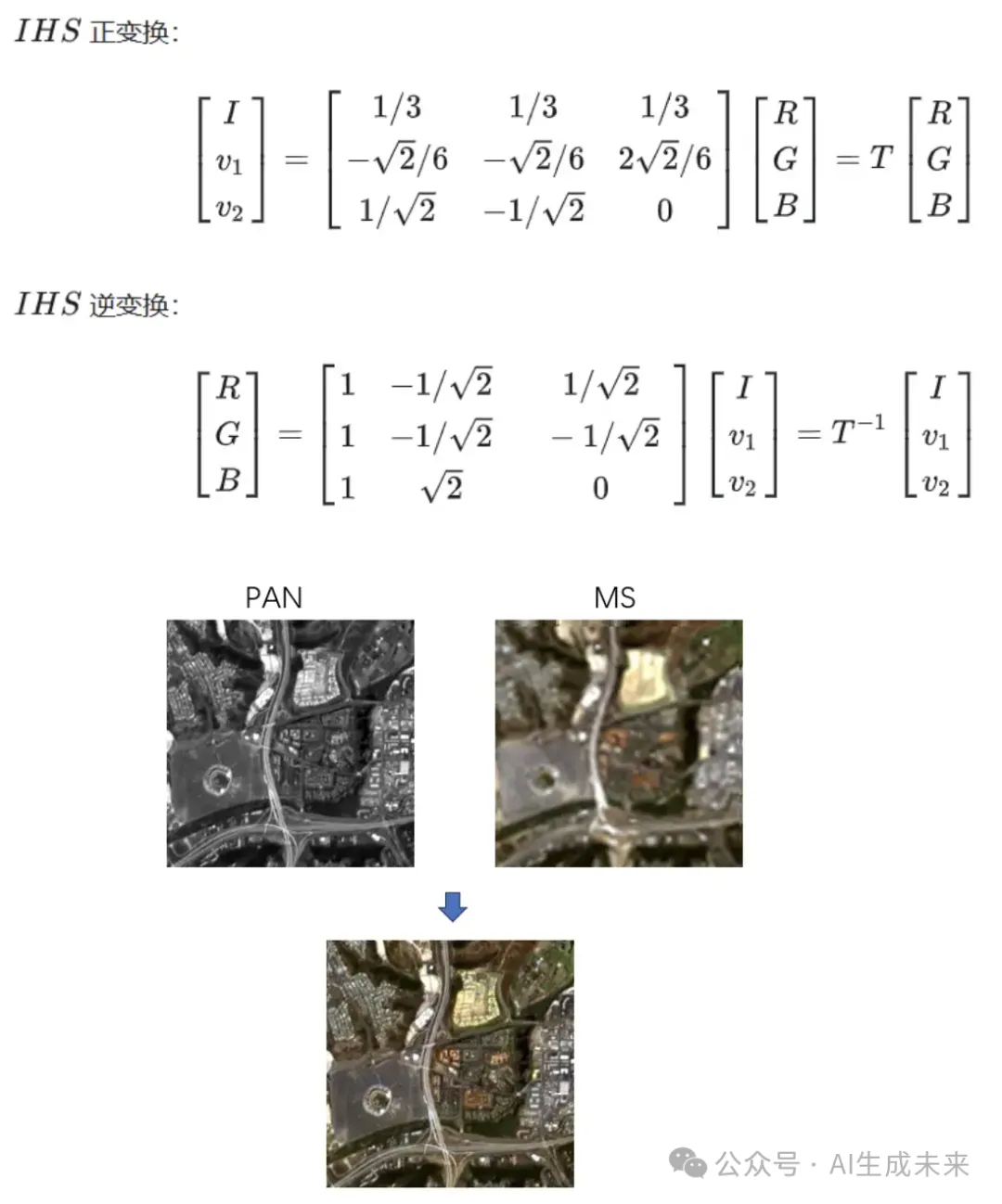
PCA融合
主成分分析(PCA)被广泛应用于数据降维,通过一组小于原始维度数量的基底P对原始数据X进行线性变换,将大量相关变量的信息浓缩到少数几个主成分中。其中每个主成分反映原始变量的大部分信息,特征值表示对应主成分所解释的原始数据的总方差比例。
PCA融合与IHS融合一样主要应用在遥感图像处理领域中,将具有不同特性的多光谱图像(高光谱分辨率、低空间分辨率)与全色图像(高空间分辨率、低光谱分辨率)结合起来,生成同时具备高空间分辨率和高光谱分辨率的融合图像。

实际处理中对于多光谱图像首先进行PCA分析,找出波段间协方差矩阵的主要特征向量(主成分),这些主成分代表了多光谱数据的主要变异方向,即光谱信息的主要组成部分。
对于全色图像将像素值(单波段)经过某种方式(如直方图匹配)调整,使其与多光谱图像的第一主成分(通常包含最多光谱信息)相匹配,使两者在光谱层面有一定的对应关系。
最后将调整后的全色图像(携带空间细节)与多光谱图像(携带光谱信息)按照某种规则(如加权平均、替换低频部分等)进行融合,生成最终的高空间分辨率、高光谱分辨率的融合图像。

补充材料:PCA主成分分析学习总结 (https://zhuanlan.zhihu.com/p/32412043),奇异值分解SVD(https://zhuanlan.zhihu.com/p/29846048)
频域融合
DCT融合
DCT变换将像素域的数据转换到频率域,频域中图像的能量主要集中在低频部分,高频部分则包含了更多的细节和边缘信息。我们可以利用多帧图像各自的频谱特性取长补短,提高图像的细节等部分。
图像分块:将输入的各帧图像分割成大小相同的子块。
DCT变换:对每个子块分别进行DCT变换转换到频率域。
融合规则:在DCT域内,通常依据各子块的频率特性进行融合操作,如高频信息融合保留图像的高频部分,因为其提供了更丰富的空间细节。低频信息融合根据图像的空间结构信息,通过加权、插值等方式融合低频部分。
逆DCT变换:A将融合后的DCT系数进行逆变换得到融合后的子块图像,并将所有融合后的子块拼接起来形成完整的融合图像。

在多景深合成任务中,融合准则设计为低频做平均、高频取最大值的策略,可以看到融合结果清晰度恢复效果比较好,并且也没有明显的块效应。
小波融合
小波分析能够同时捕获图像的频率和空间信息,使得在融合过程中能够有效地保留源图像的细节和结构特征。DWT 融合的基本步骤与DCT基本类似:首先对各帧图像进行小波变换,然后按照一定的融合准则对各帧的变换系数进行加权处理合并为一帧,最后对合并的单帧系数进行小波逆变换得到最后融合图像。
这里依然以多景深融合为例展示融合的过程,由于多景深融合需要取各帧清晰度高的地方,因此融合准则是取变换后系数的大数融合:

论文汇总
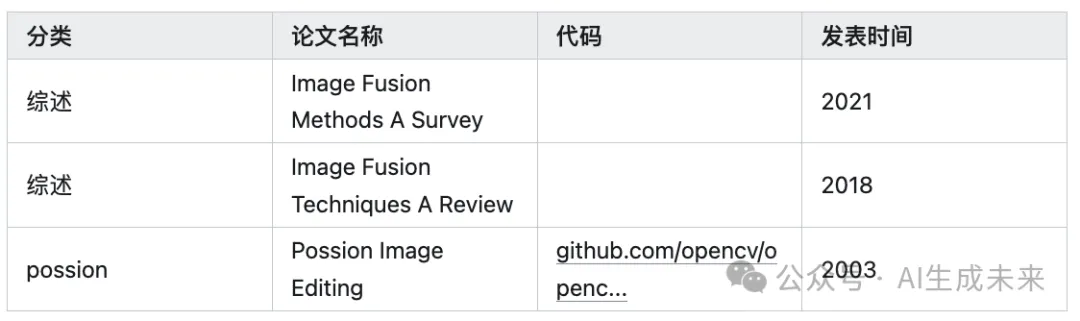
本文转自 AI生成未来 ,作者无关风月

















